Введение в теорию численных методов

Часть 1. ВВЕДЕНИЕ

Лекция 1

ВВЕДЕНИЕ В ТЕОРИЮ ЧИСЛЕННЫХ МЕТОДОВ

ЦЕЛЬ ЛЕКЦИИ: определить предмет курса; дать общую характерис­тику таких свойств численных методов как эффективность, точность, устойчивость, экономичность; пояснить эти свойства на простейших вычислительных правилах.

Основные требования, предъявляемые к вычислительным

алгоритмам

Вычислительный алгоритм должен быть устойчивым к ошибкам, обеспечивать требуемую точность, быть эффективным по времени выполнения, быть экономичным по требуемым объемам памяти, не допускать аварийных остановов. Поясним эти требования.

Устойчивость. Пусть последовательность величин вычисляется по рекурсивному правилу

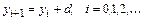
при заданных 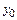и d.

Предположим, что при вычислении 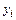внесена ошибка d_i (например, за счет операции округления), т. е. вместо значения 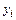использу-ется приближенное значение

.

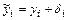В соответствии с рекурсивным правилом

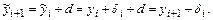
Следовательно,

и ошибка, допущенная на i-м шаге процесса, на следующем шаге не увеличивается, если операция сложения выполнена без новых округлений. Это означает, что алгоритм устойчив.

Рассмотрим другое рекурсивное правило вычисления этой последовательности:

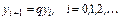
Опять y₀ и q считаем заданными.

Пусть, как и в предыдущем примере,

.

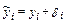Тогда

,

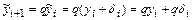или

.

В этом случае

,

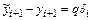и при ôqç>1 ошибка будет возрастать. Такой алгоритм является неустойчивым.

Точность. Обозначим через y точное решение задачи, y_k – ее приближенное значение, полученное на k-м шаге численного метода. Тогда

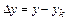
составляет погрешность решения, а

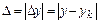
является абсолютной погрешностью.

Вычислительный алгоритм должен давать решение с заданной точностью и, следовательно, критерием завершения процесса уточнения решения является выполнение неравенства

.

На практике в силу трудностей вычисления абсолютной погрешности вместо D используют ее оценку сверху – предельную абсолютную погрешность Δ_y. В качестве Δ_y выбирают как можно меньшее значение, удовлетворяющее неравенству

,

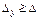а критерием завершения процесса в этом случае является неравенство

.

Часто используют относительную погрешность

т. е. абсолютную погрешность на единицу измерения, и предельную относительную погрешность

.

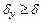Критерий завершения процесса в этом случае имеет вид

,

где 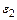– заданная допустимая относительная ошибка.

Рассмотрим в качестве примера, как может быть построена оценка предельной абсолютной погрешности вычисления значений функции

,

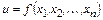если известны абсолютные погрешности ее аргументов.

Ошибка имеет вид

.

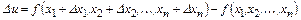Тогда

,

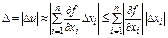и в качестве предельной относительной погрешности можно использовать величину

.

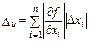Пусть решением задачи является вектор

,

который будем рассматривать как элемент векторного пространства 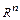. Приближенное решение

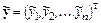
и его погрешность

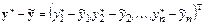
также являются элементами этого пространства. Рассмотрим, как оцениваются ошибки решения в этом случае. Для этого используем количественную характеристику вектора в виде нормы.

Говорят, что в задана норма, если каждому вектору 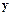из сопоставляется вещественное число , называемое нормой вектора 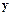, для которого справедливы следующие свойства:

1. 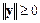, причем 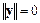тогда и только тогда, когда ,

2. 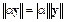для любого вектора 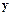и любого числа a,

3. 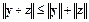для любых векторов 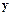и .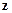

В вычислительных методах наиболее употребительны следующие нормы:

.

Абсолютную и относительную погрешность вектора в любой из перечисленных выше норм можно определить следующим образом:

.

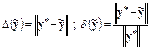Имеет смысл говорить об абсолютной и относительной погрешности (m´n)- матрицы решений A. В этом случае используется такая характеристика, как норма матрицы, согласованная с нормой вектора. Для нормы матрицы A, обозначаемой 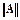,справедливы следующие свойства:

1. 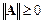, причем тогда и только тогда, когда ,

2. 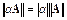для любой матрицы A и любого числа a ,

3. 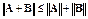для любых (m´n)-матриц 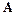и .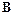

Каждой из векторных норм соответствует своя согласованная норма матриц. В частности, нормам 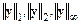соответствуют нормы 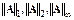, вычисляемые по правилам

где l_j(A^TA) – собственные числа матрицы A^TA.

Абсолютная и относительная погрешности матрицы решений вычисляются через соответствующие нормы:

,

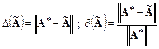причем 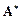– искомая матрица решений, 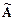– ее некоторое приближение.

Эффективность. Эффективность вычислительного алгоритма оценивают по времени реализации либо по общему числу операций, требуемых для получения результата.

Обозначим через n_сл число операций сложения, через n_у – число операций умножения, через n_дел – число операций деления, через t_у, t_дел, t_сл – время выполнения операций умножения, деления и сложения на ЭВМ. Объективный критерий сравнения вычислительных алгоритмов – требуемое время вычислений:

T=n_уt_у+n_слt_сл+n_делt_дел.

Если t_у≈t_дел≈t_сл, то T≈(n_у+n_дел+n_сл)t_оп, где t_оп – время выполнения на ЭВМ арифметической операции, и критерием оценки эффективности алгоритма может быть

n_Σ=n_у+n_дел+n_сл .

Если t_у≈t_дел>>t_сл, то критерий эффективности – число так называемых длинных операций n_дл=n_дел+n_у.

Пусть Q – критерий эффективности метода. Значение Q зависит от требуемой точности e. Из двух сравниваемых вычислительных алгоритмов решения задачи из них будет эффективнее тот, который при заданном значении ε характеризуется меньшим значением Q.

В качестве примера построим два алгоритма вычисления полинома n-й степени

.

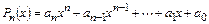Непосредственная реализация:

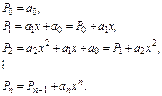
Расчет полинома по рекурсивному правилу

,

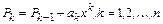вытекающему из приведенной реализации, соответствует алгоритму 1.

Алгоритм 1.

1. Начальная установка

2. Вычислить в цикле (k=1,2,…,n):

Алгоритм 1 характеризуется таким числом арифметических операций: nу=2n; nсл=n.

Преобразуем исходную запись полинома:

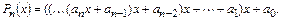
Теперь расчет полинома можно выполнить следующим образом:

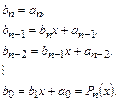
Записанное правило реализуется алгоритмом 2.

Алгоритм 2.

1. Начальная установка:

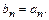
2. Вычислить в цикле (k=n,n-1,…,1):

Значение 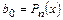. Затраты на выполнение алгоритма:

nу=n , nсл=n.

Очевидно, что алгоритм 2 эффективнее по времени выполнения алгоритма 1.

Экономичность. Экономичность алгоритма оценивается по требуемым для его реализации объемам памяти ЭВМ.

Аварийные остановы. Любое число ЭВМ принадлежит не всей числовой оси, а некоторому интервалу 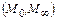. Если какое-либо число x в процессе работы алгоритма выходит за указанный интервал, то происходит так называемый аварийный останов. Необходимо построить вычислительный алгоритм таким образом, чтобы вычисленные в процессе его работы числа .