Как ведут себя материалы при испытании на сжатие?

Строительные материалы, такие как бетон и цемент, испытывают в основном на сжатие. Дерево испытывают на сжатие как вдоль, так и поперек волокон. Сталь испытывают на сжатие реже, чем на растяжение.

Образцы для испытания на сжатие имеют, как правило, форму кругового цилиндра с отношением высоты образца к диаметру не более 3.

Для стали марки Ст. 3 диаграмма сжатия вплоть до предела текучести полностью повторяет диаграмму растяжения, то есть 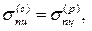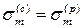. Различие начинает сказываться после наступления текучести. При этом площадка текучести при сжатии менее четко выражена, чем при растяжении.При больших деформациях различие становится особенно ощутимым, и в первую очередь из-за того, что сжатие сопровождается увеличением площади поперечного сечения образца, вследствие чего испытание требует постоянно возрастающей нагрузки.

Следовательно, при сжатии пластичного материала получить такую характеристику, как предел прочности, не представляется возможным. Исследуемый образец, не претерпевая разрушения, расплющивается, и дальнейшее испытание ограничивается возможностями пресса.

В расчетной практике предел прочности пластичного материала на сжатие условно принимается таким же, как и на растяжение.

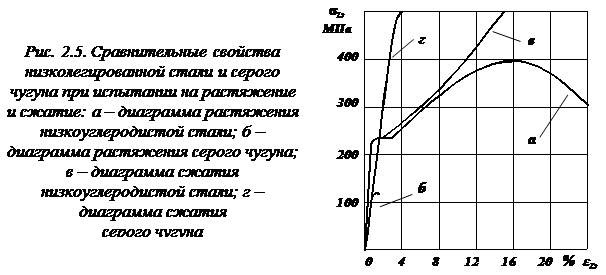
Диаграмма сжатия хрупкого материала по виду напоминает диаграмму растяжения, но предел прочности на сжатие, как правило, в несколько раз больше, чем на растяжение ( 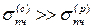). Разрушение образца при сжатии происходит обычно путем сдвига одной части относительно другой, происходящим примерно под углом 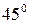к оси образца.

Наглядное представление о сравнительных механических характеристиках низкоуглеродистой стали и серого чугуна при растяжении и сжатии дают диаграммы, показанные на рис. 2.5.

2.18. Какое напряжение называется допускаемым? Как записывается условие прочности при растяжении и сжатии?

Испытания материала на растяжение и сжатие позволяют определить предельные напряжения 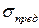, то есть те напряжения, при которых материал образца непосредственно разрушается или же в нем возникают большие пластические деформации.

Таким образом, в качестве предельного напряжения принимается:

· для пластичного материала – предел текучести (то есть считается, что разрушение пластичного материала начинается при появлении в нем заметных пластических деформаций):

;

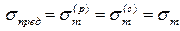· для хрупкого материала – предел прочности, значение которого при растяжении и сжатии различно: 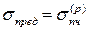или .

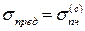Для обеспечения прочности реального стержня необходимо так выбрать его размеры и материал, чтобы наибольшее нормальное напряжение, возникающее в некоторой точке, было меньше предельного напряжения:

.

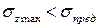Однако даже в том случае, когда наибольшее расчетное напряжение 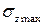в стержне будет близко к предельному напряжению, гарантировать его прочность еще нельзя. Дело в том, что внешние нагрузки, воздействующие на реальный стержень, не могут быть нами определены достаточно точно. Да и расчетные напряжения в стержне в ряде случаев могут быть вычислены лишь приближенно. Наконец, возможны отклонения действительных механических характеристик материала, применяемого для стержня, от характеристик, заложенных в расчете. Из сказанного следует, что стержень должен быть спроектирован с некоторым расчетным коэффициентом запаса прочности:

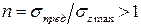. (2.6)

Ясно, что чем больше n, тем прочнее деталь. Однако совершенно очевидно, что очень большой коэффициент запаса прочности приводит к перерасходу материала и это делает стержень тяжелым и неэкономичным.

В зависимости от назначения конструкции и целого ряда других обстоятельств устанавливается допускаемый (или нормативный) коэффициент запаса прочности, который обозначается .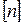

Прочность стержня считается обеспеченной, если 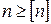. Это условие и называют условием прочности.

Используя выражение (2.6), перепишем условие прочности в виде:

.

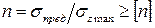Отсюда можно получить и другую форму записи условия прочности:

.

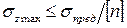Отношение предельного напряжения к допускаемому коэффициенту запаса прочности (то есть отношение, стоящее в правой части последнего неравенства) называется допускаемым напряжением. Оно обозначается 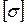и определяется по формуле

.

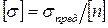В случае, когда предельные и соответственно допускаемые напряжения при растяжении и сжатии различны, их обозначают 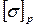и .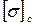

Пользуясь понятием допускаемого напряжения, можно условие прочности сформулировать следующим образом: прочность стержня будет обеспечена, если возникающее в нем наибольшее напряжение не превышает допускаемого напряжения.

Тогда окончательно условие прочности при растяжении (сжатии) записывается в следующем виде:

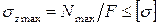. (2.7)

В случае, когда расчетное напряжение 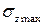получается значительно ниже допускаемого, площадь опасного поперечного сечения стержня должна быть уменьшена.

2.19. А что делать, когда расчетное напряжение незначительно,
но все же превышает допускаемое напряжение?

Такое незначительное превышение в расчетах на прочность допускается, но не более, чем на 5 %.

К сожалению, приходится констатировать, что студенты не всегда правильно понимают условие прочности (2.7). Так, на естественный вопрос, что произойдет со стержнем (конструкцией), если расчетное напряжение 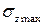превысит допускаемое напряжение 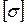, например, на 10 %, можно услышать ответ, что конструкция разрушится.

Это неверно. Она может и не разрушиться, если, например, выполняется условие, что 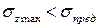. Еще раз подчеркнем, что допускаемое напряжение представляет собой долю от предельного напряжения.

Поэтому незначительное превышение расчетного напряжения над допускаемым напряжением означает лишь только снижение надежности конструкции. В этом случае расчетный коэффициент запаса прочности получается меньше допускаемого ( ).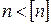

2.20. По какой формуле осуществляется подбор требуемой площади поперечного сечения стержня при растяжении (сжатии)?

Из неравенства (2.7) следует, что

.

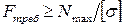2.21. В учебниках по сопротивлению материалов очень часто вместо термина «предельное напряжение» употребляется термин «опасное напряжение». Они одинаковы?

Предпочтение, на наш взгляд, следует отдать термину «предельное напряжение», которое и используется в настоящем пособии. И вот почему.

Слово «опасный» ассоциируется только с предупреждением о возможности или о большой вероятности разрушения и вовсе не означает, что оно уже началось или обязательно должно произойти. Но, если напряжение, например, достигло предела прочности, то нет никаких сомнений, что разрушение действительно началось. И это напряжение предельное, а не опасное.

2.22. А как записывается условие жесткости?

Оно имеет вид: 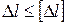, где 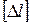– допускаемое удлинение стержня.

2.23. Что понимается под энергией упругой деформации при растяжении (сжатии) и чему она равна?

В науке под энергией понимается способность совершать работу.

При растяжении (сжатии) внешние силы совершают работу на перемещениях, которые получают точки их приложения в результате деформирования стержня. Вследствие этой работы, внутри тела накапливается потенциальная энергия деформации V. Последняя измеряется в системе СИ в джоулях (1 ДЖ = 1 Н·м). Один джоуль – это примерно потенциальная энергия яблока, находящегося на кухонном столе, по отношению к полу.

Энергию можно запасти, например, в пружине. Однако, как заметил Гук, поведение пружины является прототипом поведения деформируемого твердого тела при воздействии на него внешней нагрузки. Таким образом, любое деформирмируемое упругое тело является как бы аккумулятором энергии.

Потенциальная энергия деформации при растяжении (сжатии) определяется по формуле (подробнее см. беседу 15)

.

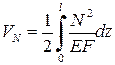2.24. Какие системы называются статически неопределимыми?

Системы, для которых не удается определить все опорные реакции из уравнений статики, называются статически неопределимыми.

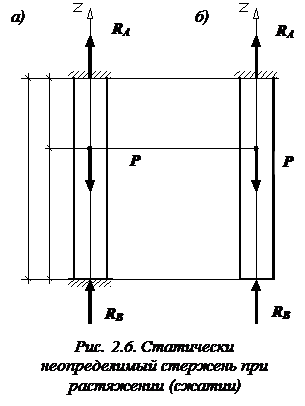
Рассмотрим, например, нагруженный стержень, заделанный обоими концами (рис. 2.6, а). В заделках возникают реакции, направленные вдоль оси стержня: 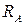и 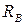. Для их определения мы имеем только одно уравнение статики:

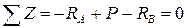. (2.8)

Назовем эту расчетную схему заданной системой (ЗС).

Для раскрытия статической неопределимости необходимо записать дополнительное уравнение. Это уравнение связано с деформацией ЗС и называется уравнением перемещений.

Поступим следующим образом. Отбросим, например, нижнюю заделку и действие отброшенной связи на стержень заменим некоторой реактивной силой 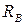, которую мы в дальнейшем будем рассматривать как активную силу (рис. 2.6, б). Полученный таким образом стержень назовем основной системой (ОС). Это название происходит от слова «основа» для дальнейшего расчета. Полученный нами стержень уже является статически определимым. Он заделан одним концом и нагружен двумя активными силами P и 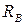. Правда, значение силы 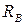мы пока не знаем.

Очевидно, что удлинение ЗС равно нулю, то есть 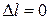. Поэтому неизвестную нам силу 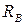мы можем найти из условия, что и удлинение ОС тоже равно нулю:

.

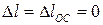Это уравнение и является тем самым дополнительным уравнением (уравнением перемещений), которое свидетельствует о том, что заданная и основная системы деформируются одинаково.

Используя принцип суперпозиции, запишем удлинение ОС в виде:

.

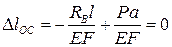Отсюда легко находим, что

.

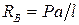Таким образом, статическая неопределимость нами раскрыта.

Вернемся к ЗС. Из уравнения (2.8) находим опорную реакцию :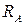

.

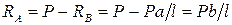Теперь мы можем перейти к построению эпюры продольных сил, определению напряжений и деформаций в стержне, оценке его прочности и жесткости.

2.25. Возникают ли в стержне напряжения при его нагреве или охлаждении?

Если при нагреве (охлаждении) стержня ничто не препятствует изменению его длины, то никаких напряжений в нем не возникает.

При нагреве линейные размеры тела увеличиваются, а при охлаждении – уменьшаются. Абсолютное удлинение стержня, вызванное изменением его температуры на 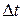градусов Цельсия, определяется по формуле

,

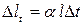где 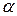– коэффициент линейного расширения материала стержня, а l – его длина.

Для стали, например, коэффициент линейного расширения примерно равен 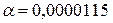. Если стальной стержень с первоначальной длиной 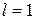м равномерно нагреть на 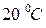, то его длина увеличится на 0,23 мм.

Иная картина имеет место для статически неопределимого стержня.

Предположим, что мы нагреваем стержень, жестко защемленный по концам (см., например, рис. 2.6, а ( 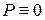)). Стержень хотел бы удлиниться на величину 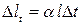, но этому препятствуют заделки. В них возникают реактивные силы 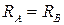, которые в итоге приводят к сжатию стержня.

Таким образом, при нагреве (охлаждении) статически неопределимого стержня в нем всегда возникают напряжения, которые принято называть температурными напряжениями.

Определим температурные напряжения 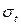в рассмотренном нами случае. Отбросим мысленно нижнюю заделку и действие отброшенной связи на стержень заменим реактивной силой 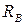(см. рис. 2.6, б ( 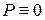)). Удлинение стержня 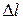, равное нулю, может быть представлено в виде

.

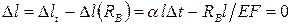Отсюда

.

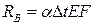Тогда температурные напряжения в стержне равны

.

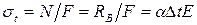2.26. Следует ли учитывать собственный вес стержня при растяжении и сжатии?

Знакомясь выше с теорией растяжения и сжатия стержня, мы пренебрегали влиянием его собственного веса. Дело в том, что при тех значительных внешних нагрузках, с которыми приходится сталкиваться при расчете реального стержня относительно небольшой длины, увеличение напряжения в нем за счет собственного веса в процентном выражении весьма невелико и поэтому собственный вес такого стержня действительно можно не учитывать.

Другую картину мы будем наблюдать при расчете очень длинных стержней, например, канатов, применяемых для подъема руды, или штанг насосов, используемых для откачивания воды в рудниках. Здесь собственный вес стержня уже будет играть большую роль.

Рассмотрим жестко закрепленный верхним концом стержень длиной 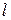и площадью поперечного сечения F. Пусть вес единицы объема материала стержня (удельный вес) равен 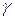. Тогда вес всего стержня .

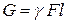Наибольшие нормальные напряжения, которые возникнут в поперечном сечении стержня вблизи заделки, будут равны

.

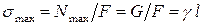Из условия прочности 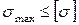можно определить предельную длину стержня:

.

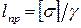Рассмотрим, например, пеньковый канат, удельный вес которого 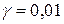мН/м³. При допускаемом напряжении 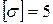МПа предельная длина получается равной:

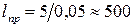м.

Как известно, глубина многих рудников бывает гораздо больше полученного значения.

Иногда определяют не предельную, а так называемую разрывную длину стержня:

,

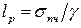где 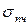– предел прочности.

Например, для каната, изготовленного из стали марки Ст. 3 с пределом прочности 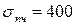МПа и удельным весом 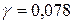МН/м³, получи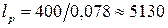м:

м.

2.27. Правильно ли говорить, например, «загрузить стержень такой-то нагрузкой», «загруженный элемент» и т. п.?

Действительно, в устной речи, а иногда в учебной и технической литературе можно встретить подобные или иные выражения. Однако эти выражения, конечно же, неправильные. Загрузить можно какую-либо емкость, например «загрузить вагон». Правильно говорить «нагрузить стержень», «нагруженный элемент» и т. д.

3. СДВИГ

Если деформация растяжения возникает, когда стержень тянут, а сжатия – когда его сдавливают, то деформация сдвига происходит тогда, когда его пытаются, например, разрезать ножницами. Сдвиг и будет темой нашей третье беседы. Вследствие сдвига разрушаются сварные и болтовые соединения, дают течь корабли, шатаются столы и т. п.

3.1. Что такое сдвиг? Какие внутренние усилия возникают в поперечных сечениях стержня при сдвиге?

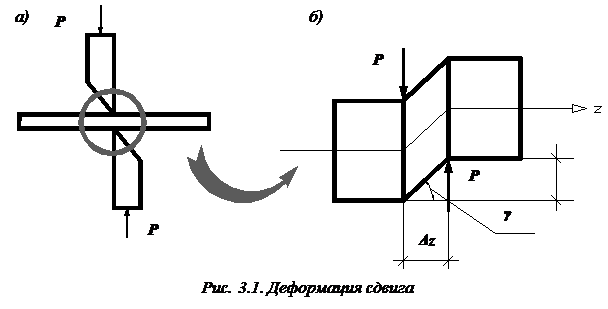
Сдвигом называется такой вид деформации, при котором одна часть стержня смещается относительно другой (как скользят, например, карты в колоде). Деформация сдвига будет происходить, например, в том случае, если к стержню приложить две равные по значению и противоположно направленные силы P, перпендикулярные к его оси z (рис. 3.1, а). Расстояние между этими силами 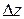должно быть очень малым, чтобы моментом 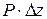, создаваемым этими силами, можно было пренебречь.

Применив метод сечений (разрезав стержень между силами P), можно легко установить, что в поперечном сечении стержня возникает только одно внутреннее усилие – поперечная (перерезывающая) сила .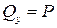

Далее мы увидим, что сдвиг возникает и при кручении стержня.

3.2. Что называется абсолютным сдвигом и углом сдвига (относительным сдвигом)?

В результате деформации сдвига одно поперечное сечение стержня смещается относительно другого на некоторую величину 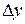, называемую абсолютным сдвигом.

Малый угол 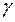, на который изменится первоначально прямой угол (рис. 3.1, б), называется углом сдвига или относительным сдвигом. Угол сдвига выражается в радианах.