Сортировка простым обменом
Классификация методов сортировки не всегда четко определена. Оба представленных ранее метода можно рассматривать как сортировку обменом. Однако существует метод, в котором обмен двух элементов является основной характеристикой процесса. Приведенный ниже алгоритм сортировки простым обменом основан на принципе сравнения и обмена пары соседних элементов до тех пор, пока не будут рассортированы все элементы.
Как и в предыдущих методах простого выбора, мы совершаем повторные проходы по массиву, каждый раз просеивая наименьший элемент оставшегося множества, двигаясь к левому концу массива. Если для разнообразия мы будем рассматривать массив, расположенный вертикально, а не горизонтально, и при помощи некоторого воображения представим себе элементы пузырьками в резервуаре с водой, обладающими «весами», соответствующими их ключам, то каждый проход по массиву приводит к «всплыванию» пузырька на соответствующий его весу уровень. Этот метод широко известен как сортировка методом пузырька.
procedure bubblesort:
var i,j: index;
x : item;
begin
for i:=1 to n do begin
for j:=n downto i do
if a[j - 1].key > a[j].key then begin
x:=a[j - 1];
a[j - 1]:=а[j];
a[j]:=x;
end
end
end; {bubblesort]
| Начальные ключи | i=2 | i=3 | i=4 | i=5 | i=6 | i=7 | i=8 |
Этот алгоритм легко оптимизировать. Этот пример показывает, что три последних прохода никак не влияют на порядок элементов, поскольку те уже рассортированы. Очевидный способ улучшить данный алгоритм – это запоминать, производился ли на данном проходе какой-либо обмен. Если нет, то это означает, что алгоритм может закончить работу. Этот процесс улучшения можно продолжить, если запоминать не только сам факт обмена, но и место (индекс) последнего обмена. Ведь ясно, что все пары соседних элементов с индексами, меньшими этого индекса k, уже расположены в нужном порядке. Поэтому следующие проходы можно заканчивать на этом индексе, вместо того чтобы двигаться до установленной заранее нижней границы i. Однако, если внимательней присмотреться, можно заметить странную асимметрию: один неправильно расположенный «пузырек» в «тяжелом» конце рассортированного массива всплывет на место за один проход, а неправильно расположенный элемент в «легком» конце будет опускаться на правильное место только на один шаг на каждом проходе.
Например, массив
12 18 42 44 55 67 94 06
будет рассортирован при помощи метода пузырька за один проход, а сортировка массива
94 06 12 18 42 44 55 67
потребует семи проходов. Эта неестественная асимметрия подсказывает третье улучшение: менять направление следующих один за другим проходов. Мы назовем полученный в результате алгоритм шейкер-сортировкой.
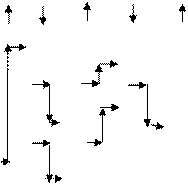 I=2 I=2 | ||||
| R=8 | ||||
procedure shakersort;
var j,k,l,r : integer;
x: item;
begin
l := 2; r := n; k:= n;
repeat
for j:=r downto l do
if a[j - 1].key > a[j].key then begin
x := a[j - 1];
a[j-1] := a[j];
a[j] := x;
k := j;
end;
l := k + 1;
for j := l to r do
if a[j - 1].key > a[j].key then begin
x := а[j - 1];
a[j - 1] := a[j];
a[j] := x;
k:=j;
end ;
r := k - 1;
until l > r;
end; {shakersort}
Анализ сортировки методом пузырька и шейкер-сортировки. Число сравнений в алгоритме простого обмена равно 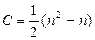 , а минимальное, среднее и максимальное количества пересылок (присваивание элементов) равны
, а минимальное, среднее и максимальное количества пересылок (присваивание элементов) равны 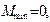
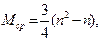
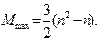
Анализ улучшенных методов, особенно метода шейкер-сортировки, довольно сложен. Наименьшее число сравнений есть 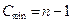 . Для усовершенствованного метода пузырька Д. Кнут получил, что среднее число проходов пропорционально
. Для усовершенствованного метода пузырька Д. Кнут получил, что среднее число проходов пропорционально 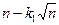 и среднее число сравнений пропорционально
и среднее число сравнений пропорционально 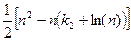 . Но мы замечаем, что все предложенные выше усовершенствования никоим образом не влияют на число обменов; они лишь уменьшают число избыточных повторных проверок. К сожалению, обмен двух элементов – обычно намного более дорогостоящая операция, чем сравнения ключей, поэтому все наши усовершенствования дают значительно меньший эффект, чем можно было бы ожидать.
. Но мы замечаем, что все предложенные выше усовершенствования никоим образом не влияют на число обменов; они лишь уменьшают число избыточных повторных проверок. К сожалению, обмен двух элементов – обычно намного более дорогостоящая операция, чем сравнения ключей, поэтому все наши усовершенствования дают значительно меньший эффект, чем можно было бы ожидать.
Анализ показывает, что сортировка обменом и ее небольшие улучшения хуже, чем сортировка включениями и выбором, и действительно, сортировка методом пузырька вряд ли имеет какие-то преимущества, кроме своего легко запоминающегося названия. Алгоритм шейкер-сортировки выгодно использовать в тех случаях, когда известно, что элементы уже почти упорядочены – редкий случай на практике.
Можно показать, что среднее расстояние, на которое должен переместиться каждый из n элементов во время сортировки, – это n/3 мест. Это число дает ключ к поиску усовершенствованных, т. е. более эффективных методов сортировки. Все простые методы в принципе перемещают каждый элемент на одну позицию на каждом элементарном шаге. Поэтому они требуют порядка n2 таких шагов. Любое улучшение должно основываться на принципе пересылки элементов за один цикл на большее расстояние.
Сортировка Шелла
Некоторое усовершенствование сортировки простыми вставками было предложено Д.Л. Шеллом в 1959 г. Этот метод продемонстрируем на примере из восьми элементов (рис. 4.1).
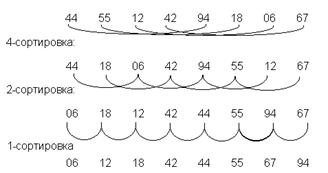
Рис. 4.1. Сортировка Шелла
На первом проходе отдельно группируются и сортируются все элементы, отстоящие друг от друга на четыре позиции. Этот процесс называется 4-сортировкой. В нашем примере из восьми элементов каждая группа содержит ровно два элемента. После этого элементы вновь объединяются в группы с элементами, отстоящими друг от друга на две позиции, и сортируются заново. Этот процесс называется 2-сортировкой. Наконец, на третьем проходе все элементы сортируются обычной сортировкой или 1-сортировкой.
Сначала может показаться, что необходимость нескольких проходов сортировки, в каждом из которых участвуют все элементы, больше работы потребует, чем сэкономит. Однако на каждом шаге сортировки либо участвует сравнительно мало элементов, либо они уже довольно хорошо упорядочены и требуют относительно мало перестановок.
Очевидно, что этот метод в результате дает упорядоченный массив, и также совершенно ясно, что каждый проход будет использовать результаты предыдущего прохода, поскольку каждая i-сортировка объединяет две группы, рассортированные предыдущей 2i-сортировкой. Также ясно, что приемлема любая последовательность приращений, лишь бы последнее было равно 1, так как в худшем случае вся работа будет выполняться на последнем проходе. Однако менее очевидно, что метод убывающего приращения дает даже лучшие результаты, когда приращения не являются степенями двойки.
Таким образом, программа разрабатывается вне связи с конкретной последовательностью приращений. Все t приращений обозначаются через 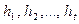 с условиями
с условиями 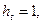
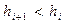 .
.
Каждая h-сортировка программируется как сортировка простыми включениями, при этом, для того чтобы условие окончания поиска места включения было простым, используется барьер.
Ясно, что каждая h-сортировка требует собственного барьера и что программа должна определять его место как можно проще. Поэтому массив a нужно дополнить не одной компонентой а [0], a 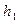 компонентами, так что теперь он описывается как
компонентами, так что теперь он описывается как
а: array [- 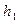 .. n] of item;
.. n] of item;
Вот так будет выглядеть алгоритм сортировки Шелла для t = 4.
procedure shellsort;
const t = 4;
var i,j,k,s: index;
x: item;
m: 1..t;
h: array [1..t] of integer;
begin
h[1] := 9; h[2] := 5; h[3] := 3; h[4] := 1;
for m := 1 to t do begin
k := h[m];
s := – k; {место барьера}
for i := k + 1 to n do begin
x := a[i]; j := i-k;
if s=0 then s := – k;
s := s + 1; a[s] := x;
while x .key < a[j] .key do begin
a[j+k] := a[j]; j := j-k
end ;
a[j+k] := x;
end
end
end;
Анализ сортировки Шелла. При анализе этого алгоритма возникают некоторые очень сложные математические задачи, многие из которых еще не решены. В частности, неизвестно, какая последовательность приращений дает лучшие результаты. Однако выявлен удивительный факт, что они не должны быть кратны друг другу. Это позволяет избежать явления, которое видно в приведенном выше примере, где каждый проход сортировки объединяет две цепочки, которые ранее никак не взаимодействовали. В действительности желательно, чтобы взаимодействие между разными цепочками происходило как можно чаще. Можно сформулировать следующую теорему:
Если k-рассортированная последовательность i-сортируется, то она остается k-рассортированной.
Д. Кнут указывает, что разумным выбором может быть такая последовательность приращений (записанная в обратном порядке):
1, 4, 13, 40, 121, ...,
где 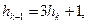
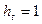 и
и 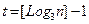 .
.
Он рекомендует также последовательность
1, 3, 7, 15, 31, ...,
где 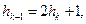
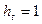 и
и 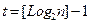 .
.
Дальнейший анализ показывает, что в последнем случае затраты, которые требуются для сортировки n элементов с помощью алгоритма сортировки Шелла, пропорциональны n6/5. Это значительное улучшение по сравнению с n2.
