Рассмотрим некоторые особенности алгоритма Гаусса

Первая особенность состоит в том, что иногда в уравнениях системы отсутствуют некоторые переменные, например:

Как правильно записать расширенную матрицу системы? Об этом моменте мы уже рассказывали на уроке Правило Крамера. Матричный метод. В расширенной матрице системы на месте отсутствующих переменных ставим нули:

Кстати, это довольно легкий пример, поскольку в первом столбце уже есть один ноль, и предстоит выполнить меньше элементарных преобразований.

Вторая особенность состоит вот в чём. Во всех рассмотренных примерах на «ступеньки» мы помещали либо –1, либо +1. Могут ли там быть другие числа? В ряде случаев могут. Рассмотрим систему:

.

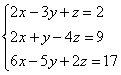Здесь на левой верхней «ступеньке» у нас двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка – и другая двойка и шестерка.

И двойка слева вверху нас устроит! На первом шаге нужно выполнить следующие преобразования: ко второй строке прибавить первую строку, умноженную на (–1); к третьей строке прибавить первую строку, умноженную на (–3). Таким образом, мы получим нужные нули в первом столбце. Или еще такой условный пример:

.

Здесь тройка на второй «ступеньке» тоже нас устраивает, поскольку 12 (место, где нам нужно получить ноль) делится на 3 без остатка. Необходимо провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на (–4), в результате чего и будет получен нужный нам ноль.

Метод Гаусса универсален, но есть одно своеобразие. Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жёсткий алгоритм. Но вот, чтобы уверенно себя чувствовать в методе Гаусса, следует «набить руку», и прорешать хотя бы 5-10 десять систем. Поэтому поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного или трагического. Для желающих более сложный пример для самостоятельного решения:

Пример 5

Решить методом Гаусса систему 4-х линейных уравнений с четырьмя неизвестными.

Такое задание на практике встречается не так уж и редко. Думаю, даже чайнику, который обстоятельно изучил эту страницу, интуитивно понятен алгоритм решения такой системы. Принципиально всё так же – просто действий больше.

Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением. Там же можно закрепить рассмотренный алгоритм метода Гаусса.

Решения и ответы:

Пример 2: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.

Выполненные элементарные преобразования:

(1). Ко второй строке прибавили первую строку, умноженную на (–2). К третьей строке прибавили первую строку, умноженную на (–1). Внимание! Здесь может возникнуть соблазн из третьей строки вычесть первую, крайне не рекомендую вычитать – сильно повышается риск ошибки. Только складываем!

(2). У второй строки сменили знак, умножили на (–1). Вторую и третью строки поменяли местами. Обратите внимание, что на «ступеньках» нас устраивает не только единица, но еще и (–1), что даже удобнее.

(3). К третьей строке прибавили вторую строку, умноженную на 5.

(4). У второй строки сменили знак, умножили на (–1). Третью строку разделили на 14.

(5). Обратный ход:

Ответ: .

Пример 4:

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Выполненные преобразования:

(1). К первой строке прибавили вторую. Таким образом, организована нужная единица на левой верхней «ступеньке».

(2). Ко второй строке прибавили первую строку, умноженную на 7. К третьей строке прибавили первую строку, умноженную на 6. Со второй «ступенькой» всё хуже, «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо (–1). Преобразования (3) и (4) будут направлены на получение нужной единицы

(3). К третьей строке прибавили вторую, умноженную на (–1).

(4). Ко второй строке прибавили третью, умноженную на (–3). Нужная вещь на второй ступеньке получена.

(5). К третьей строке прибавили вторую, умноженную на 6.

(6). Вторую строку умножили на (–1), третью строку разделили на (-83).

(7). Обратный ход: ,

,

.

Ответ: .

Пример 5:

Запишем матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Выполненные преобразования:

(1). Первую и вторую строки поменяли местами.

(2). Ко второй строке прибавили первую строку, умноженную на (–2). К третьей строке прибавили первую строку, умноженную на (–2). К четвертой строке прибавили первую строку, умноженную на (–3).

(3). К третьей строке прибавили вторую, умноженную на 4. К четвертой строке прибавили вторую, умноженную на –1.

(4). У второй строки сменили знак. Четвертую строку разделили на 3 и поместили вместо третьей строки.

(5). К четвертой строке прибавили третью строку, умноженную на (–5).

(6). Обратный ход:

Ответ: