Етодические указания к выполнению задания 1.
адание 1.
Для своего варианта рассчитать:
1. Эквивалентное сопротивление цепи.
2. Ток в каждом резисторе.
3. Проверить выполнение первого закона Кирхгофа во всех узлах схемы и второго Закона Кирхгофа для одного из контуров.
4. Определить мощности, рассеиваемые на резисторах схемы.
5. Проверить выполнение баланса мощностей.
Исходные данные для расчета приведены в табл. 1.1 и табл. 1.2.
Таблица 1.1
| № варианта (две последние цифры номера зачетки) | № рисунка | R1, кОм | R2, кОм | R3, кОм | R4, кОм | R5, кОм | R6, кОм | R7, кОм | R8, кОм |
| 01 – 33 | 1.01 - 1.33 | 1,2 | 2,0 | 0,3 | 1,5 | 1,8 | 1,2 | 3,0 | 2,2 |
| 34 – 66 | 1.01 - 1.33 | 0,3 | 1,0 | 1,5 | 2,7 | 0,2 | 1,3 | 0,3 | 1,6 |
| 67 – 99 | 1.01 - 1.33 | 1,8 | 1,1 | 2,0 | 0,3 | 1,5 | 1,2 | 0,2 | 1,3 |
Например, последние две цифры шифра 37. Следовательно, в соответствии с табл. 1.1 для анализа выбирается схема, приведенная на рис. 1.04, а значения резисторов выбираются из строки 2.
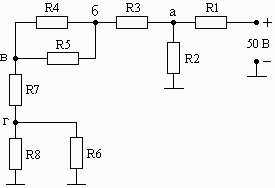
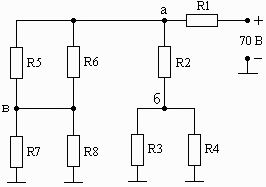
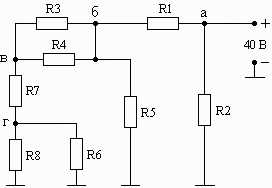
Схема 1.01 Схема 1.02 Схема 1.03
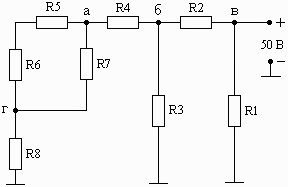
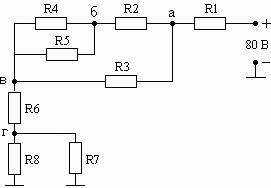
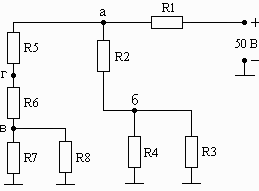
Схема 1.04 Схема 1.05 Схема 1.06
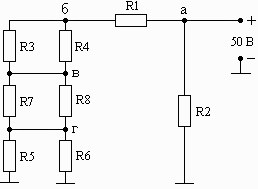
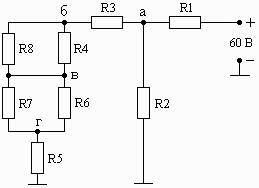
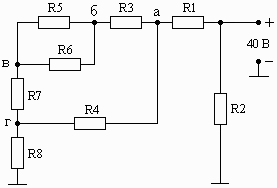
Схема 1.07 Схема 1.08 Схема 1.09
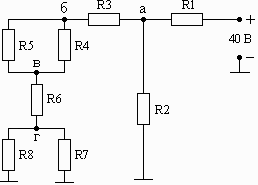
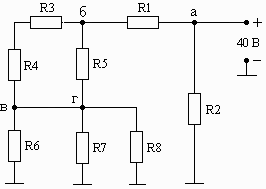
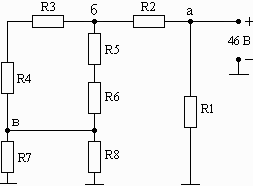
Схема 1.10 Схема 1.11 Схема 1.12
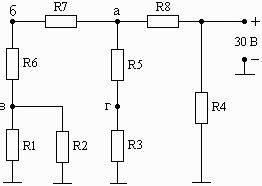
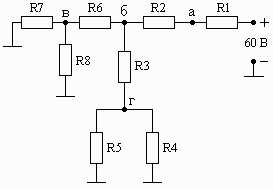
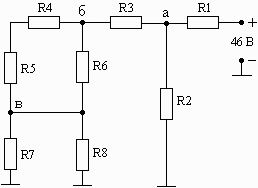
Схема 1.13 Схема 1.14 Схема 1.15
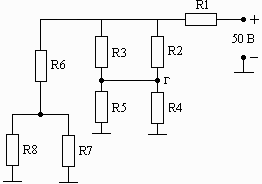
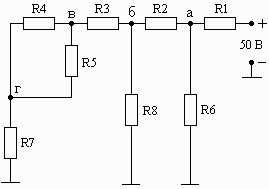
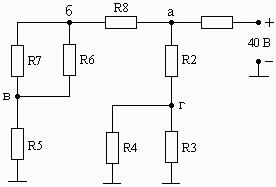
Схема 1.16 Схема 1.17 Схема 1.18
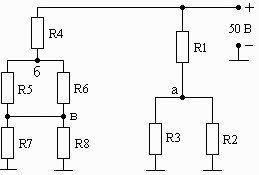
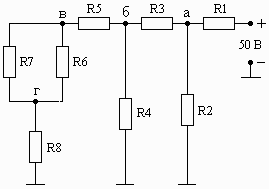
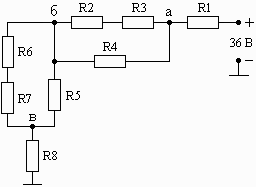
Схема 1.19 Схема 1.20 Схема 1.21
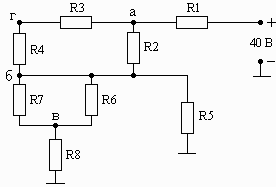
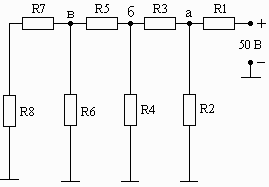
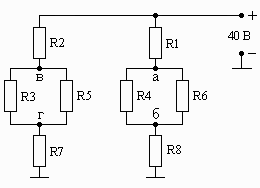
Схема 1.22 Схема 1.23 Схема 1.24

Схема 1.25 Схема1.26 Схема 1.27

Схема 1.28 Схема 1.29 Схема 1.30

Схема 1.31 Схема 1.32 Схема 1.33
Рис. 1. Схемы электрических цепей для задачи 1
адание 2
Рассчитайте токи во всех ветвях цепи по методу контурных токов (МКТ) или методу узловых напряжений (МУН), метод выбирается на усмотрение студента. Произведите проверку баланса мощностей. Схему цепи и сопротивления резисторов выбрать в соответствии с своим вариантом mn.
Задание 3.
Для цепи переменного тока:
1. Рассчитать полное сопротивление цепи при гармоническом воздействии.
2.Найти ток, протекающий через цепь, если на вход подано напряжение, изменяющееся по гармоническому закону.
3. Построить векторную диаграмму тока и напряжения.
Схему цепи и номиналы элементов выбрать в соответствии с вариантом mn - :
для номера зачетки с последними цифрами 01-30 брать соответствующий номер варианта;для номера зачетки 31-60 брать номер варианта mn-30 и т.п.
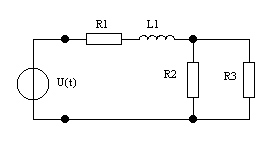
ариант № 1.
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 104 рад/с,
), U = 1 В, ω0 = 104 рад/с,
φ  = π/4. R1 = R2 = R3 = 100 Ом, C1 = 2 мкФ.
= π/4. R1 = R2 = R3 = 100 Ом, C1 = 2 мкФ.
 Вариант № 2.
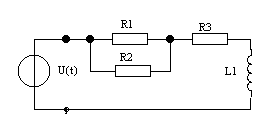
Вариант № 2.
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0= 104 рад/с,
), U = 1 В, ω0= 104 рад/с,
φ0 = π/3. R1 = R2 = R3 = 100 Ом, L1 = 5 мГн.
.
ариант № 3.
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 104 рад/с,
), U = 1 В, ω0 = 104 рад/с,
φ0 = π/4, R1 = R2 = R3 = 10 Ом, L1 = 1 мГн.
ариант № 4.
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 104 рад/с,
), U = 1 В, ω0 = 104 рад/с,
φ0 = π/3, R1 = R2 = R3 =10 Ом, C1 = 10 мкФ.
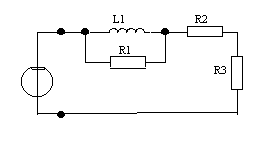
ариант № 5.
Дано: u(t)=Ucos(ωt + φ  ), U=1 В, ω0 =104 рад/с,
), U=1 В, ω0 =104 рад/с,
φ0 = π/4. R1 = 100 Ом, R2 = R3 = 10 Ом, C1 = 2 мкФ.
| u(t) |
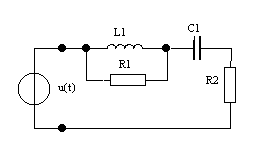
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 104 рад/с,
), U = 1 В, ω0 = 104 рад/с,
φ0 = π/3. R1 = 100 Ом, R2 = R3 = 10 Ом, L1 = 10 мГн.
 Вариант № 7.
Вариант № 7.
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 10 рад/с,
), U = 1 В, ω0 = 10 рад/с,
φ0 = π/4. R1 = 100 Ом, R2 = 10 Ом, C1 = 10 мкФ.,
L1 = 10 мкФ.
ариант № 8.
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 10 рад/с, φ0 = π/3.
), U = 1 В, ω0 = 10 рад/с, φ0 = π/3.
R2 = 10 Ом, R1 = 100 Ом, L1 = 10 мГн., L2 = 5 мГн.
| u(t) |
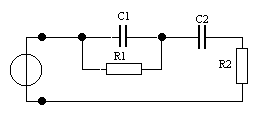
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 10 рад/с, φ0 = π/4.
), U = 1 В, ω0 = 10 рад/с, φ0 = π/4.
R1 = 100 Ом, R2 = 10 Ом, C2 = 2 мкФ., C1 = 1 мкФ.
.
| u(t) |
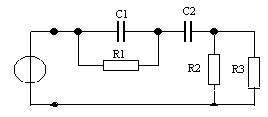
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 10 рад/с,
), U = 1 В, ω0 = 10 рад/с,
φ0 = π/4. R1 = R2 = R3 = 100 Ом, C1 = C2 = 1 мкФ.
| u(t) |
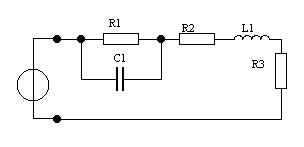
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 10 рад/с,
), U = 1 В, ω0 = 10 рад/с,
φ0 = π/4. R1 = 1 кОм, R2 = R3 = 10 Ом, C1 = 0.01 мкФ,
L1 = 0.5 мГн.
| u(t) |
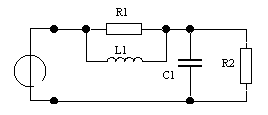
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 104 рад/с,
), U = 1 В, ω0 = 104 рад/с,
φ0 = π/4. R1 = R2 = 10 кОм, C1 = 0.01 мкФ., L1 = 1 мГн.
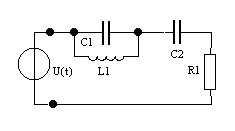 Вариант № 13.
Вариант № 13.
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 104 рад/с, φ0 = π/3.
), U = 1 В, ω0 = 104 рад/с, φ0 = π/3.
R1 = 50 Ом, C1 = 0.01 мкФ., C2 = 0.02 мкФ., L1 = 10 мГн.
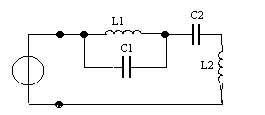
| u(t) |
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 10 рад/с,
), U = 1 В, ω0 = 10 рад/с,
φ0 = π/4. C1 = 1 мкФ., C2 = 5 мкФ., L2 = 2 мГн., L1 = 10 мГн.
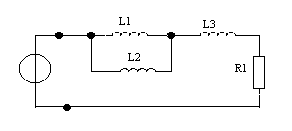
| u(t) |
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 10 рад/с, φ0 = π/4. R1 = 10 Ом, L1 = 4 мГн., L2 = 2 мГн, L3 = 1 мГн.
), U = 1 В, ω0 = 10 рад/с, φ0 = π/4. R1 = 10 Ом, L1 = 4 мГн., L2 = 2 мГн, L3 = 1 мГн.
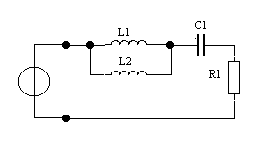
| u(t) |
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 105 рад/с,
), U = 1 В, ω0 = 105 рад/с,
φ0 = π/2. R1 = 10 Ом, C1 = 0.01 мкФ., L1 = 0.05 мГн,
L2 = 0.1 мГн.
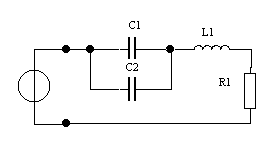
| u(t) |
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 104 рад/с, φ0 = π/4.
), U = 1 В, ω0 = 104 рад/с, φ0 = π/4.
R1 = 10 Ом, C2 = 0.5 мкФ.,C1 = 0.2 мкФ., L1 = 0.01 мГн.
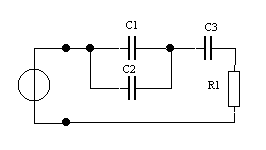
| u(t) |
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 10 рад/с, φ0 = π/4. R1 = 10 Ом, C1 = C2 = 1 мкФ., C3 = 5 мкФ.
), U = 1 В, ω0 = 10 рад/с, φ0 = π/4. R1 = 10 Ом, C1 = C2 = 1 мкФ., C3 = 5 мкФ.
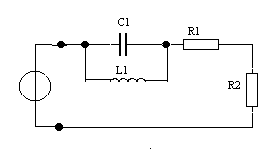
| u(t) |
Дано: u(t) = Ucos(ωt + φ  ),U = 1 В, ω0 = 104 рад/с, φ0 = π/3.
),U = 1 В, ω0 = 104 рад/с, φ0 = π/3.
R1 = 10 Ом, R2 = 20 Ом, C1 = 0.01 мкФ.,L1 = 0.1 мГн.
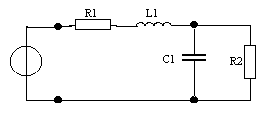
| u(t) |
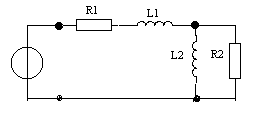
Дано: u(t) = Ucos(ωt + φ  ),U = 1 В, ω0 = 10 рад/с, φ0 = π/4. R1 = 10 Ом, R2 = 10 кОм, L1 = 0.5 мГн.,C1 = 0.01 мкФ.
),U = 1 В, ω0 = 10 рад/с, φ0 = π/4. R1 = 10 Ом, R2 = 10 кОм, L1 = 0.5 мГн.,C1 = 0.01 мкФ.
| u(t) |
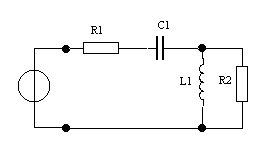
Дано: u(t)=Ucos(ωt + φ  ), U=1 В, ω0 =105 рад/с, φ0 = π/2. R1=R2=100 Ом, L2=20 мГн.,L1=5 мГн
), U=1 В, ω0 =105 рад/с, φ0 = π/2. R1=R2=100 Ом, L2=20 мГн.,L1=5 мГн
| u(t) |
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 10 рад/с, φ0 = π/3.
), U = 1 В, ω0 = 10 рад/с, φ0 = π/3.
R1 = 10 Ом, R2 = 10 кОм, C1 = 0.2 мкФ., L1 = 0.02 мГн.
ариант № 23.
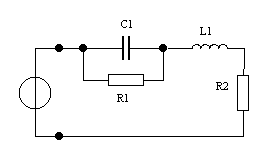
Дано: u(t)=Ucos(ωt + φ  ), U = 1 В, ω0 = 10 рад/с, φ0 = π/4.
), U = 1 В, ω0 = 10 рад/с, φ0 = π/4.
R1 = R2 = 100 Ом, C1 = 5 мкФ., C2 = 1 мкФ.
| u(t) |
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 10 рад/с, φ0 = π/3. R1 = 10 кОм, R2 = 10 Ом, C1 = 0.01 мкФ., L1 = 0.2 мГн.
), U = 1 В, ω0 = 10 рад/с, φ0 = π/3. R1 = 10 кОм, R2 = 10 Ом, C1 = 0.01 мкФ., L1 = 0.2 мГн.
ариант № 25.
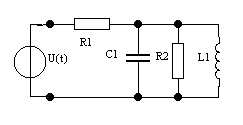
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 10 рад/с,
), U = 1 В, ω0 = 10 рад/с,
φ0 = π/4. R1 = R2 =10 кОм, R3 = 100 Ом, C1 = 0.02 мкФ, L1 = 0.5 мГн.
 Вариант № 26.
Вариант № 26.
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 10 рад/с, φ0 = π/4.
), U = 1 В, ω0 = 10 рад/с, φ0 = π/4.
R1 = 10 Ом, R2 = 100 кОм, С1 = 1000 пФ, L1 = 0.1 мГн.
ариант № 27.
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 10 рад/с, φ0 = π/4.
), U = 1 В, ω0 = 10 рад/с, φ0 = π/4.
R1 = 10 Ом, R2 = 20 Ом, С1 = 1000 пФ, L1 = 0.1 мГн.
ариант № 28.
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 10 рад/с, φ0 = π/4.
), U = 1 В, ω0 = 10 рад/с, φ0 = π/4.
R1 = 10 Ом, R2 = 20 Ом, С1 = 1000 пФ, L1 = 0.1 мГн.
ариант № 29.
Дано: u(t)=Ucos(ωt+φ  ), U=1 В, ω0 =10 рад/с, φ0 = π/4.
), U=1 В, ω0 =10 рад/с, φ0 = π/4.
R1=10 Ом, R2=10 кОм, С1=500 пФ, L1=0.01 мГн.
ариант № 30.
Дано: u(t) = Ucos(ωt + φ  ), U = 1 В, ω0 = 104 рад/с, φ0 = π/4.
), U = 1 В, ω0 = 104 рад/с, φ0 = π/4.
R1=10 Ом, R2=20 Ом, С1=1000 пФ, L1=0.1 мГн
Задание 4
Найти полную, активную и реактивную мощности, потребляемые нагрузкой, для цепи рассчитанной в задании 3,
Методические указания к выполнению контрольной работы по разделу Основы электротехнтки
етодические указания к выполнению задания 1.
Решение этой задачи требует знания закона Ома для всей цепи и ее участков, первого закона Кирхгофа и методики определения эквивалентного сопротивления цепи при смешанном соединении резисторов.
Электрические цепи подразделяются на простые и сложные. Цепь, в которой имеется единственный путь для тока, называется простой цепью. Расчет тока в такой цепи (рис. 2.4) осуществляется по закону Ома
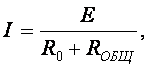
где ROБЩ – общее сопротивление потребителей (нагрузки); U – напряжение на зажимах источника ЭДС.
При последовательном соединении приемников
ROБЩ = R1 + R2.
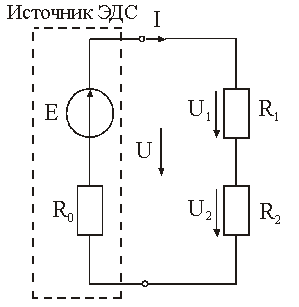 Рис. 2.4. – Простая электрическая цепь с последовательным соединением элементов Рис. 2.4. – Простая электрическая цепь с последовательным соединением элементов | Рис. 2.5. – Сложная электрическая 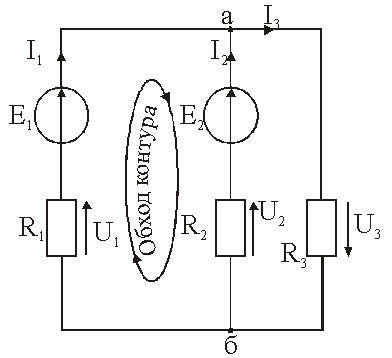 цепь цепь |
Цепь, в которой имеется три (или более) пути для токов, называется сложной цепью (рис. 2.5).
Сложная цепь состоит из узлов и ветвей. Ветвь – это участок электрической цепи, обтекаемый одним током. Все элементы ветви (источники, приёмники) соединены последовательно. В электрической цепи количество токов равно количеству ветвей.
Узел – это место соединения трех или более ветвей (узлы "а" и "б" на рис. 2.5).
Контур-состоит из ветвей, которые образуют замкнутый путь для протекания электрического тока.
2.2. Законы Кирхгофа
Согласно первого закона Кирхгофа алгебраическая сумма токов в любом узле электрической цепи равна нулю
∑I = 0.
Поскольку речь идет об алгебраической сумме ∑I, необходимо учитывать знаки слагаемых токов. Входящие в узел токи принято считать положительными, выходящие – отрицательными. Для узла "а" (рис. 2.5) имеем
I1 + I2 - I3 = 0.
Согласно второго закона Кирхгофа алгебраическая сумма ЭДС в любом контуре цепи равна алгебраической сумме падений напряжений на элементах контура
∑E = ∑R·I.
Для составления уравнения по второму закону Кирхгофа произвольно выбирают направление обхода контура. Принято ЭДС, токи и напряжения считать положительными, если они совпадают по направлению с направлением обхода контура, а если не совпадают – отрицательными. При обходе контура E1, E2, R2, R1 электрической цепи (рис. 2.5) по часовой стрелке имеем
E1 - E2 = R1·I1 - R2 I2.
