Задания для лабораторной работы

Занятие 1. Передача переменных и выражений при вызове функций (передача данных по значению при вызове функции).

Пример 1 Предположим, необходимо вычислить

z=(ax+b)(cx+d)²+(acx+bd)³((a+c)x+b+d)⁴;

Здесь z равно сумме произведений полиномов, которые отличаются коэффициентами при х, свободными членами и степенями, в которые эти полиномы нужно возвести.

В принципе можно написать одно выражение на СИ для вычисления z, но оно будет громоздким. В то же время можно создать отдельную функцию, в которую передавать все исходные данные для вычисления полинома и возведения его в степень, и с помощью этой функции вычислить z .

При написании программы следует вспомнить, что для локальных переменных каждой из функций выделяется отдельная память. Поэтому допускается совпадение символических имен переменных в разных функциях. Следовательно, допускается, чтобы символические имена формальных параметров в функции совпадали с именами фактических параметров при вызове этой функции.

#include<stdio.h>

#include<math.h>

float f(float a, float x, float b, int stepen);

void main()

{

float z, a, x, b, c, d ;

puts(“Введите a,x,b,c,d ”);

scanf(“%f%f%f%f%f”,&a,&x,&b,&c,&d);

z=f(a,x,b,1)*f(c,x,d,2)+f(a*c,x,b*d,3)*f(a+c,x,b+d,4);

printf(“z=%f\n”,z);

}

float f(float a, float x, float b, int stepen)

{

float v;

v=pow(a*x+b,stepen);

return v;

}

Эту функцию можно было написать проще:

float f(float a, float x, float b, int stepen)

{

return pow(a*x+b, stepen);

}

При первом вызове f(a,x,b,1) фактические параметры имеют такие же имена, как и формальные. Однако еще раз следует подчеркнуть, что это разные переменные и для каждой, выделена своя память. Копии значений фактических переменных a,x,b присваиваются формальным параметрам a,x,b, а 1 присваивается формальному параметру stepen.

Возвращенный результат, в свою очередь, умножается на f(c,x,d,2). Теперь уже копии фактических параметров c,x,d присваиваются соответственно формальным параметрам a,x,b, а константа 2 присваивается формальному параметру stepen.

При вызовах f(a*c,x,b*d) и f(a+c,x,b+d) сначала вычисляются выражения, и копии результатов вычислений присваиваются формальным параметрам. Так, для f(a*c,x,b*d,3) результат умножения a*c будет присвоен формальному параметру а, а b*d – формальному параметру b.

При вызове f(a+c,x,b+d,4) результаты сложения a+c и b+d будут присвоены соответственно формальным параметрам а и b.

Так передаются при вызове функции данные по значению.

Задания для лабораторной работы

1. Заданы массивы X[N],Y[N] (N<20). Сформировать массив Z[N], каждый элемент которого вычисляется по формуле

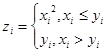
Вычисление Z_i оформить в виде функции

2. Заданы массивы X[N],Y[N] (N<20). Сформировать массив Z[N], каждый элемент которого вычисляется по формуле

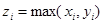
Вычисление Z_i оформить в виде функции

3. Заданы массивы X[N],Y[N] (N<20). Сформировать массив Z[N], каждый элемент которого вычисляется по формуле

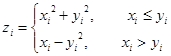
Вычисление Z_i оформить в виде функции

4 Заданы массивы P[N],Q[N] (N<20). Сформировать массив Z[N], каждый элемент которого равен большему корню уравнения Z²+P_i Z+Q_i=0, если дискриминант >=0, и рамен 10³⁸, если дискриминант <0.

5 Заданы массивы P[N],Q[N] (N<20). Сформировать массив Z[N], каждый элемент которого равен меньшему корню уравнения Z²+P_i Z+Q_i=0, если дискриминант >=0, и рамен -10³⁸, если дискриминант <0.

6. Вычислить 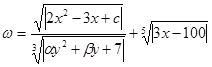. Вычисления осуществить с использованием функции.

7. Вычислить 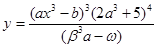. Вычисления осуществить с использованием функции.

8. Вычислить значения функции Х, если а изменяется от а_нач до а_кон с шагом Δа. Вычисления осуществить с использованием функции.

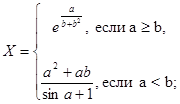
9. Вычислить значения функции Х, если а изменяется от а_нач до а_кон с шагом Δа. Вычисления осуществить с использованием функции.

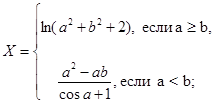
10 . Вычислить значения функции у, если х изменяется от х_нач до х_кон с шагом Δх. Вычисления осуществить с использованием функции. Значение функции y=f(x) вычисляется в зависимости от номера точки i

i делится на 3 без остатка у=sin x ;

остаток от деления i на 3=1 y=cos x;

остаток от деления i на 3=2 y=tg x.