Алгоритм построения дерева
- Символы исходного алфавита образуют список свободных узлов. Каждый узел имеет вес, равный количеству вхождений символа в исходное сообщение.
- В списке выбираются два свободных узла с наименьшими весами.
- Создается их узел «родитель» с весом, равным сумме их весов, он соединяется с «детьми» дугами.
- Одной дуге, выходящей из «родителя» ставится в соответствии «1» бит, другой – «0».
- «Родитель» добавляется в список свободных узлов, а двое «детей» удаляются из списка.
- Шаги 2-6 повторяются до тех пор, пока в списке свободных узлов не останется.
Пример: построить дерево Хаффмана и найти префиксные коды для сообщения: «КОЛ_ОКОЛО_КОЛОКОЛА»
Решение:
· Составим таблицу частот вхождения символов
| О | К | Л | пробел | А |
· Построим дерево Хаффмана
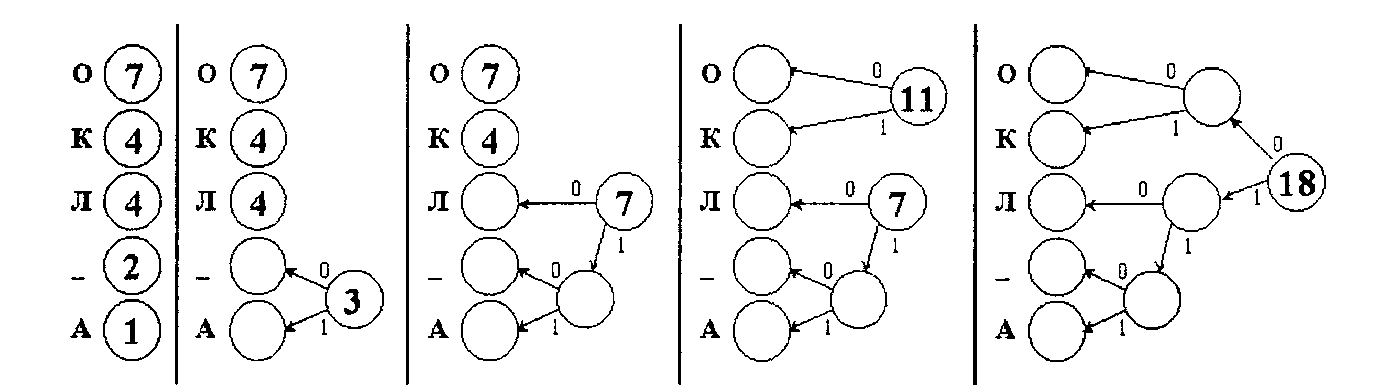
Блочное кодирование по методу Хаффмана формирует коды для буквосочетаний, составленных из m символов исходного алфавита.
Буквосочетания можно рассматривать как новый, расширенный алфавит объемом
K=Nm , где
N – объем исходного алфавита;
M – число символов в буквосочетании.
Блочное кодирование применяется к алфавитам, в которых вероятность появления одной какой-то буквы значительно превышает вероятность появления других букв.
Рассчитаем коэффициент сжатия сообщения.
Пример 3. Вычислили объем сообщения «КОЛ ОКОЛО КОЛОКОЛА» при использовании кодировок ASCII (Vascii =144 бита) и Unicode (Vunicode = 288 бит). Выше построили код Хаффмана для этой же фразы, на основании которого оценили объем сообщения Vхаффмана=39 бит.
В результате мы получаем коэффициент сжатия равный 144/39 = 3,7 для кодировки ASCII и 288/39 =7,4 для кодировки Unicode.
Метод RLE
В основу алгоритмов RLE (Run-Length Encoding – кодирование путем учета числа повторений) положен принцип выявления повторяющихся последовательностей данных и замены их простой структурой: повторяющийся фрагмент и коэффициент повторения.
Рассмотрим идею сжатия методом RLE. Во входной последовательности:
1. все повторяющиеся цепочки байтов заменяются на фрагменты {управляющий байт, повторяющийся байт}, причем управляющий байт в десятичной системе счисления должен иметь значение 128 + число повторений байта. Это означает, что старший бит управляющего байта для цепочки повторяющихся байтов всегда равен 1.
2. все неповторяющиеся цепочки байтов заменяются на фрагменты {управляющий байт, цепочка неповторяющихся байтов}, причем управляющий в десятичной системе счисления должен иметь значение 0+ длина цепочки. Это означат, что старший бит управляющего байта для цепочки неповторяющихся байтов всегда равен 0.
Замечание. В обоих случаях длина обрабатываем фрагмента не может превосходить 127 байт.
Пример 4. Упакуем методом RLE следующую последовательность из 14-ти байтов:
11111111 11111111 11111111 11111111 11111111 11110000 00001111 11000011 10101010 10101010 10101010 10101010 10101010 10101010
В начале последовательности 5 раз повторяется байт 11111111. Чтобы закодировать эти 5-ть байтов, запишем вначале управляющий байт 10000101, а затем сам повторяющийся байт 11111111. Рассмотрим как получился управляющийся байт: к значению 128 мы прибавили число повторений байта 5, получили 13310=100001012.
Далее идут 3 разных байта. Чтобы их закодировать, мы записываем управляющий байт 00000011 (112=310), а затем эти неповторяющиеся байты.
Далее в последовательности 7 раз идет байт 10101010. Чтобы закодировать эти 7 байтов, мы записываем управляющий байт 10000111 (128+7=13510=10001112), а затем повторяющийся байт 10101010.
В результате применения метода RLE мы получаем последовательность из 8-ми байтов: 10000101 11111111 00000011 11110000 00001111 11000011 10000111 10101010.
Таким образом, коэффициент сжатия 14/8=1,75.
Схема распаковки:
1. Если во входной (сжатой) последовательности встречается управляющий байт с единицей в старшем бите, то следующий за ним байт данный надо записать в выходную последовательность столько раз, сколько указано в оставшихся 7-ми битах управляющего байта.
2. Если во входной (сжатой) последовательности управляющий байт с нулем в старшем бите, то в выходную последовательность нужно поместить столько следующих за управляющим байтов входной последовательности, сколько указано в оставшихся 7-ми битах управляющего байта.
Пример 5. Распакуем сжатую последовательность данных методом RLE:
00000010 00001111 11110000 10000110 11000011 00000011 00001111 00111100 01010101.
Первый байт данной последовательности управляющий 000000010, начинается с 0. Следовательно, следующие за ним 102=210 байта помещаются в выходную последовательность.
Замечание. Будем зачеркивать обработанные байты.
00000010 00001111 11110000 10000110 11000011 00000011 00001111 00111100 01010101
Следующий управляющий байт 10000110 начинается с 1. Следовательно, следующий за ним байт нужно поместить в выходную последовательность 1102=610 раз.
00000010 00001111 11110000 10000110 11000011 00000011 00001111 00111100 01010101
Следующий управляющий байт 00000011 начинается с 0. Следовательно, следующие за ним 112=310 байта нужно поместить в выходную последовательность.
Таким образом, все входные данные мы обработали. А распакованная последовательность байтов выглядит следующим образом:
00001111 11110000 11000011 11000011 11000011 11000011 11000011 11000011 00001111 00111100 01010101
Наилучшими объектами для данного алгоритма являются графические данные, в которых встречаются большие одноцветные участки. Различные реализации данного метода используются в графических форматах PCX, BMP и факсимильной передаче информации. Для текстовых данных данный метод неэффективен.
