Ланирование и проведение вычислительного эксперимента

сходные данные

Цель работы: Смоделировать работу ЛВС, состоящей из файлового сервера и пяти рабочих станций. Определить коэффициент загрузки файлового сервера.

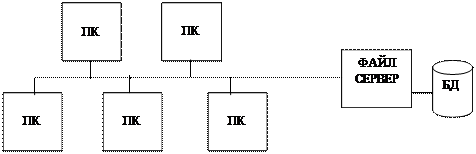
Задание: Смоделировать работу ЛВС магистральной конфигурации, состоящей из файлового сервера и пяти рабочих станций. База данных ведется на ВЗУ файлового сервера. Обмен сообщениями между абонентами сети осуществляется через сервер. Пользователи могут читать данные из базы и проводит их актуализацию. Известны характеристики потоков запросов на обращение к базе данных и на обмен сообщениями 3000 и 4000 запросов в час соответственно, а также среднее время обработки названных запросов в файловом сервере – 3 и 5 секунд соответственно. Определить коэффициент загрузки файлового сервера. Скорость передачи данных по моноканалу в ЛВС – 10 Мбит/с.

азработка имитационной модели

2.1. Структурная схема:

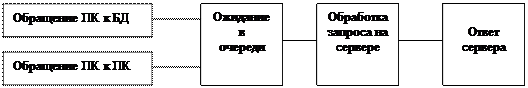2.2. Исходные данные:

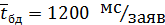- интенсивность потока заявок обращений к БД

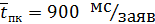- интенсивность потока заявок обращений к ПК

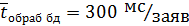- время обработки заявки к БД сервером

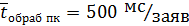- время обработки заявки к ПК сервером

2.3. Определение целей и вида результатов:

Смоделировать обработку сервером необходимого числа заявок. Определить среднюю загрузку системы.

2.4. Ограничения:

a) Оборудование абсолютно надежно.

b) Человеческий фактор исключён.

c) Загрузка системы меньше единицы.

2.5. Допущения:

a) Скорость передачи по каналу в ЛВС не учитывается.

b) 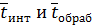распределены по экспоненциальному закону.

c)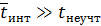

2.6. Математическая модель:

2.7. Моделирующий алгоритм:

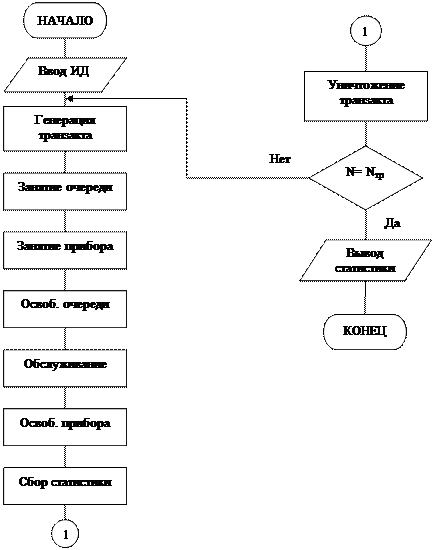
ланирование и проведение вычислительного эксперимента

3.1 Реализация модели:

Для реализации данной модели в качестве вычислительной среды была выбрана ПЭВМ, а в качестве среды моделирования – GPSS.

Листинг программной реализации модели:

SIMULATE

FUN1 FUNCTION RN5,C13

0,0/.1,.105/.2,.223/.3,.357/.4,.511/.5,.593/.6,.916/.7,1.304/.8,1.610

.9,2.303/.97,3.507/.995,5.298/.999,7

GEN1 GENERATE X$NUM1,FN$FUN1 ; K BD

ASSIGN 1,X$NUM3

TRANSFER ,METKA1

GEN2 GENERATE X$NUM2,FN$FUN1 ; K PC

ASSIGN 1,X$NUM4

METKA1 QUEUE OCH

SEIZE CHAN

DEPART OCH

ADVANCE P1,FN$FUN1

RELEASE CHAN

TERMINATE 1

INITIAL X$NUM1,1200

INITIAL X$NUM2,900

INITIAL X$NUM3,300 ;X1

INITIAL X$NUM4,500 ;X2

START 68000

Оценка адекватности модели проводилась посредством проверки разумности результатов моделирования. Модель проверялась по следующим признакам: все ли существенные параметры отражены, правильно ли отражены функциональные связи, правильно ли определены ограничения на параметры, соответствие результатов моделирования здравому смыслу и общепринятым положениям. По результатам был сделан вывод о возможности использования модели.

Пример файла отчета:

START TIME END TIME BLOCKS FACILITIES STORAGES

0.000 35647158.593 11 1 0

NAME VALUE

CHAN 10006.000

FUN1 10000.000

GEN1 1.000

GEN2 4.000

METKA1 6.000

NUM1 10001.000

NUM2 10002.000

NUM3 10003.000

NUM4 10004.000

OCH 10005.000

LABEL LOC BLOCK TYPE ENTRY COUNT CURRENT COUNT RETRY

GEN1 1 GENERATE 29143 0 0

2 ASSIGN 29143 0 0

3 TRANSFER 29143 0 0

GEN2 4 GENERATE 38857 0 0

5 ASSIGN 38857 0 0

METKA1 6 QUEUE 68000 0 0

7 SEIZE 68000 0 0

8 DEPART 68000 0 0

9 ADVANCE 68000 0 0

10 RELEASE 68000 0 0

11 TERMINATE 68000 0 0

FACILITY ENTRIES UTIL. AVE. TIME AVAIL. OWNER PEND INTER RETRY DELAY

CHAN 68000 0.809 424.323 1 0 0 0 0 0

QUEUE MAX CONT. ENTRY ENTRY(0) AVE.CONT. AVE.TIME AVE.(-0) RETRY

OCH 42 0 68000 12709 3.878 2032.723 2499.958 0

SAVEVALUE RETRY VALUE

NUM1 0 1200.000

NUM2 0 900.000

NUM3 0 300.000

NUM4 0 500.000

FEC XN PRI BDT ASSEM CURRENT NEXT PARAMETER VALUE

68002 0 35647385.649 68002 0 4

68001 0 35654383.532 68001 0 1

3.2 Планирование:

При числе факторов 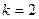и уровнях 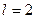общее число точек факторного пространства 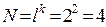. Определим множество управляемых переменных Х={X₁, X₂}, где X₁ - время обработки заявки к БД сервером, X₂ - время обработки заявки к ПК сервером.

Факторы	Уровни факторов
-1	+1
X1
­X­2

Расчёт требуемого числа прогонов осуществим по следующей формуле:

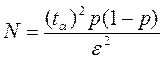
t_α = 2.71 — параметр распределения Стьюдента, определяемый по таблице для доверительной вероятности равной 0.95

p = 0.5 – вероятность наступления события, принят наихудший вариант.

Выберем требуемую точность моделирования 1%

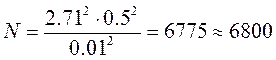
Матрица планирования:

Номер опыта	X0	X1	X2	X1X2	yi
	+1	-1	-1	+1	y1
	+1	+1	-1	-1	y2
	+1	-1	+1	-1	y3
	+1	+1	+1	+1	y4

Число экспериментов в данной работе q=5.

3.3 Проведение испытаний в каждой точке факторного пространства:

Факторы	1-е испытание	2-е испытание	3-е испытание	4-е испытание	5-е испытание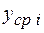
Число точек факторного постранства	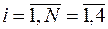X1	X2
	-1	-1	0,61	0,612	0,611	0,608	0,61	0,6102
	+1	-1	0,697	0,694	0,697	0,694	0,699	0,6962
	-1	+1	0,719	0,722	0,724	0,723	0,721	0,7218
	+1	+1	0,804	0,806	0,808	0,8	0,809	0,8054

3.4 Вычисление математического ожидания и дисперсии:

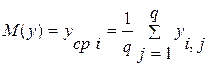- математическое ожидание величины.

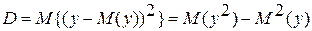- дисперсия случайной величины, где .

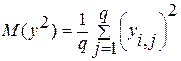Данные промежуточных вычислений и рассчитанные значения дисперсий занесены в таблицу:

	M( 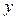)	D
	0,6102	1,76E-06
	0,6962	3,76E-06
	0,7218	2,96E-06
	0,8054	1,024E-05

Пример расчёта:

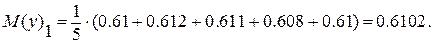
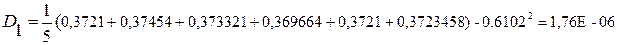
3.5 Проверка однородности дисперсий:

Выдвигаются гипотезы:

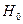- дисперсия однородна (во всех экспериментах дисперсия равна)

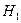- дисперсия неоднородна (во всех экспериментах дисперсия неравна)

Вычисляем наблюдаемое значение(значение статистического критерия по данной выборке):

;

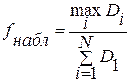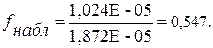
Затем сравниваем полученное значение с ,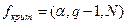

где q – число испытаний;

N – число точек факторного пространства;

α=0,01 - вероятность ошибки I рода.

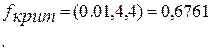
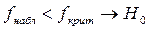- дисперсия однородна.