Энергетические соотношения в

ЭЛЕКТРОМАГНИТНОЙ ВОЛНЕ

В предыдущих параграфах мы выяснили, что переменное электромагнитное поле всегда находится в движении в виде электромагнитной волны (электромагнитного излучения). Электромагнитная волна как материальный объект обладает энергией и переносит энергию в среде своего распространения.

3.7.1. Поток плотности электромагнитной энергии, вектор

Пойнтинга

1.Плотность энергии. Энергия электромагнитного поля локализована в пространстве. Плотность энергии определяет энергию в единице объема:

w = ,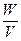

которая складывается из плотности энергии электрического и магнитного полей: w = w_э + w_м = 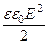+ 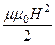, (86)

где E(x, y, z) и H(x, y, z) – мгновенные значения соответственно напряженности электрического и магнитного полей в фиксированный момент времени t. Подчеркнем, формула (86) описывает плотность энергии электромагнитного поля в изотропной среде в отсутствии ферромагнетиков и сегнетоэлектриков.

Попутно заметим, в вакууме w_э = w_м. Действительно, соотношение (46) 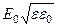= 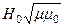(§ 3.5.2,) для амплитудных значений E₀ и H₀в идеальном диэлектрике верно и для других мгновенных значений E и H. Например, мгновенные значения E(x, y, z) и H(x, y, z) в вакууме связаны соотношением 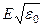= 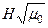(вакууме e = 1 и m = 1). Из этого имеем:

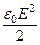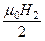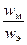= или =1.

Для сравнения вспомним, в проводящей среде 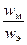» 3×10⁷ (оценка приведена в конце § 3.6.2), что обусловлено незначительным волновым сопротивлением Z₀ проводящей среды.Вследствие поглощения энергии в проводящей среде имеется также сдвиг между фазами колебаний E и H (угол сдвига определяется выражением j = arctg ).

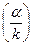Энергия электромагнитного поля в выделенном объеме V определяется интегралом по этому объему:

W = 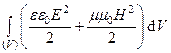. (87)

Электромагнитная волна находится в движении, описываемая волновыми уравнениями (40) и (41). Решением уравнений является монохроматическая волна с частотой w, распространяющаяся в вакууме со скоростью

c = 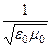» 3×10⁸ .

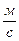Разумеется, реальная электромагнитная волна не является монохроматической, т.к. она ограничена как по протяженности пространстве, так и по длительности во времени. Реальную волну можно рассматривать как совокупность монохроматических волн, частоты которых находятся в некотором диапазоне частот 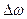. Совокупность волн, образующих реальную электромагнитную волну, называется группой волн или волновым пакетом. В вакууме дисперсия (зависимость фазовой скорости волны от частоты) отсутствует, и все монохроматические составляющие реальной волны распространяются с одной и той же скоростью c » 3×10⁸ м/с. Профиль волнового пакета при распространении волны в вакууме не изменяется. Мгновенное значение напряженности электрического поля E и напряженности магнитного поля H волнового пакета в данной точке пространства определяется векторной суммой векторов E_i и H_i всех монохроматических составляющих волнового пакета.

2.Плотность потока энергии; вектор Пойнтинга. Выражение для плотности энергии волнового пакета в вакууме можно, с учетом соотношения 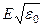= 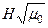, представить в виде:

w = + = ( ) + ( ) =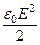

= ( ) + ( ) = .

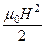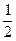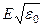
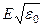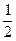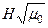
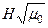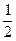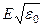
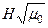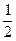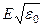
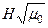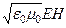Итак, имеем: w = 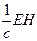. (88)

Произведение плотности энергии электромагнитного поля w на скорость распространения этого поля c есть модуль плотности потока электромагнитной энергии:

П = wс = EH.

Такое же выражение для модуля плотности потока энергии получается и в диэлектрике: П = wv = EH, (89)

где v = 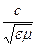- скорость электромагнитной волны в диэлектрике.

Из самого понятия плотности потока энергии следует, что это векторная величина: П = wv. В электромагнитном поле вектор Побразует с векторами E и H правовинтовую систему, и равен векторному произведению E и H:

П = [E, H]. (90)

Вектор П называется вектором Пойнтинга и направлен в сторону распространения электромагнитной энергии.

Определим смысл модуля вектора Пойтинга. Допустим, за время t волна прошла перпендикулярно поверхности S расстояние l. При этом передний фронт волны «заметает» объем V = Sl. Имеем:

П = wv = = .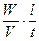

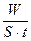Итак, модуль вектора Пойнтинга равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.

Единицу модуля вектора Пойнтинга можно получить из понятия плотности потока энергии П = wv: 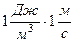= 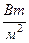. Из определения вектора Пойнтинга П = [E, H] получим, разумеется, тот же результат: = .

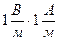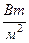Поток электромагнитной энергии Ф, проходящий через произвольную поверхность S за единицу времени, определится интегралом вектора П по этой поверхности:

Ф = 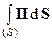или Ф = 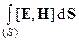. (91)

Поток энергии Ф измеряется в ваттах: 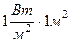= Вт.

Рассмотрим замкнутую поверхность S, охватывающий объем V. Допустим, в этом объеме содержатся электромагнитное поле. Энергия электромагнитного поля W в объеме V с течением времени будет изменяться. Из самых общих соображений можно выделить две причины этого изменения:

1) если в выделенном объеме содержатся объекты, проводящие электрический токи, то электромагнитное поле будет возбуждать ток в проводящих объектах, что приводит к выделению джоулева тепла Q. Вследствие этой причины энергия электромагнитного поля поглощается в самом объеме V (тем самым убывает) и переходит во внутреннюю энергию проводящих объектов;

2) через замкнутую поверхность S, охватывающий объем V, может существовать поток электромагнитной энергии Ф = 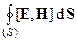. Эта причина приводит или к убыли электромагнитного поля (при потоке из объема V), или к возрастанию энергии электромагнитного поля в выделенном объеме V (при потоке в объем V).

Таким образом, энергетический баланс в объеме V можно выразить уравнением: 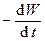= 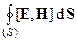+ Q,(92)

где левая часть ( 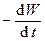) – это скорость убыли электромагнитной энергии в объеме (скорость изменения энергии, взятая с обратным знаком). Уравнение (92) выражает закон сохранения энергии в электромагнитном поле.

Закон сохранения (92) носит название теоремы Умова-Пойнтинга. Покажем, что (92) следует из уравнений Максвелла, тем самым уясним, что уравнения Максвелла опосредованно согласуются с законом сохранения энергии.

3.7.2. Теорема Умова-Пойнтинга

Энергия электромагнитного поля в объеме V складывается из энергии электрического и магнитного полей:

W = .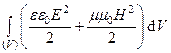

Изменение энергии электромагнитного поля выразится через изменение напряженности электрического поля 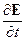и изменение магнитного поля 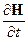. Запишем соответствующие динамические уравнения Максвелла (см. сводную таблицу в § 3.4.6) в удобном для нашей задачи виде:

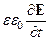= [Ñ, H]- j; 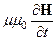= - [Ñ, E].

Так как энергия электромагнитного поля определяется квадратом напряженностей E² и H², умножим первое уравнение скалярно на E, второе – на H. Сложим полученные результаты, получим:

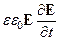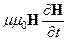+ = E[Ñ, H] - H[Ñ, E] - j E, (93)

где: 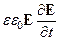= 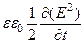и 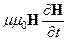= 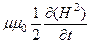(т.к. E² = E² и H² = H²) и

E[Ñ, H] - H[Ñ, E] = -Ñ[E, H] (или E rot H - H rot E= - div [E, H]).

СоотношениеE[Ñ, H] - H[Ñ, E] = -Ñ[E, H] получено с учетом правила смешанного произведения и операции ротора векторных функций [Ñ, H] и [Ñ, E] (проверьте).

Напомним правило смешанного (скалярно-векторного) произведение трех векторов а[b, c]. Смешанное произведение допускает циклическую (стековую) перестановку векторов:а[b, c] =c[а, b] =b [c,а].В результате смешанного произведения получаем скалярную величину. Так какi[j,j] = 0, i[k, k] = 0, i[i, k]=0, i[k,i] = 0 и т.д., то получим:а[b, c] = a_xb_yc_z -a_xb_zc_y + a_yb_zc_x - a_yb_xc_z + a_zb_xc_y - a_zb_yc_x .

Геометрически смешанное произведение равно объему параллелепипеда, построенного на векторах а, bиc. Действительно, скалярное произведение вектора а на вектор[b, c] выражается соотношением а[b,c] = a÷[b,c]çcosa , где модуль векторного произведение ÷[b,c]ç численно равен площади параллелограмма со сторонами b и c, а высота параллелепипеда определяется отношением h = a cosa (рис. 3-39).

Рис. 3-39. Геометрический смысл смешанного произведения а[b, c].

Итак, уравнение (93) принимает вид:

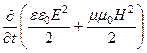= -Ñ[E, H] -j E.

Проинтегрируем полученное выражение по всему выделенному объему V, получим:

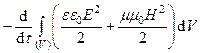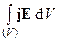= + . (94)

Выражение в левой части (94) – это скорость изменения энергии электромагнитной волны, взятая с обратным знаком, т.е. ( ).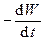

Преобразуем первый объемный интеграл в правой части (94) в поверхностный интеграл по теореме Гаусса-Остроградского:

= ,

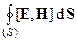где: S – поверхность, охватывающая объем V; П = [E, H] – плотность потока электромагнитной энергии через единичную поверхность – вектор Пойнтинга. Интеграл 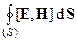º 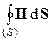– есть поток электромагнитной энергии через поверхность S.

Интеграл Q = 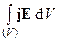- теплота, выделенная в объеме V в проводящих объектах, содержащихся в этом объеме. Теплота Q всегда положительная по знаку. Итак, приходим к уравнению закона сохранения энергии в электромагнитном поле (92):

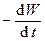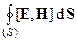= + Q или 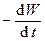= 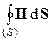+ Q (95)

Приведем две оценки потока энергии через замкнутую поверхность.

1. Пусть 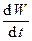> 0, т.е. энергия электромагнитной волны в выделенном объеме возрастает. В этом случае 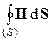= - ( 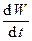+ Q) < 0. Поток вектора Пойнтинга отрицательный, т.е. в этом случае энергия втекает в объем V. Энергия втекающего электромагнитного поля частично компенсирует потери на нагревание проводников в объеме V, а остальная часть энергии идет на увеличение энергии электромагнитного поля в этом объеме.

2. 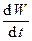< 0 - энергия электромагнитной волны в выделенном объеме V уменьшается. Так как исходная энергия поля всегда больше поглощаемой энергии проводниками (тепло выделяется за счет энергии поля), то 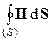= - ( 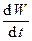+ Q) > 0. таким образом, в этом случае из объема V происходит излучение электромагнитной волны во внешнюю среду.

3.7.3. Поток энергии электромагнитного поля вдоль подводящих

проводов, поглощение энергии в проводах (постоянный ток)

Вначале в первых двух пунктах параграфа рассмотрим подробнее физику осуществления постоянного тока в проводнике.

1. Электрическое поле в объеме однородного проводника при существовании электрического тока в проводнике. В объеме уединенного заряженного проводника электрическое поле отсутствует. Данный факт, как было отмечено ранее, является следствием закона Кулона – закона обратного квадрата.

Ясно, что постоянный электрический ток в проводнике может быть обусловлен существованием электрического поля Eвнутри проводника. Плотность тока j в линейном проводнике определяется законом Омаj = gE, где g – проводимость проводника.

На рис. 3-40 часть проводника, по которому течет постоянный ток плотностьюj. В объеме проводника существует электрическое поле напряженностью E= E_{t, провод.} (нормальная составляющая в объеме проводника отсутствует E_{n, провод.} = 0). ПолеE_t порождает постоянный ток j.

Источником поля E_{t, провод.} внутри проводника не могут быть заряды на клеммах источника тока. Например, в случае длинных проводов на больших расстояниях от клемм источника тока кулоновская сила становится ничтожно малой, однако ток существует. Таким образом, заряды на клеммах не могут быть непосредственными источниками поляE_{t, провод.} внутри проводника.

Так как единственным источником поля E_t внутри проводника, по которому течет постоянный ток,могут быть заряды, то возникает вопрос: где эти заряды находятся? Эксперимент показывает, что после включения источника тока на поверхности проводника всей цепи возникают поверхностные неподвижные заряды, которые и порождают поле E_t в объеме проводника. В качестве экспериментальной установки можно вспомнить, например, известную установку (рис. 3-41-а): поместим в ванну слой диэлектрического порошка и на порошок уложим участки проводов а и б, расположенные достаточно близко друг к другу. При включении цепи (ключ К) крупинки диэлектрического порошка укладываются вдоль силовых линий электрического поляE, созданного поверхностными зарядами. Силовые линии E электрического поля в пространстве между участками а и б показаны на рис. 3-41-б. Вблизи поверхности проводника (вне объема проводника) напряженность поля E поверхностных зарядов направлена под углом к проводнику.

Из граничного условия (57) следует, что тангенциальная составляющая поля вне проводника равна тангенциальной составляющей в объеме проводника: E_{t, диэл.} = E_{t, провод.}. Поле внутри проводника имеет только тангенциальную (касательную) составляющую вдоль проводника E= E_t в направлении электрического тока, а нормальная к поверхности проводника компонента поля внутри проводника отсутствует E_{n, провод.} = 0.

Итак, роль зарядов на клеммах источника тока состоит в создании неподвижных зарядов на поверхности проводника (поверхностных зарядов) по всей длине цепи. Именно эти поверхностные заряды и создают полеE_t в объеме проводника, которое, в свою очередь, порождает электрический ток плотностью j в замкнутой цепи.

2. Электрическое поле в объеме неоднородного проводника при существовании электрического тока в проводнике. В однородных проводниках при включении источника постоянного тока в проводах возникают только поверхностные заряды, объемные заряды в проводнике отсутствуют. На практике, как правило, имеют дело с неоднородными проводниками, в которых проводимость g изменяется от точки к точке проводника, т.е. проводимость является функцией координат - g(x, y, z). Неоднородности могут быть обусловлены разными факторами, например, упругими напряжениями в материале проводника при его деформации, микроскопическими посторонними включениями в материале проводника и т.п. В неоднородном проводнике кроме поверхностных зарядов на неоднородностях в объеме проводника образуются объемные заряды. В общем случае этими объемными зарядами могут быть как связанные заряды с плотностью r ^/, так и свободные заряды с плотностью r_своб.. Эти объемные заряды с объемной плотностью r = r ^/ + r_своб совместно с поверхностными зарядами создают поле E в проводнике.

Покажем, что объемные заряды обеспечивают реализацию постоянного тока в неоднородном проводнике. Представим интегральный закон сохранения заряда (20) в дифференциальной форме.

Закон сохранения заряда (уравнение непрерывности) в интегральной форме (20) можно записать в виде:

= .

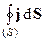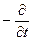
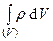По теореме Гаусса-Остроградского 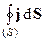= 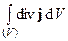, следовательно, имеем:

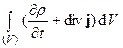= 0.

Ясно, что подынтегральное выражение также равно нулю во всех точках объема V:

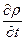+ div j= 0 или 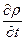+ Ñj = 0. (96)

Уравнение (96) выражает закон сохранения заряда (уравнение непрерывности) в дифференциальной форме.

В случае постоянного тока 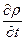= 0, т.к. в этом случае заряд в любом выделенном объеме проводника не изменяется. Поэтому при постоянном токе div j= 0 или Ñj= 0. (97)

Уравнение (97) означает, что линии вектора плотности тока jв цепи постоянного тока замкнуты, т.е. постоянный ток возможен только при замкнутой цепи.

Плотность объемных зарядов r выразим по теореме Гаусса в дифференциальной форме: ÑE = 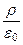. По закону Ома E= 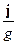, следовательно, можно записать

Ñ( 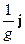) = 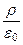, (98)

где вследствие неоднородности проводника проводимость проводника является функцией координат g(x, y, z).

По правилу дифференцирования произведения двух функций – в данном случае скалярной функции 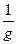и векторной функции j - имеем:

Ñ( 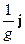) = 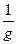Ñj + jÑ( 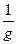) или div( 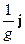) = 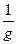divj + jgrad( ).

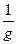С учетом (97) уравнение (98) примет вид:

jgrad( 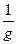) = 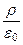(99)

Возьмем прямолинейный участок цепи и направим ось 0X вдоль этого участка. Для простоты допустим, что проводимость изменяется только в направлении оси 0X, т.е. g = g(x). В этом случае градиент примет вид:

grad( ) = .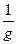

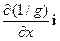Уравнение (99) запишется как j×i 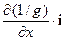= 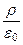(i – орт в направлении оси 0X). Окончательно имеем:

j 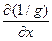= 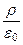. (100)

Из уравнения (100) получаем, что если, например, проводимость g(x) в положительном направлении оси 0X уменьшается (удельное сопротивление r = 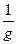растет), то объемный заряд r имеет положительный знак. Это приводит к увеличению напряженности поля E за счет положительных объемных зарядов, что и обеспечивает поддержание постоянной плотности тока j. Аналогично, при увеличении проводимости возникают отрицательные объемные заряды.

3. Поток энергии электромагнитного поля вдоль подводящих проводов, поглощение энергии в проводах.

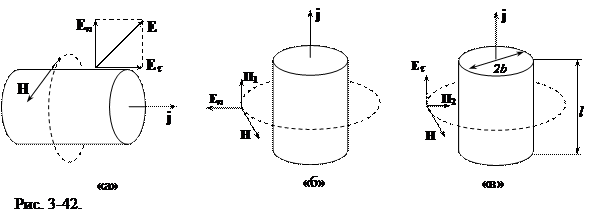
Рассмотрим участок проводника с электрическим током (рис. 3-42-а). Силовые линии магнитного поля тока образуют концентрические окружности (на рисунке показана одна силовая линия). Вектор напряженности H магнитного поля у поверхности проводника направлен по касательной к поверхности проводника. Напряженность электрического поля E у поверхности проводника имеет нормальную E_n и тангенциальнуюE_t составляющие: E= E_n + E_t. Составляющая E_t направлена в ту же сторону, как и ток. Вектор Пойнтинга можно записать в виде:

П₁ = [E, H] = [E_n, H] + [E_t, H].

Введем обозначения: П₁ = [E_n, H] и П₂ = [E_t, H], П = П₁ + П₂.

Исходя из правила определения направления результата векторного произведения следует, что вектор Пойнтинга П₁ = [E_n, H] направлен вдоль проводника и определяет величину электромагнитной энергии, переносимой от источника тока вдоль проводника (рис. 3-42-б). Подчеркнем, поток энергии, определяемый векторомП₁, переносится не в объеме проводника, а вдоль проводника в диэлектрической среде, окружающий проводник. Проводник играет роль только направляющей оси потока электромагнитной энергии.

Вектор Пойнтинга П₂ = [E_t, H] направлен вглубь объема проводника. Вектор П₂ определяет энергию, входящую в проводник. При постоянном токе энергия, определяемая потоком П₂, полностью переходит во внутреннюю энергию материала проводника, приводящая к его нагреванию.

Итак, электромагнитная энергия переносится от источника тока к нагрузке вдоль проводов и определяется нормальной составляющей E_n у поверхности проводника. Тангенциальная составляющая E_t ответственна за потери энергии электромагнитного поля в проводнике.

Как известно, мощность тепла, выделяемого при нагревании проводника, может быть рассчитана по закону Джоуля-Ленца: P = I²R. Покажем, что закон Джоуля-Ленца следует из выражения для вектора Пойнтинга П₂ = [E_t, H], определяющий потери электромагнитной энергии в проводящих объектах. Тем самым опосредованно покажем, что и закон Джоуля-Ленца является следствием уравнениями Максвелла.

Выделим цилиндрический участок проводника диаметром 2b и длиной l (рис. 3-42-в). Поток мощности (поток энергии в единицу времени), втекающий в этот участок проводника через его внешнюю поверхность площадью S = 2pbl, определится интегралом

P = 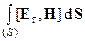= E_t H 2pbl,

где E_t = 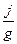, H = 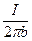- напряженность электрического и магнитного полей соответственно у поверхности проводника. Имеем: P = .

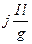По определению модуль плотности тока j = 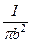. Подставим эту формулу в последнее уравнение, получим:

P = 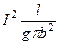= I²R.

Таким образом, поток электромагнитной энергии, вошедший в проводник, равен теплоте, выделенной в проводнике по закону Джоуля-Ленца.

4. Двухпроводная линия передачи электромагнитной энергии (постоянный ток)

На рис. 3-43-а приведена простая схема постоянного тока с источником ЭДС x, соединительных проводов и нагрузки R как потребителя энергии, поступающей от ЭДС. У поверхности соединительных проводов напряженность поля поверхностных зарядов направлена под углом к проводам. Если сопротивление проводов ничтожно мала (близка к нулю), то у поверхности проводов есть только нормальная составляющая поля E_n, а тангенциальная практически равна нулю E_t = 0. Наоборот, у нагрузки R основной компонентой являетсяE_t, а нормальной можно пренебречь E_n = 0.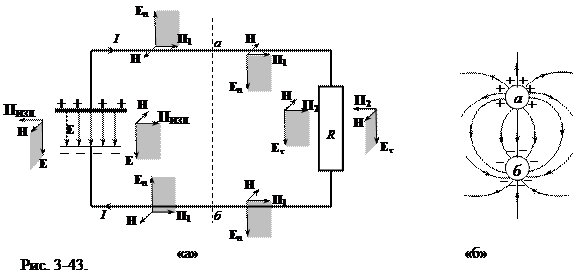

Вектор напряженности E электрического поля в источнике постоянного тока направлен от положительной клеммы к отрицательной. Ток I во внешней цепи течет по часовой стрелке. Допустим, сопротивление подводящих проводов близко к нулю. Силовые линии электрического поля между проводами в сечении а-б (рис. 3-43-б) в этом случае перпендикулярны поверхности проводов (вектор E_t). Направление вектора напряженности магнитного поля H определяется правилом правого винта.

Рассматривая направление векторов E_tи H вблизи поверхности подводящих проводов, убеждаемся, что вектор Пойнтинга П₁ направлен от источника постоянного тока к нагрузке R. Направление вектора П₁ не зависит от направления тока I: и по нижней и по верхнейпо рисунку ветви поток энергии направлен к потребителю энергии R. Впрочем, независимость направления вектораП₁ от направления тока должно быть понятно и из самых общих представлений о законах природы – эти законы не должны зависеть от субъективного (договорного) выбора положительного направления тока.

Вблизи нагрузки R вектор Пойнтинга П₂ направлен в объем нагрузки. Вошедшая в нагрузку энергия электромагнитного поля может превращаться в другие виды энергии: например, в плитке электромагнитная энергия превращается во внутреннюю энергию нагрузки с выделением тепла; в электрическом двигателе – в механическую энергию вращения ротора двигателя и т.д.

В источнике питания поток электромагнитной энергии П_ИЗЛ. направлен от источника во внешнюю среду, излучается во внешнюю среду.

Итак:

1) энергия от источника тока к нагрузке распространяется вдоль подводящих проводов в диэлектрической среде, окружающий провод. Подводящие провода служат направляющей осью распространения потока электромагнитной энергии от источника (генератора) к нагрузке;

2) у нагрузки энергия входит в нагрузку. Реальные подводящие провода обладают конечным сопротивлением, поэтому в линии передачи часть энергии входит в объем подводящих проводов и выделяется в виде тепла. В линии передачи происходят потери, определяемые тангенциальной составляющей E_t электрического поля зарядов на поверхности подводящих проводов;

3) из источника питания поток электромагнитной энергии П_ИЗЛ. выходит («излучается») во внешнюю среду.

Заметим, изложенная выше картина перемещения энергии от генератора к нагрузке во всех линиях передачи в принципе похожи. Различия в линиях, разумеется, есть. Например, при передаче по линии переменных электромагнитных полей усложняется картина силовых линий полей; в зависимости от частоты волны явно или неявно изменяется элементная база линии.

3.7.4. Идеальная двухпроводная линия передачи электромагнитной

энергии(переменные ток)

1. Волновое уравнение напряжения и тока в цепи переменного (квазистационарного) тока. Выделим в цепи переменного тока элемент идеальной линии передачи длиной dx (рис. 3-44). В идеальной линии потери отсутствуют (R = 0). Переменный ток создает переменный магнитный поток, и линия характеризуется некоторой индуктивностью на единице длины L₀. Провода образуют конденсатор с емкостью C₀ на единице длины линии.

На длине dx линии индуктивность L = L₀dx, емкость C = C₀dx. Напряжение на длине dx изменяется на величину 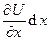, ток на 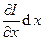. По закону явления самоиндукции имеем: 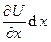= - (L₀ dx) 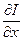или

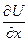= - L₀ 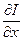. (101)

Входное напряжение элемента цепи равно U. Часть тока 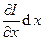идет на зарядку конденсатора до напряжения U, и конденсатор приобретает заряд q = C₀dxU. Имеем: dI = 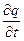= 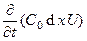. Имеем: - 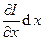= 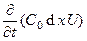или

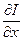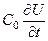- = . (102)

Дифференцируя уравнение (101) по x, а уравнение (102) – по t, получим волновое уравнение напряжения:

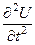= L₀C₀ 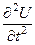. (103)

Дифференцируя уравнение (101) по t, а уравнение (102) – по x, получим волновое уравнение тока:

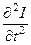= L₀C₀ 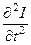. (104)

Итак, колебания носителей заряда в линии передачи порождают волны напряжения и тока. Скорость распространения волны напряжения и тока в линии передачи определяется погонной индуктивностью (магнитной «инерцией») и емкостью (способностью накапливать энергию) линии:

v = 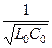. (105)

2. Волновое сопротивление линии передачи. Отражение волны на нагрузке. Решение уравнений типа (103) и (104) ранее было получено, и имеют для волны, распространяющейся в положительном направлении x, вид

U = U₀ cos[ 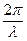(vt – x)] и I = I₀ cos[ 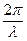(vt – x)]. (106)

Если волна распространяется в одном направлении (например, положительном относительно x), то волна напряжения и волна тока согласно (106) находятся в фазе. В этом случае энергия от генератора все время поступает в линию передачи. Амплитуды напряжения U₀ и тока I₀ по всей линии передачи постоянны (потерь нет!). Это аналогично тому, что наблюдается в цепи постоянного тока без потерь. Вектор напряженности поверхностных зарядов перпендикулярны поверхности проводов линии передачи, тангенциальная составляющая отсутствует E_t = 0.

Подставим решения волновых уравнений (106) в (101), получим:

U = vL₀ I.

Отношение Z₀ = 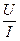= v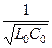L₀ = L₀ = 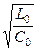(Ом) (107)

измеряется в единицах сопротивления.

Величина Z₀ = 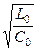называется волновым сопротивлением линии передачи. Обратите внимание, Z₀ не зависит от длины линии, т.к. величины L₀ и C₀ относятся к единице длины линии. Волновое сопротивление Z₀ является собственной характеристикой линии передачи.