Волновое уравнение плоской волны в газе и жидкости
Волновое уравнение плоской продольной волны в газе и жидкости имеет, разумеется, тот же вид, что и уравнение струны. Напомним, плоской волной называется волна, волновые поверхности которой представляют собой плоскость. В поле продольной акустической волны элементы среды испытывают периодические сжатия и разряжения, что приводит к периодическим измерениям давления в элементах среды.
Давление в произвольный момент времени t в элементе среды:
P = p0 + dp,
где: dp - приращение давления (избыточное давление) в данной точке среды в поле акустической волны, которое периодически изменяется во времени; p0 - давление в среде в отсутствии волны.
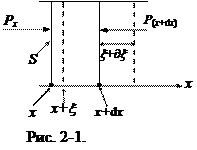 Все точки среды на волновой поверхности колеблются в фазе. Пусть плоская волна распространяется в положительном направлении оси 0x. Выделим элемент среды в виде цилиндра с малой высотой dx и площадью основания S, совпадающей с волновой поверхностью (рис. 2-1). В начальный момент левый торец цилиндра выделенного цилиндра имеет координату x, правый – координату (x + dx). За время dt левый торец сместится на малую величину x, правый – на x + ¶x. Здесь ¶x – абсолютная деформация выделенного элемента среды (на рис.2-1 показано растяжение элемента). Запишем 2-й закон Ньютона для выделенного элемента среды.
Все точки среды на волновой поверхности колеблются в фазе. Пусть плоская волна распространяется в положительном направлении оси 0x. Выделим элемент среды в виде цилиндра с малой высотой dx и площадью основания S, совпадающей с волновой поверхностью (рис. 2-1). В начальный момент левый торец цилиндра выделенного цилиндра имеет координату x, правый – координату (x + dx). За время dt левый торец сместится на малую величину x, правый – на x + ¶x. Здесь ¶x – абсолютная деформация выделенного элемента среды (на рис.2-1 показано растяжение элемента). Запишем 2-й закон Ньютона для выделенного элемента среды.
Масса элемента Dm = rSdx. Под действием результирующей сил давления слева и справа возникает деформация объема: левый и правый торца сместятся на разные расстояния – левый на величину x, правый на величину (x + ¶x). Относительная деформация объема среды:
e = 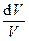 =
= 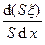 =
= 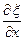 (т.к. S = const).
(т.к. S = const).
Смещение выделенного объема равно x. Таким образом, элемент среды приобретает ускорение ax = 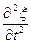 . Сила давления в плоскости с координатой x равна Fx = PxS; в плоскости (x + dx) - F(x+dx) = P(x+dx) S = (Px +
. Сила давления в плоскости с координатой x равна Fx = PxS; в плоскости (x + dx) - F(x+dx) = P(x+dx) S = (Px + 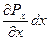 )S. Результирующая сила [Px – P(x+dx)]S = -
)S. Результирующая сила [Px – P(x+dx)]S = - 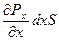 . Теперь запишем закон динамики для выделенного элемента среды:
. Теперь запишем закон динамики для выделенного элемента среды:
rSdx 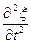 = -
= - 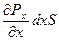 или rSdx
или rSdx 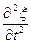 = -
= - 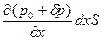 . Окончательно:
. Окончательно:
r 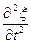 = -
= - 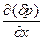 . (1)
. (1)
Определим связь между избыточным давлением dp и относительной деформацией элемента среды 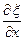 . Динамический эффект сжимаемости (растяжения) объема среды под действием сил давления характеризуется модулем всестороннего сжатия K =
. Динамический эффект сжимаемости (растяжения) объема среды под действием сил давления характеризуется модулем всестороннего сжатия K = 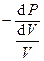 . Приращение давления dP просто равно dp. Поэтому K =
. Приращение давления dP просто равно dp. Поэтому K = 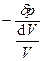 =
= 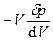 . Знак минус указывает, что увеличение давления приводит к уменьшению объема и наоборот - уменьшение давления приводит к увеличению объема. Избыточное давление
. Знак минус указывает, что увеличение давления приводит к уменьшению объема и наоборот - уменьшение давления приводит к увеличению объема. Избыточное давление
dp = 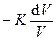 =
= 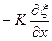 .
.
Подставим полученное соотношение в уравнение (1), получим:
r 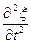 = -
= - 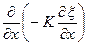 или r
или r 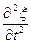 = K
= K 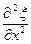 .
.
Запишем последнее уравнение в форме
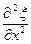 =
= 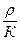
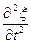 . (2)
. (2)
Уравнение (2) есть волновое уравнение плоской акустической волны в среде, в которой отсутствуют потери. Отношение 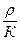 имеет размерность обратного квадрата скорости, т.е., как и в волновом уравнении для струны,
имеет размерность обратного квадрата скорости, т.е., как и в волновом уравнении для струны, 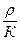 =
= 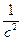 . Итак,
. Итак,
фазовая скорость акустической волны
c = 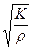 . (3)
. (3)
Фазовая скорость определяется упругими и инертными свойствами среды. Теперь волновое уравнение можно записать в виде
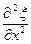 =
= 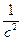
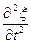 . (4)
. (4)
Решение уравнения (4) (см. главу 1, §1.2.1):
x = x0 cos (wt – kx). (5)
В комплексной форме решение запишется в виде
x = x0 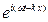 (5*)
(5*)
Скорость акустической волны в газе и жидкости. Модуль всестороннего сжатия K определяется характером процесса сжатия. Вследствие относительно малой теплопроводности газов и жидкостей Пуассон предположил, что сжатие (разряжение) элементов газа происходит адиабатически. Уравнение адиабатического процесса в идеальном газе
PVg = const.
Имеем: Vg dP + g P V g-1 dV = 0 или 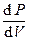 =
= 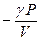 .
.
Следовательно, адиабатический модуль всестороннего сжатия газа («жесткость» газа)
Kад = 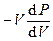 = gP или Kад = g(p0 + dp).
= gP или Kад = g(p0 + dp).
В акустическом поле обычных звуковых волн добавочное изменение давления порядка dp ~102Па, а атмосферное давление p0 ~105Па, поэтому можно принять: P = p0 + dp » p0.
Плотность среды r = r0 + dr » r0.
Итак, адиабатическую «жесткость» газа можно считать равным
Kад = gp0.
Заметим, изотермическая «жесткость» KТ = p0, которая получается из закона Бойля-Мариотта. Адиабатическая жесткость газа в g = 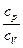 раз больше изотермической жесткости.
раз больше изотермической жесткости.
Таким образом, скорость звука в хорошем приближении можно рассчитывать по формуле:
c = 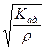 =
= 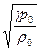 - где p0 – атмосферное давление.
- где p0 – атмосферное давление.
Например, для воздуха, который состоит в основном из двухатомных молекул – азота N2 и кислорода O2, показатель адиабаты g = 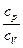 = 1,4. Рассчитанное значение скорости при нормальном атмосферном давлении равно 340 м/с, что хорошо согласуется с экспериментальными данными. Согласование расчетных и экспериментальных данных наблюдается и для других газов (при не очень высоких частотах акустической волны). Можно считать, что сжатие и разряжение элементов газовой среды в поле акустической волны при не очень высоких частотах является практически адиабатическим процессом.
= 1,4. Рассчитанное значение скорости при нормальном атмосферном давлении равно 340 м/с, что хорошо согласуется с экспериментальными данными. Согласование расчетных и экспериментальных данных наблюдается и для других газов (при не очень высоких частотах акустической волны). Можно считать, что сжатие и разряжение элементов газовой среды в поле акустической волны при не очень высоких частотах является практически адиабатическим процессом.
Уравнение смещения имеет вид (5*), тогда уравнение относительной деформации среды примет вид e = 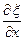 = - ikx0
= - ikx0 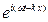 = - ikx. (6)
= - ikx. (6)
Уравнение скорости смещения
vx = 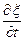 = iwx0
= iwx0 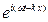 = iwx. (7)
= iwx. (7)
Уравнение избыточного давления
dp = 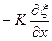 = K ikx0
= K ikx0 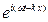 = i K kx. (8)
= i K kx. (8)
Обратите внимание, скорость и избыточное давление колеблются в фазе.
Акустический импеданс среды есть отношение избыточного давления dp к скорости элементов следы:
Z = 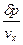 =
= 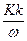 =
= 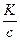 = r0c, т.к. c =
= r0c, т.к. c = 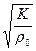 . (9)
. (9)
Уравнение (8) можно записать в виде dp = Z vx = i r0cwx0 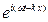 = r0cv0x
= r0cv0x 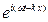 .
.
В среде всегда наблюдается поглощение энергии акустической волны. Механизмами поглощения энергии средой являются процессы переноса в среде при распространении волны – теплопроводность, диффузия, вязкость. Уравнение затухающей волны имеет вид (см. главу 1, §1.2.6)
x = x0 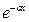 cos (wt – kx)
cos (wt – kx)
В комплексной форме решение запишется в виде x = x0 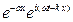 .
.
Коэффициент затухания в газах и жидкостях пропорционален квадрату частоты a = bn2. При небольших частотах коэффициент поглощения a = 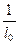 мал. Например, при частоте звука n = 103 Гц в воздухе l0 = 5×104 м. Однако, при частоте ультразвука n = 5×105 Гц ультразвуковая волна в воздухе затухает практически около излучателя (l0 » 3×10-2м). Отсюда следует, что скорость распространения волны также зависит от частоты.
мал. Например, при частоте звука n = 103 Гц в воздухе l0 = 5×104 м. Однако, при частоте ультразвука n = 5×105 Гц ультразвуковая волна в воздухе затухает практически около излучателя (l0 » 3×10-2м). Отсюда следует, что скорость распространения волны также зависит от частоты.
Для жидкостей уравнение состояния в явном виде не удается представить и, в этой связи, теоретический расчет адиабатического модуля всестороннего сжатия не представляется возможным. Для жидкостей Kад обычно определяют по экспериментальным значениям скорости звука. Для жидкостей Kад ~ 1010 Н/м2. Коэффициент затухания в жидкостях на несколько порядков меньше, чем в газе. Например, для воды на частоте n = 105 Гц величина l0 » 3×103 м.
