Глава 3 Сложение колебаний

Одна и та же точка может одновременно участвовать в двух или более движениях. Вспомните, хотя бы, движение тела брошенного под углом к горизонту: тело двигается равномерно и прямолинейно по горизонтали и равноускоренно и прямолинейно по вертикали. Результирующая траектория – парабола.

Аналогичная ситуация складывается и с колебательными системами. Тело может одновременно участвовать в нескольких колебаниях. Например, подвешенный на нити шарик можно поочередно заставить колебаться то в одной вертикальной плоскости, то в другой, перпендикулярной первой. Но можно заставить его одновременно колебаться в этих плоскостях. Для этого шарик, колеблющийся в одной плоскости, надо ударить в направлении, перпендикулярном этой плоскости. Два колебания во взаимно перпендикулярных плоскостях «сложатся», и перед наблюдателем предстанет результирующее движение (в данном случае по эллипсу).

Задача заключается в определении результата наложения нескольких колебаний.

Во многих случаях при наложении колебаний выполняется принцип суперпозиции, суть которого заключается в том, что при наложении колебания не искажают друг друга. Это означает, что суммарное смещение колеблющегося тела вдоль какой-либо координатной оси равно алгебраической сумме смещений во всех колебаниях:

Допустим, что тело участвует одновременно в двух колебаниях вдоль одной прямой:

Видно, что колебания происходят вдоль одной прямой ОХ, их частота w одинакова, отличаются только амплитуды А и В и начальные фазы колебаний. Нетрудно понять, что в результате наложения тело будет двигаться вдоль прямой ОХ, а его координата в любой момент времени

Найти сумму двух гармонических функций одной частоты можно алгебраически, но удобнее и, главное, нагляднее это сделать геометрически.

§1 Метод векторных диаграмм

Вращение вектора

Пусть вектор расположен так, что его начало совпадает с началом отсчета на оси ОХ и сам вектор составляет угол j₀ с положительным направлением оси ОХ.

Очевидно, что проекция вектора на ось ОХ, являющаяся катетом в треугольнике, равна

Будем вращать вектор вокруг точки О с постоянной угловой скоростью w. При этом проекция вектора на ось ОХ будет изменяться. При повороте вектора на угол wt он будет составлять с положительным направлением оси ОХ угол (wt + j₀). Тогда проекция будет равна

Интересно, что проекция вектора меняется по гармоническому закону, то есть колеблется с циклической частотой w. Этот факт можно использовать для графического представления колебания. Гармоническое колебание величины изображают вектором 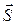, длина которого равна амплитуде колебания , а угол между вектором и горизонтальной осью ОХ – начальной фазе колебаний .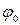

Вращение двух векторов

Рассмотри два вектора и 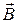с общим началом в точке О. В начальный момент эти вектора составляют с положительным направлением оси ОХ углы и соответственно.

Будем вращать вектора и 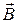с одинаковой угловой скоростью w. Очевидно, что взаимная ориентация векторов относительно друг друга меняться не будет, между ними всегда будет угол .

Построим по правилу параллелограмма сумму векторов . Нетрудно видеть, что при вращении векторов и 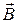их сумма – вектор – тоже будет вращаться с той же угловой скоростью, не меняя своей ориентации относительно и . Параллелограмм векторов вращается как единое целое.

Посмотрим, как ведут себя проекции векторов. Как было показано ранее, проекции вращающихся векторов колеблются с циклической частотой w:

С другой стороны, как видно из рисунка, проекция вектора равна сумме проекций векторов и :

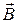(1)

где - угол, который вектор составляет с положительным направлением ОХ в начальный момент.

Нетрудно видеть, что сумма двух гармонических функций одной частоты есть гармоническая функция той же частоты .

Рассмотрим обратную задачу

Пусть требуется найти сумму двух гармонических функций

Если А ¹ В, то решить задачу алгебраически непросто (вынести числовой коэффициент за скобки и воспользоваться формулой суммы косинусов нельзя). Это не значит, что алгебраически решить задачу нельзя! Но есть прием, который существенно упрощает работу. Достаточно вспомнить два предыдущих примера.

Сумма двух гармонических функций одной частоты есть тоже гармоническая функция той же частоты - смотри выражение (1). Ответ можно записать сразу!! Задача сводится к нахождению амплитуды результирующей функции С и ее начальной фазы .

Заменим алгебраическую задачу на геометрическую: будем складывать не гармонические функции, а вектора. Для это сделаем следующее:

· Построим ось ОХ, отметим на ней точку О.

· Построим вектор с началом в точке О длины А, повернутый относительно оси на угол .

· Построим вектор 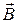с началом в точке О длины В, повернутый относительно оси на угол .

· Построим вектор по правилу параллелограмма.

· Найдем длину вектора по теореме косинусов – это будет амплитуда результирующей функции.

(2)

(3)

· Найдем угол, который вектор составляет в начальный момент с положительным направлением оси ОХ.

Итак, задача решена

Где значения С и могут быть найдены по формулам (2) и (3).

Рассмотрим самый простой пример. Найдите сумму

Заметим, что sina = cos(a - p/2) . Тогда

· Строим вектор длиной 3 единицы (его направление может быть произвольным), для простоты расположим этот вектор горизонтально.

· Строим вектор 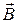: его начало совпадает с началом А, длина вектора равна 4 единицам, он повернут относительно вектора А на угол -p/2. Помним, что положительные углы мы отсчитываем против часовой стрелки, а отрицательные – по часовой стрелке.

· Сумму векторов находим по правилу параллелограмма.

· Модуль вектора легко найти по теореме Пифагора

·

Для угла проще всего найти тангенс

Окончательный результат

Возвращаемся к физике

При наложении двух колебаний одной частоты, происходящих вдоль одной прямой мы будем видеть не два движения, а одно. Тело будет совершать колебания вдоль оси ОХ с той же частотой w, изменятся лишь амплитуда и начальная фаза результирующего колебания.

Амплитуда результирующего колебания, как мы показали ранее, зависит не только от амплитуд накладываемых колебаний, но и от разности начальных фаз складываемых колебаний.

1 Пусть j₀₁ - j₀₂ = 2pk, где k = 0, 1, 2,… Такие колебания называются синфазными. На векторной диаграмме это выглядит так: