Параметрическое программирование
Существует значительная группа экономических задач, в которых в состав линейной целевой функции или правой части ограничивающих условий входит параметр. Например, если эффективность или доход зависят от сезонных колебаний, тогда критерий оптимальности должен эту зависимость отображать. Если снабжение ресурсов также изменяется под влиянием каких-то причин, то в системе ограничений это должно отобразиться. Если продукция, которая изготовлена предприятием, должна некоторое время сохраняться, то ее стоимость состоит из двух частей: постоянной – это стоимость продукции на момент изготовления – и переменной части, которая зависит от срока хранения, причем эта зависимость, как правило, линейная. Целевая функция задачи оптимального планирования такого производства будет иметь коэффициенты, которые линейно зависят от параметра 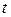 (от времени).
(от времени).
Главная идея метода решения таких задач состоит из двух частей:
§ берут фиксированную величину параметра 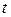 (а именно
(а именно 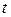 равняется самому меньшему значению
равняется самому меньшему значению 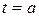 ); тогда все коэффициенты функции цели будут постоянными; решают задачу для этого случая, то есть находят вершину, в которой достигнут экстремум;
); тогда все коэффициенты функции цели будут постоянными; решают задачу для этого случая, то есть находят вершину, в которой достигнут экстремум;
§ определяют все значения параметра 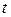 , для которых оптимальное решение сохраняется, то есть для которых экстремальное значение достигается в одной и той же точке. Найденные значения исключают из интервала изменения параметра
, для которых оптимальное решение сохраняется, то есть для которых экстремальное значение достигается в одной и той же точке. Найденные значения исключают из интервала изменения параметра 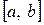 ; для оставшегося интервала вновь решают задачу.
; для оставшегося интервала вновь решают задачу.
Эти две части метода повторяют до тех пор, пока не будут найдены решения для всех 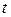 . Более детально алгоритм будет таким:
. Более детально алгоритм будет таким:
1. Задачу готовят к решению: функцию устремляют к минимуму; неравенства преобразуют в уравнения, вводя дополнительные переменные; вводят искусственные переменные, если нужно.
2. Присваивают параметру 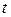 наименьшее значение из отрезка
наименьшее значение из отрезка 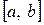 . Соответственно с этим конкретизируют целевую функцию.
. Соответственно с этим конкретизируют целевую функцию.
3. Строят І симплексную таблицу в соответствии с правилами.
4. Дополняют І симплекс-таблицу двумя строками. В 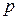 -строке записывают с противоположным знаком коэффициенты целевой функции, не связанные с параметром
-строке записывают с противоположным знаком коэффициенты целевой функции, не связанные с параметром 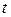 . В
. В 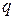 -строку вносят с противоположным знаком коэффициенты функционала, которые стоят перед параметром
-строку вносят с противоположным знаком коэффициенты функционала, которые стоят перед параметром 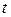 .
.
5. Проводят расчеты всех элементов таблицы в соответствии с правилами симплексного метода, проверяя оптимальность на основе М-строки, а потом 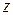 -строки.
-строки.
6. Выписывают оптимальное решение, если критерий эффективности выполнился. После этого строка 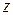 во внимание не берется.
во внимание не берется.
7. Находят для 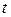 интервал постоянства решения, рассматривая такие случаи (
интервал постоянства решения, рассматривая такие случаи ( 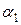 - начало интервала,
- начало интервала, 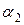 - конец интервала):
- конец интервала):
а) все 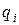 положительные
положительные 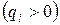 - в этом случае частичный интервал определяется следующим образом:
- в этом случае частичный интервал определяется следующим образом:
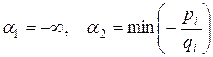
б) все 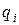 отрицательные
отрицательные 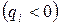 - в этом случае интервал постоянства решения находится так:
- в этом случае интервал постоянства решения находится так:
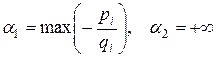
в) 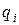 принимают как положительные, так и отрицательные значения – в этом случае интервал постоянства решения будет таким:
принимают как положительные, так и отрицательные значения – в этом случае интервал постоянства решения будет таким:
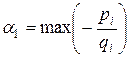 для
для 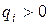
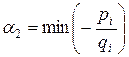 для
для 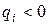
8. Если полученный интервал не охватывает отрезок 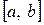 , то необходимо продолжить поиск и найти решения для других значений
, то необходимо продолжить поиск и найти решения для других значений 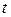 .
.
9. Следующий этап заключается в выборе ключевого столбца – им будет столбец, в котором получено значение 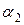 . Далее выполняют симплекс-преобразование и определяют новый частичный интервал
. Далее выполняют симплекс-преобразование и определяют новый частичный интервал 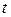 для нового решения. Эту процедуру повторяют до тех пор, пока будет исчерпан весь отрезок
для нового решения. Эту процедуру повторяют до тех пор, пока будет исчерпан весь отрезок 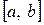 .
.
Пример.
Найти решение задачи параметрического программирования
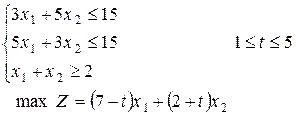
Подготовим задачу к решению:
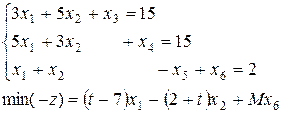
где 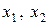 | - основные переменные, |
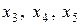 | - дополнительные переменные, |
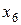 | - искусственная переменная. |
Присвоим параметру 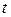 наименьшее значение из его интервала и конкретизируем целевую функцию:
наименьшее значение из его интервала и конкретизируем целевую функцию: 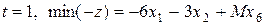
Сформируем 1 симплекс-таблицу с дополнительными строками:
Таблица 1
| Базис | С | 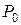 | – 6 | – 3 | М | С.О. | |||
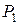 | 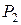 | 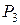 | 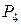 | 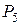 | 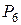 | ||||
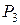 | |||||||||
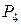 | |||||||||
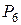 | М | – 1 | |||||||
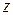 -строка -строка | |||||||||
| М-строка | -1 | ||||||||
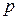 -строка -строка | |||||||||
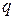 -строка -строка | -1 |
Критерий оптимальности не выполняется.
В таблице 1 ключевыми будут столбец 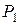 и третья строка. В базис входит вектор
и третья строка. В базис входит вектор 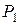 , выходит искусственный вектор
, выходит искусственный вектор 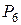 . Генеральный элемент равен 1.
. Генеральный элемент равен 1.
Таблица 2
| Базис | С | 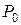 | – 6 | – 3 | С. О. | |||
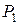 | 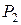 | 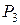 | 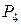 | 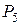 | ||||
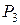 | ||||||||
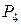 | – 2 | |||||||
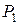 | – 6 | – 1 | – | |||||
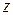 -строка -строка | – 12 | – 3 | ||||||
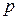 -строка -строка | – 14 | – 5 | ||||||
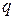 -строка -строка | – 1 |
В таблице 2 критерий оптимальности не выполняется. В новый базис входит 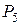 , выходит из базиса
, выходит из базиса 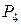 . Генеральной элемент равен 5.
. Генеральной элемент равен 5.
Таблица 3
| Базис | С | 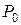 | – 6 | – 3 | С.О. | |||
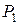 | 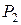 | 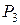 | 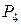 | 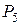 | ||||
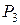 | 16/5 | – 3/5 | 15/8 | |||||
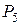 | – 2/5 | 1/5 | – | |||||
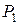 | – 6 | 3/5 | 1/5 | |||||
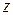 -строка -строка | – 18 | – 3/5 | – 6/5 | |||||
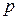 -строка -строка | – 21 | – 11/5 | – 7/5 | |||||
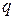 -строка -строка | 8/5 | 1/5 |
В таблице 3 достигнут минимум 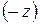 и максимум
и максимум 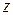 . Оптимальные значения основных переменных такие:
. Оптимальные значения основных переменных такие:
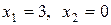 .
.
Это решение определяет вершину 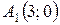 . Оно будет сохраняться для определенных значений
. Оно будет сохраняться для определенных значений 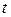 . Поскольку все
. Поскольку все 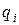 положительны, то мы имеем случай а) пункта 7:
положительны, то мы имеем случай а) пункта 7:
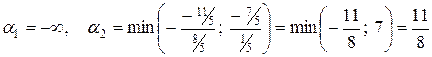 .
.
Значит, вершина 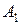 обеспечивает максимум для
обеспечивает максимум для 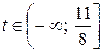 . Этот интервал не перекрывает отрезок
. Этот интервал не перекрывает отрезок 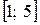 , поэтому решение надо продолжить. Ключевым столбцом будет столбец
, поэтому решение надо продолжить. Ключевым столбцом будет столбец 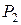 , так как именно в нем получено значение
, так как именно в нем получено значение 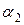 . В новый базис включаем
. В новый базис включаем 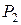 , выключаем
, выключаем 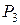 , генеральный элемент равен
, генеральный элемент равен 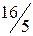 . Все расчеты выполняем в соответствии с правилами симплексного метода. Получим таблицу 4.
. Все расчеты выполняем в соответствии с правилами симплексного метода. Получим таблицу 4.
Таблица 4
| Базис | С | 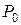 | – 6 | – 3 | С.О. | |||
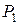 | 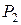 | 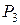 | 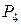 | 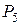 | ||||
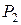 | -3 | 30/16 | 5/16 | – 3/16 | – | |||
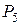 | 28/16 | 2/16 | 2/16 | |||||
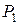 | – 6 | 30/16 | -3/16 | 5/16 | ||||
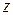 -строка -строка | – 270/16 | 3/16 | – 21/16 | |||||
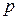 -строка -строка | – 270/16 | 11/16 | – 29/16 | |||||
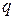 -строка -строка | -8/16 | 8/16 |
В таблице 4 получено новое решение:
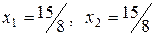 .
.
Оно определяет вершину 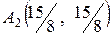 . Эта вершина будет обеспечивать оптимальность для других значений
. Эта вершина будет обеспечивать оптимальность для других значений 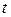 , которые находятся на основе случая в) пункта 7, так как величины
, которые находятся на основе случая в) пункта 7, так как величины 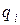 имеют разные знаки:
имеют разные знаки:
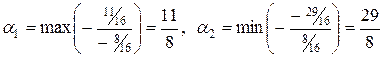 .
.
Таким образом, в точке 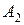 достигается максимум, если
достигается максимум, если 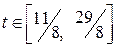 . Этот интервал тоже не охватывает значения отрезка
. Этот интервал тоже не охватывает значения отрезка 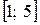 , необходимо двигаться дальше, искать решения для оставшихся значений
, необходимо двигаться дальше, искать решения для оставшихся значений 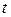 . Ключевым станет столбец
. Ключевым станет столбец 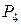 , вектор
, вектор 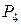 войдет в базис, выйдет из базиса вектор
войдет в базис, выйдет из базиса вектор 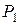 , генеральный элемент равен
, генеральный элемент равен 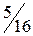 . Получим таблицу 5.
. Получим таблицу 5.
Таблица 5
| Базис | С | 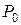 | – 6 | -3 | |||
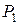 | 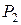 | 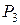 | 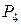 | 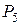 | |||
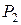 | – 3 | 3/5 | 1/5 | ||||
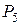 | – 2/5 | 1/5 | |||||
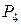 | 16/5 | – 3/5 | |||||
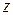 -строка -строка | – 9 | 21/5 | – 3/5 | ||||
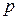 -строка -строка | – 6 | 29/5 | – 3/5 | ||||
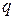 -строка -строка | – 3 | – 8/5 | – 1/5 |
В таблице 5 получено такое решение: 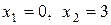 . Оно отвечает вершине
. Оно отвечает вершине 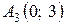 . Поскольку все
. Поскольку все 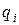 отрицательные, то вершина
отрицательные, то вершина 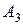 , в соответствии со случаем б) пункта 7, будет оптимальной для следующих значений
, в соответствии со случаем б) пункта 7, будет оптимальной для следующих значений 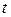 :
:
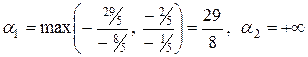 .
.
Подводя итоги, конкретизируем выводы:
§ если 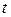 принадлежит интервалу
принадлежит интервалу 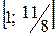 , то целевая функция достигает максимума в точке
, то целевая функция достигает максимума в точке 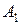 ;
;
§ если 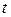 принимает значение из интервала
принимает значение из интервала 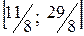 , то максимум будет в вершине
, то максимум будет в вершине 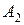 ;
;
§ если 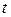 изменяется от
изменяется от 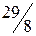 до 5, то максимум достигается в точке
до 5, то максимум достигается в точке 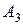 .
.
Если дать геометрическую интерпретацию результатам решения, то получим такую картину. Пятиугольник 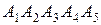 является множеством допустимых решений системы ограничений. С учетом отрезка изменения параметра
является множеством допустимых решений системы ограничений. С учетом отрезка изменения параметра 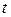 максимум сначала достигается в вершине
максимум сначала достигается в вершине 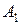 , потом – в вершине
, потом – в вершине 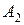 , а в конце – в вершине
, а в конце – в вершине 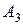 .
.
| 3. Задания для самостоятельного решения |
