Механический и геометрический смысл производной

Пусть на интервале (а,b) задана непрерывная функ­ция у=f(x).

Её график называют непрерывной кривой.

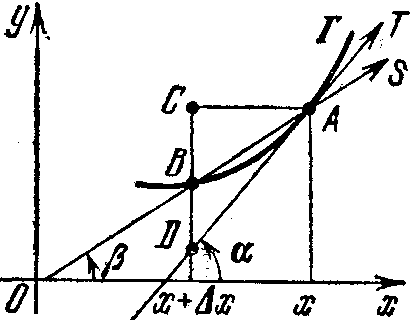
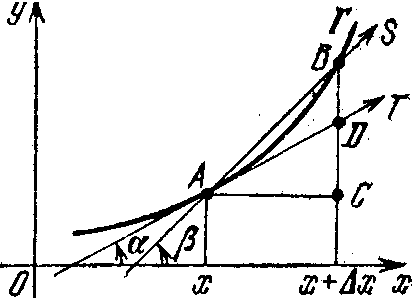
Обозначим его через Г. Зададим на Г точку А=(х,f(х))и поставим целью определить касательную к Г в этой точке. Для этого введем на Г другую точку B=(x+Dx,f(x+Dx)), где Dx¹0 (рис. 1 изобра­жён случай Dx>0, а на рис. 2 – случай Dx<0). Пря­мую, проходящую через точки А и В, направленную в сторону возрастания х (отмеченную стрелкой), наз. секущей и обозначим через S. Угол, который S образует с положительным направлением оси х, обозначим через b. Мы считаем, что –p/2<b< p/2. При b>0 угол отсчи­тывается от оси x против часовой стрелки, а при b<0 по часовой стрелке. На данных рисунках b>0. На рис. 1 Dx=AC, Dy=СВ, а на рис. 2 Dx=–AC, Dy=–СВ, В обоих случаях Dy/Dx=tgb.

Если Dx®0, то Dy®0 и точка В, двигаясь по Г, стремится к A. Если при этом угол b стремится к некоторому значению a, отличному от p/2 и –p/2, то суще­ствует предел lim_Dx®0Dy/Dx=lim_b®atgb=tga , равный производной (конечной) от f в точке x: f'(x)=tga. Обратно, если существует (конечная) производная f'(x), то b®a=arctg f'(x). При стремлении b к a секущая S стремится занять положение направленной прямой Т, проходящей через точку А и образующей угол a с положительным направ­лением оси х. Направленная прямая Т наз. касательной к кривой Т в её точке А. Определение: Касательной к кривой Г (y=f(x)) в её точке А=(х,f(х)) наз. направленная пря­мая Т, к которой стремится секущая S (направленная в сторону возрастания х прямая), проходящая через А и точку В=(x+Dx,f(x+Dx))ÎГ, когдаDx>0. Мы доказали, что если непрерывная, функция у=f(х) имеет конечную производную f'(х) в точке х, то её гра­фик Г в соответствующей точке имеет касательную с угловым коэффициентом tga=f'(х) (–p/2<a<p/2). Обратно, существование предела limb=a(–p/2<a<p/2) влечет за собой существование конечной производной f'(х) и справедливость равенств (1), (2). Может случиться, что f имеет в точке х правую и левую производные, отличные между собой: f'(x)¹f'_пр(x).

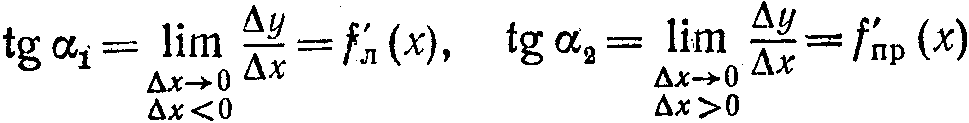
Тогда А есть угловая точка Г. В этом случае касательная к Г в A не существует, но можно говорить, что суще­ствуют правая и левая касательные с разными угловыми коэффициентами: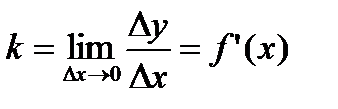

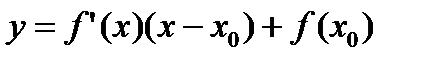- уравнение касательной

Физический смысл производной.

Скорость движения точки есть производная пути по времени.

V(t)=S’(t)

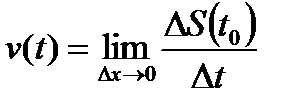-формула мгновенной скорости

Замечательные пределы. Число e.

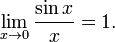Согласно нашему правилу нахождения пределов пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе, очевидно, тоже ноль. Таким образом, мы сталкиваемся с неопределенностью вида 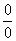, которую, к счастью, раскрывать не нужно. В курсе математического анализа, доказывается, что: 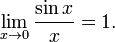Данный математический факт носит название Первого замечательного предела.

Нередко в практических заданиях функции могут быть расположены по-другому, это ничего не меняет:

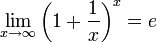или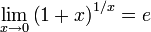

Доказательство второго замечательного предела:

Доказательство для натуральных значений

Докажем вначале теорему для случая последовательности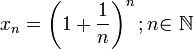

По формуле бинома Ньютона:

Полагая 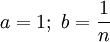, получим:

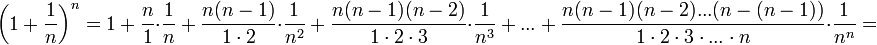
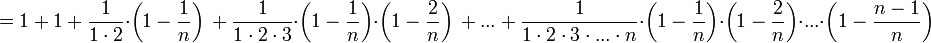(1)

Из данного равенства (1) следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число убывает, поэтому величины 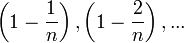возрастают. Поэтому последовательность 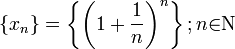— возрастающая, при этом

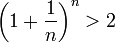(2).

Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство

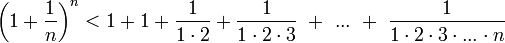
Усилим полученное неравенство, заменим 3,4,5, …, стоящие в знаменателях дробей, числом 2:

.

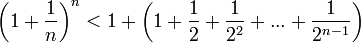Сумму в скобке найдём по формуле суммы членов геометрической прогрессии:

.

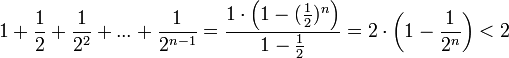Поэтому 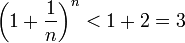(3).

Итак, последовательность ограничена сверху, при этом 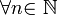выполняются неравенства (2) и (3): .

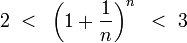Следовательно, на основании теоремы Вейерштрасса (критерий сходимости последовательности) последовательность 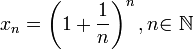монотонно возрастает и ограниченна, значит имеет предел, обозначаемый буквой e. Т.е.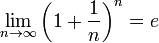

Леммы о бесконечно малых:

1. Для того чтобы переменная 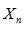имела своим пределом постоянное число a, необходимо и достаточно выполнения равенства:

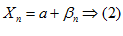
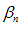– бесконечно малая величина.

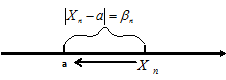
Результат следует из того, что разность 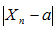есть расстояние от точки 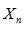до её предела 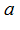, это расстояние стремится к нулю, т. к. 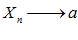, и наоборот: если расстояние стремиться к нулю, то .

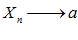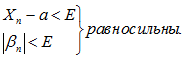
2. Алгебраическая сумма конечного числа бесконечно малых, есть величина бесконечно малая.

Доказательство:

Рассмотрим, например, сумму 3-х бесконечно малых.

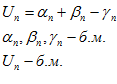
Возьмем любое E > 0, т. к. 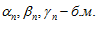,то по определению существует номер n такой, что будет выполняться три неравенства:

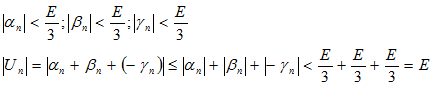
(по лемме №2 о вещественных числах).

Существует номер n,такой, что при n > N выполняется неравенство:

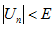для 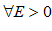, это и означает, что 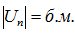, Ч. Т. Д.

Опр. 2:Переменная 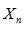называется ограниченной, если существуют такие m и M , что для всех 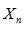выполняется неравенство: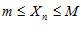

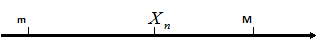
ПРИМЕР:

1. sin(n) – ограниченное, т. к. |sin n| ≤ 1

2.

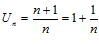
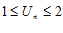
3.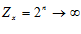 –не является ограниченным.

(О. П. – ограниченная переменная).

ЛЕММА №3:Произведениеограниченнойпеременной набесконечно малуюесть величинабасконечно малая

Пусть

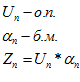
Требуется доказать, что: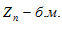

Доказательство:

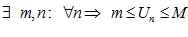
Пусть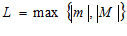

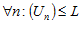
Возьмем 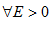, т.к. 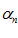– бесконечно малая, то существует номер N такой что при: ,

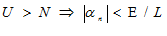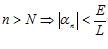
Тогда 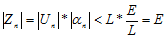. 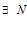, при 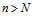, следовательно, выполняется неравенства: ,

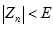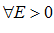
Это и означает, что: 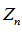– бесконечно малая.