Обратная угловая засечка

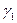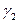Обратная угловая засечка – это задача по определению координат четвертого пункта (Р₂) по координатам трех исходных пунктов (ст.1, ст.2 и ст.3) и двум горизонтальным углам, измеренным при определяемом пункте ( и ) (рис. 2.3).

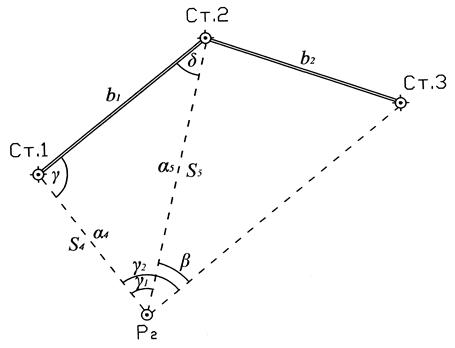
Рис. 2.3. Схема обратной угловой засечки

Дано: , ;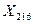

, ;

, .

, .

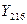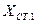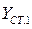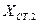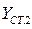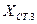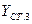Измерено: , .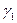

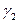Найти: , .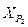

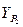Направления с пункта Р₂ на исходные пункты (ст.1, ст.2, ст.3) измерены тахеометром методом круговых приемов (одним полным приемом). Результаты измерений представлены в табл. 12.

Таблица № 12

Результаты измерений горизонтальных углов методом круговых приемов

Направление	Круг	Отсчет по горизонтальному кругу		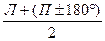	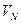Приведенное направление Ni
ст.1	Л	0°09'05"			0°00'00"
П	180°09'02"
ст.2	Л	48°02'37"
П	228°02'25"
ст.3	Л	74°48'24"
П	254°48'31"
ст.1	Л	0°09'12"
П	180°09'12"
Незамыкание горизонта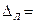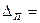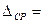

Вычислить в журнале измерений горизонтальных углов (табл. 12):

– поправки в направления:

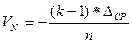, где

k – номер направления (при этом начальное направление принимается за первое);

n – число направлений в приеме (n=3);

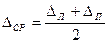– среднее значение незамыкания горизонта.

– горизонтальные углы:

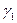= N _ст.2 – N _ст.1,

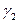= N _ст.3 – N _ст.1, где

N _ст.i – приведенные направления.

Порядок вычислений

2.4.1. По известным координатам пунктов ст.1, ст.2 и ст.3 (табл. 6) найти длины базисов 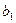и 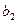, дирекционные углы 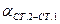и 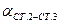из решения обратной геодезической задачи.

2.4.2. Вычислить угол :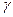

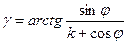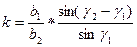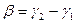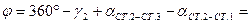
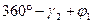, где

;

;

, где .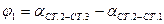

2.4.3. Из решения треугольника Ст.1–Ст.2–Р₂ найти 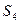и :

;

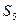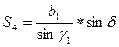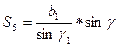, где

.

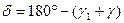2.4.4. Вычислить дирекционные углы 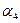и :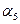

;

.

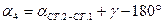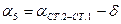2.4.5. Вычислить координаты определяемого пункта Р₂:

;

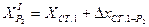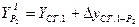, где

,

.

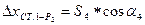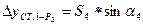2.4.6. Контроль вычисления координат определяемого пункта Р₂:

;

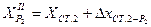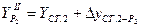, где

,

.

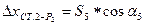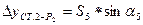2.4.7. Контроль считается выполненным, если координаты определяемого пункта P₂ совпадут.

Если контроль выполняется, то записать окончательные значения координат определяемого пункта 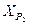и .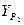

Вычисления выполнить в табл. 13.

2.4.8. Оценка точности результатов измерений и координат определяемого пункта Р₂.

– Используя полученные координаты 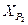и 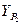решить обратную геодезическую задачу и вычислить 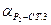и .

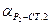– Найти значения горизонтального угла β^выч:

.

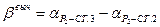– Вычислить угловую невязку и сравнить её с допустимой угловой невязкой:

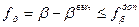, где

,

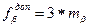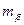– СКП измерения горизонтального угла ( ).

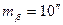– Оценка точности положения определяемого пункта P₂:

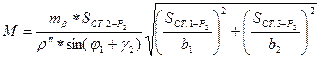, где

S_i – находят из решения обратной геодезической задачи, используя координаты 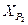и .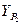

Таблица № 13

Вычисление координат пункта Р₂

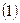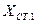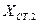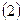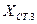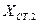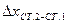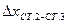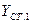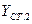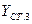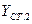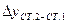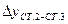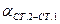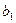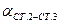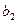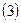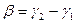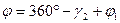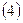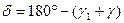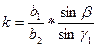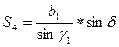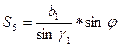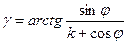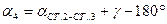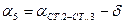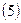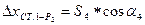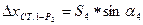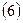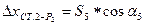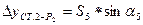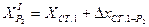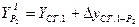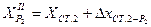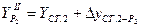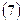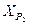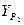Линейная засечка

Линейная засечка – это задача по определению координат пикета (Скважина) по координатам двух исходных пунктов (ст.1, Р₂) и двум расстояниям от определяемого пункта до исходного ( 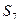и 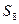) (рис. 2.4). Для контроля определения пикета Скважина, от третьего исходного пункта (ст.2) было измерено расстояние .

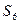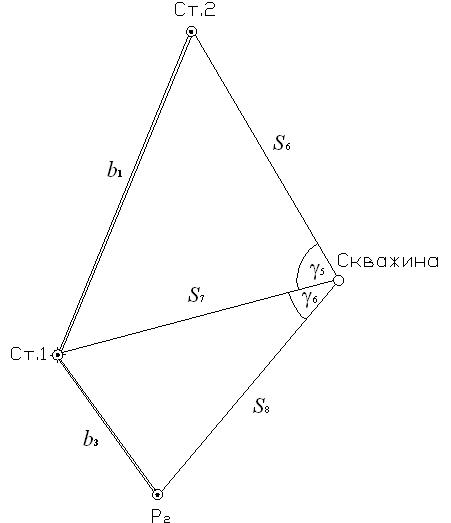
Рис. 2.4. Схема линейной засечки

Дано: , ; , ; , .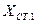

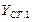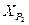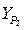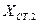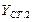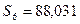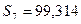Измерено: (м);

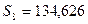(м);

(м).

Найти: , .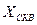

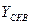Порядок вычислений

2.5.1. По известным координатам пунктов ст.1, ст.2 и P₂ (табл. 6 и табл. 13) найти длины базисов 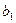и 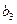из решения обратной геодезической задачи.

2.5.2. Вычислить координаты пикета Скважина:

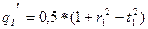, где

;

;

.

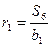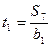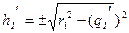В данном случае пункты ст.2, Скважина, ст.1 следуют походу часовой стрелки, следовательно при вычислении 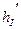будет знак «+».

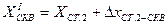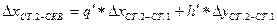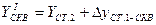, где

;

, где

.

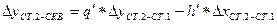2.5.3. Повторное вычисление координат пикета Скважина:

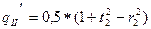, где

;

;

.

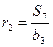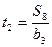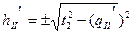В данном случае пункты Р₂, Скважина, ст.1 следуют по ходу часовой стрелки, следовательно при вычислении 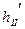будет знак «+».

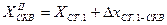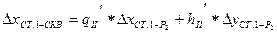, где

;

, где

.

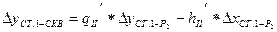Вычисления выполнить в табл. 14.

2.5.4. Контроль вычислений.

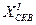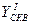– Используя полученные координаты и решить обратную геодезическую задачу и найти значение .

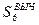– Вычислить линейную невязку и сравнить её с допустимой:

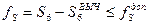, где

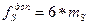
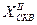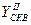– Используя полученные координаты и решить обратную геодезическую задачу и найти значение .

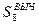– Вычислить линейную невязку и сравнить её с допустимой:

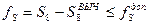, где

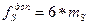
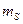– СКП измерения расстояни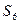й и 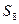(для электронного тахеометра ).

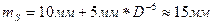2.5.5. Оценка точности положения определяемого пункта:

– Из решения обратной геодезической задачи найти 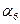и , и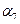спользуя полученные координаты 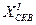и .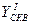

– Вычислить СКП положения пикета из первого решения:

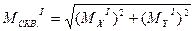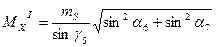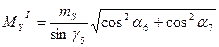, где

,

, где

угол на определяемом пикете .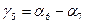

– Из решения обратной геодезической задачи найти 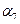и , и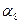спользуя полученные координаты 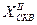и .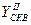

– Вычислить СКП положения пикета из второго решения:

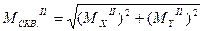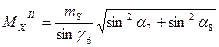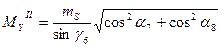, где

,

, где

угол на определяемом пикете .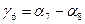

2.5.6. Контроль считается выполненным, если координаты пикета Скважина вычисленные дважды с контролем, отличаются на величину 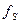, не превышающую :

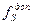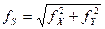, где

, .

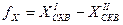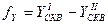Таблица № 14

Вычисление координат определяемого пункта Скважины