Геометрична інтерпретація формули середнього значення

Нехай функція 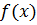– неперервна і невід’ємна на проміжку 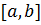. Формула (2) з геометричної точки зору означає, що площа криволінійної трапеції = площі прямокутника за такой ж основою, що і у криволінійної трапеції і з висотою .

Властивість 10. Узагальнена формула середнього значення

Нехай виконані умови:

1. Функція f(x), а також функція 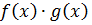– інтегровані на проміжку .

2.

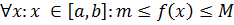
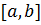3. , тобто на проміжку функція не змінює знак.

Тоді - 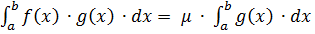(1) ( якщо покласти , отримаємо формулу з вл. 9).

Доведення:

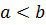і будемо вважати, що . З другої умови теореми випливає, що 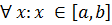виконується нерівність:

(2)

Якщо помножимо нерівність (2) на функцію , то отримаємо:

(3)

З цього слідує, що:

(4)

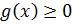Якщо , то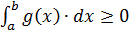

1. Якщ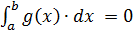о , то . Отже за 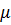ми можемо взяти будь-яке число з ;

2. Якщо 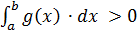. Розділивши нерівность (4) на одержимо: 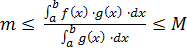(5). Отже, 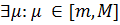. Покладемо у нерівності (5), що Перший випадок доведено.

2) У всіх інших випадках формула (1) залишається правильною, оскільки зміна знаку функції з «+» на «-», а також зміна меж інтегрування на протилежні з 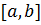на 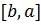не змінює формулу (6).

Зауваження:

Якщо умови теореми виконані і функція 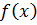неперервна на 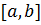, то формулу (1) можна подати у вигляді:

, де .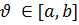

ВИЗНАЧЕНИЙ ІНТЕГРАЛ ЗІ ЗМІННОЮ ВЕРХНЬОЮ МЕЖЕЮ

Зауваження:

У визначеному інтегралі змінну інтегрування можна позначати будь-якою літерою або буквою, тобто має місце рівність::

Нехай функція 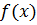інтегрована на 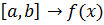буде інтегрована на , де тобто змінна 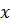– верхня межа.

Визначений інтеграл, що має вигляд 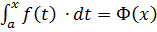називається визначеним інтегралом функції зі змінною верхньою межею.

Властивість 1.

Якщо функція 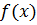інтегрована на проміжку 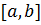, то Ф( неперервна на .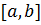

Доведення:

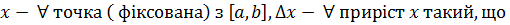
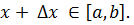
Нехай Введемо позначення

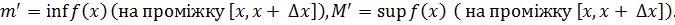
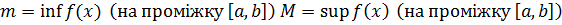
Розглянемо приріст функції .

Якщо застосувати формулу середнього значення, то (*), де .

Якщо в рівності (*) перейти до границі, коли , то одержимо: . А це означає, що функція – неперервна в точці 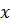. Оскільки точка 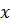була обрана довільно, то Ф – неперервна на .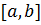

Властивість 2.

Якщо функція – інтегрована на проміжку 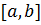і неперервна в точці . Тоді функція Ф диференційована в точці .

Доведення:

Нехай умови нашого твердження виконано тоді з рівності (*) ( властивості 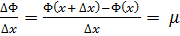1) :

(1)

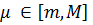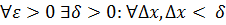Де . Оскільки функція – неперервна в точці , то це означає, що буде виконуватись нерівність:

виконується нерівність а значить і :

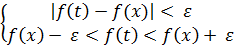
Причому 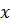– фіксована 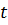– змінна 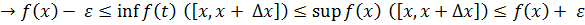(2)

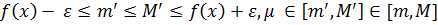
Одержимо ,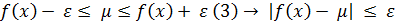

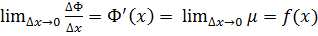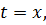Якщо перейти до границі в рівності (1), то одержимо . Це означає, що функція Ф має похідну в точці яка дорівнює .

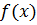Наслідок:

Якщо 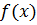– неперервна в 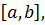то Ф( диференційована на 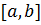. Тобто 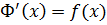. Це означає, що 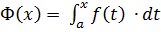можна розглядати як первісну .

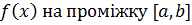ФОРМУЛА НЬЮТОНА-ЛЕЙБНІЦА

Нехай функція 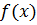– неперервна на 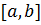, тоді має місце наступна формула Ньютона-Лейбніца:

Де – будь-яка з первісних функції 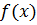на .

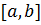Доведення:

Нехай функція 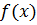– неперервна на 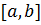, тоді згідно з наслідком до другої властивості інтеграла зі змінно верхньою межею функція 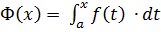є первісною . 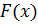– будь-яка інша первісна. Тоді згідно із твердженням про первісні функції одержимо, що:

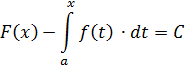
Покладемо :

Покладемо :

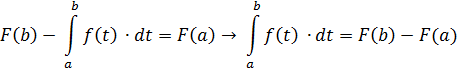
Метод інтегрування частинами

Нехай функції u(x) , v(x), u´(x), v´(x) неперервні на [a,b]. Тоді має місце наступна формула:

- або = - .

Доведення:

За допомогою правила диференціювання добутку можна отримати рівність: Ця рівність означає,що функція є первісною для . Оскільки остання функція є неперервною на проміжку [a,b], то за допомогою формули Ньютона - Лейбніца одержимо, що 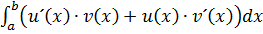= . З останньої рівності безпосередньо випливає формула (1):

= - .

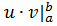Приклад

= = - = =

Заміна змінної у визначеному інтегралі

Теорема

Нехай виконуються умови:

Функція 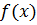неперервна на [a,b].

Функція 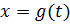, а також неперервні на проміжку [ ]. Причому 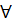t [ 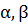] виконується нерівність a ≤ ≤ b, тобто значення функції 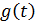не виходить за межі проміжку [a,b].

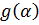=a, =b. Тоді має місце наступна формула:

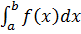= (1)

Доведення

Нехай виконуються умови теореми. Оскільки функція 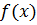неперервна на [a,b], то за допомогою формули Ньютона- Лейбніца, одержимо :

(2), де - будь-яка первісна для 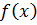. Оскільки 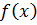неперервна на [a,b], то згідно з наслідком до другої властивості інтеграла зі змінною верхньою межею, цей інтеграл (який є однією з первісних для 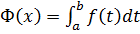) є диференційованою функцією. Тому будь-яка інша первісна, у тому числі , диференційована на [ ], диференційована на проміжку. Тоді диференційована [α,β]. Причому виконується рівність:

=

Остання рівність означає, що 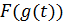- первісна для . Оскільки остання функція є неперервною на проміжку [ ], то згідно з формулою Ньютона – Лейбніца, одержимо наступну рівність:

= (3)

(за третьою умовою теореми)

Порівнюючи рівності (2) і (3) одержимо рівність (1), що і треба було довести.

Якщо при обчисленні визначеного інтеграла зроблена заміна, то при знаходженні цього інтеграла немає потреби повертатися до вихідної заміни.