Образцы выполнения контрольных работ

Задание 2

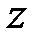Дано комплексное число . Записать число в алгебраической и тригонометрической формах, найти все значения , вычислить .

Решение:

Домножим числитель и знаменатель числ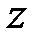а на (сопряженное комплексное число числу ).

= – алгебраическая форма комплексного числа z. Геометрически число изображается как точка с координатами на плоскости или как вектор .

Модуль комплексного числа равен: .

Аргумент комплексного числа определяется из соотношений:

тогда .

x

y

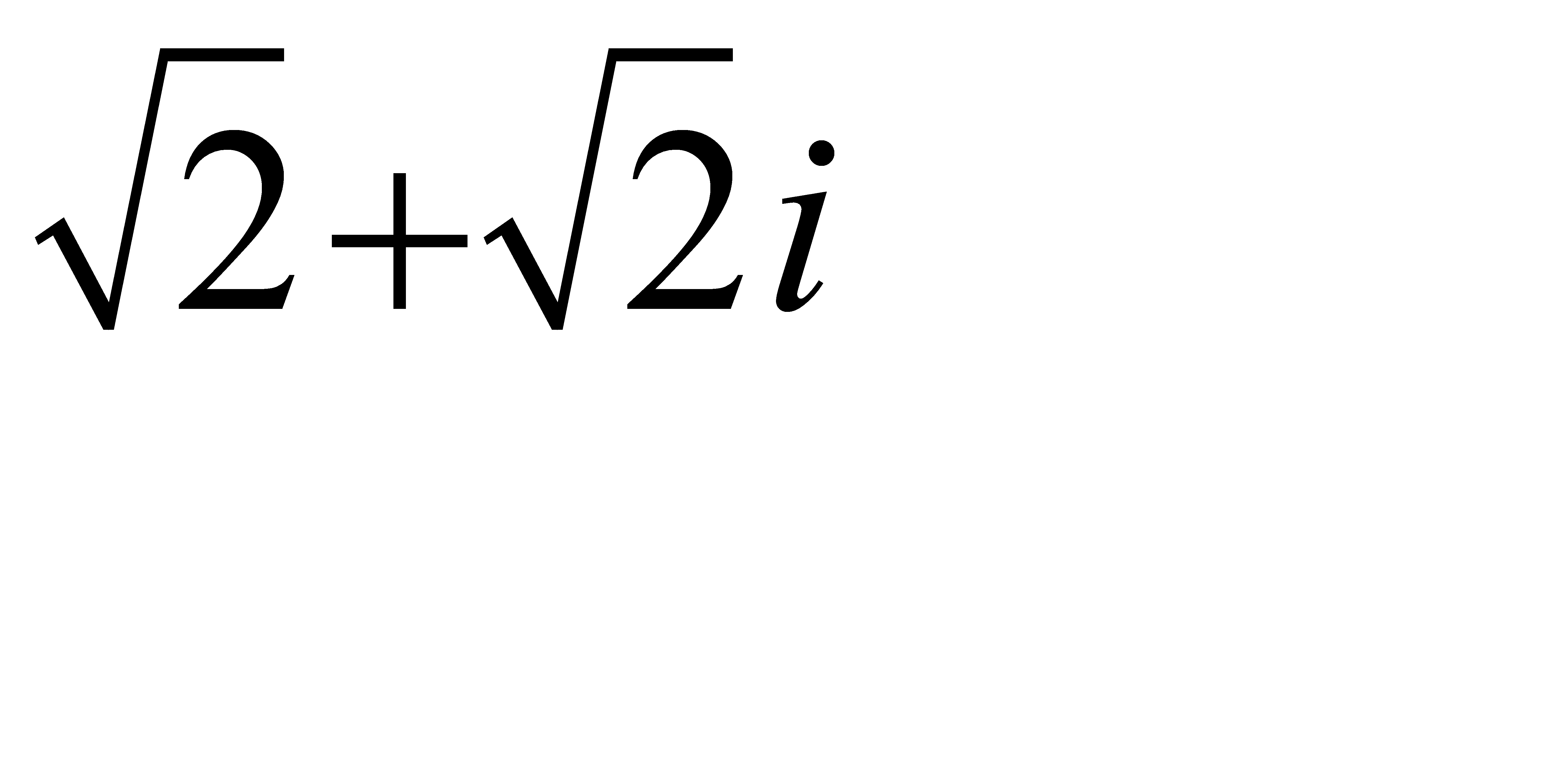
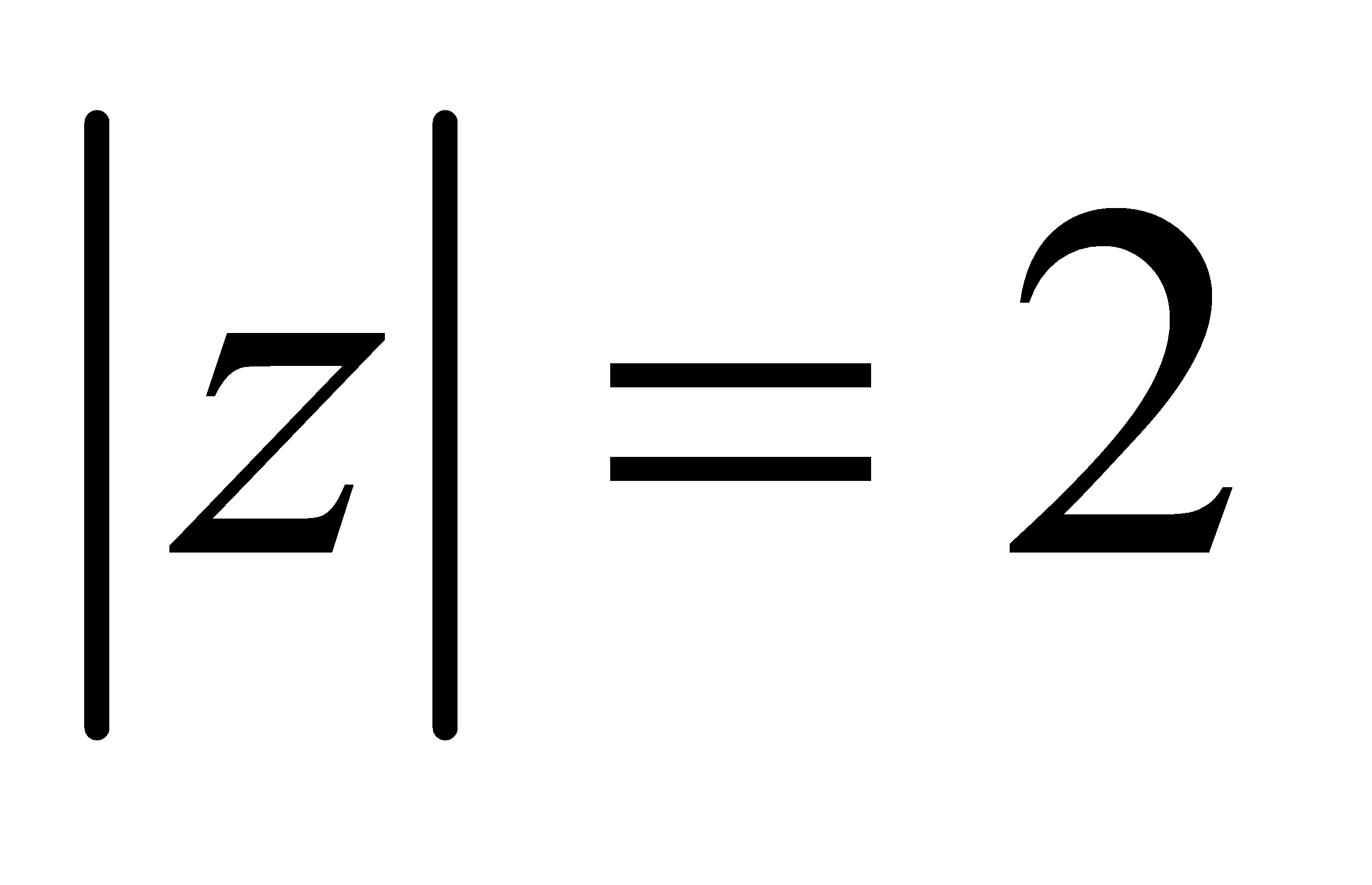
Таким образом, тригонометрическая форма комплексного числа имеет вид:

Значения находим по формуле

, где .

;

;

.

Найдем по формуле Муавра

.

В нашем случае , поэтому

Окончательно получаем:

– тригонометрическая форма числа .

– алгебраическая форма числа .

Задание 3

Вычислить пределы:

1.

2.

3.

4.

5.

.

Задание 4

При решении примеров используются формулы производных сложных функций , где :

и другие.

1. .

2. Преобразуем:

.

.

3.

4.

.

5.

.

Задание 5

Провести полное исследование функций и построить графики.

а) ; б) .

Решение:

а) .

1) Функция определена на всей оси Ох, кроме точки , где она терпит бесконечный разрыв.

2) Находим наклонные асимптоты :

;

Наклонная асимптота . Вертикальная асимптота .

Находим критические точки, в которых первая или вторая производная равна нулю, либо не существует:

;

.

Критическими точками будут и , где =0 . В точке функция не существует.

Из формулы для следует, что y<0 при , и y>0 при .

Из формулы для следует, что при xиз (- ,-2) >0, т.е. функция возрастает; в интервале (-2,-1) <0 – функция убывает, а точка является точкой максимума. В интервале (0,+ ) >0 – функция возрастает. В интервале (-1;0) производная <0 и функция убывает. Точка – точка минимума.

В интервале (- ;-1) <0 – график функции выпуклый, в интервале(-1;+ ) >0 - график вогнутый.

Результаты исследований сведем в таблицу:

x	(- ,-2)	-2	(-2,-1)	-1	(-1,0)		(0,+ )
y	-	-4	-	-	+		+
	+		-	не сущ.	-		+
	-	-	-	не сущ.	+	+	+
Выводы:	Функция возрастает; график выпукл.	Точка максимума	Функция убывает; график выпукл.	Точка разрыва	Функция убывает; график вогнут.	Точка минимума	Функция возрастает; график вогнут.

Строим график:

б) .

1) Функция определена, если >0 , т.е.

В точках и функция имеет бесконечный разрыв, так как:

; .

2) Прямые и – вертикальные асимптоты, т.к. lim|y|= в этих точках.

Наклонные асимптоты:

; ;

Таким образом, уравнение асимптоты .

3) Находим и : ;

.

Критические точки: 0, в точках и функция не существует;

=0 , точка – критическая точка; ОДЗ.

>0 в интервалах (- ;-2) и (1;+ ) – функция возрастает;

<0 в интервале (1;+ ) – график функции выпуклый;

>0 в интервале (- ;-2) – график функции вогнутый;

Из условия у=0 найдем точку пересечения кривой с осью Ох.

.

Составим таблицу, включающую точки и ; .

x	(- ,-2)	-2		(1, ).	.	( ,+ )
y	+	+	-	-		+
	+	не сущ.	не сущ.	+	+	+
	+	не сущ.	не сущ.	-	-	-
Выводы:	Функция возрастает; график вогнут.	Вертикальная асимптота.	Вертикальная асимптота.	Функция возрастает; график выпукл.		Функция возрастает; график выпукл.

Строим график функции:

Задание 6

Найти неопределённые интегралы. В пунктах а) и б) результаты проверить дифференцированием.

а) ; б) ;

в) ; г) .

Решение.

а)

.

Проверка.

Найдём производную от полученного результата:

.

Получили исходную подынтегральную функцию. Значит, интеграл найден верно.

Ответ: .

б) находят интегрированием по частям. Формула интегрирования по частям имеет вид

.

Примем . Первое равенство дифференцируем, второе интегрируем:

.

Получаем: . Применяя формулу интегрирования по частям, находим:

.

Проверка.

.

Интеграл вычислен верно.

Ответ: .

в) – интеграл от рациональной дроби. Найдём корни многочлена, стоящего в знаменателе, т. е. решим уравнение :

и разложим знаменатель дроби на множители, а дробь – на сумму двух простейших дробей:

.

Приравняем числители первой и последней дроби:

.

Это тождество должно выполняться при всех .

Подставим : .

Теперь подставим : .

Значит, разложение дроби имеет вид:

.

Найдём теперь заданный интеграл:

.

Ответ: .

г) В интеграле сделаем замену переменной , откуда . Дифференцируя обе части, найдём:

.

После замены интеграл принимает вид:

=

.

Ответ: .

Задание 7

Вычислить приближённое значение определённого интеграла с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака:

.

Решение.

Для приближённого вычисления определённого интеграла по формуле Симпсона следует:

а) разделить отрезок интегрирования [a, b] на n равных частей точками , , , …, (где n – чётное число). Длина каждой части ;

б) Вычислить функцию в точках деления. Обозначить

.

Формула Симпсона имеет вид

.

Для заданного интеграла .

При , ; , .

= .

Ответ: .

Задание 8

Вычислить определенный интеграл применяя формулу Ньютона-Лейбница:

Решение:

Заданный интеграл является табличным и он равен

= = arcsin1 – arcsin0 =

Ответ:

Задание 9

Вычислить площадь фигуры, ограниченной линиями

.

Решение.

Искомая площадь заштрихована на рисунке.

Её величина вычисляется по формуле

.

Ответ: .

Задание 9

Пример 1. Найти частное решение уравнения х • dх + у • dу = 0, удов­летворяющее начальному условию у(1) = 0 . Выделить интегральную кривую, проходящую через точку М (1,0).

Решение. Разделим переменные: х • dх = - у • dу. Интегрируем:

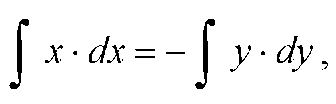получаем 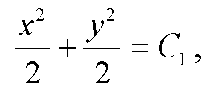или, обозначив 2 С1

через С², будем иметь х² + у² = С² - общий интеграл. Это уравнение семейства концентрических окружностей с центром в начале координат

и радиуса С. Для решения задачи Коши подставим в общий интеграл

начальные условия х = 1, у = 0: 1² + 0² = С² ,откуда

С² = 1, а тогда искомое частное решение х² + у² = 1 (частный инте­грал)- окружность с центром в начале координат радиуса 1. Это инте­гральная кривая, проходящая через точку М (1,0).

Пример 2. Найти общее решение (или общий интеграл) диффе­ренциального уравнения:

(x ² + y ²)dx–xydy = 0 .

Решение. Разделив обе части уравнения на dx, приведём его к ви­ду

или =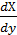

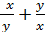
Применив подстановку у = uxу' = u'х + u, найдём:

u'х + u = u + .

Разделяем переменные и интегрируем:

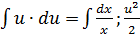=ln│x│+C

Учитывая, что u = , получим: 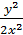, = ln │х│ + C. Это - общий интеграл.

Кроме того, х = 0 - интеграл данного уравнения.

Ответ: 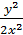, = ln │х│ + C; х = 0

СОДЕРЖАНИЕ