Устойчивость нестационарных систем

Линейными системами с переменными параметрами или нестационарными системами называют системы, процессы в которых описываются линейными дифференциальными уравнениями с переменными во времени коэффициентами

[a₀(t)pⁿ + a₁(t)p^n-1 + .... + a_n(t)]Y(t) = [b₀(t)p^m + b₁(t)p^m-1 + .... + b_m(t)]X(t),

(7.14)

где Y(t) и X(t) – выходная и входная величины; ai(t), bi(t) – переменные коэффициенты, являющиеся известными функциями времени и задаваемые либо графически, либо аналитически; p =d/dt – оператор дифференцирования.

Для нестационарных систем понятие устойчивости имеет некоторую специфику. Действительно, если предположить, что входная величина системы x(t) = x0 = Const и к моменту времени t₁ переходные процессы в системе закончились, т.е. если принять p = d/dt = 0, то из (8.14) для t > t₁ имеем

Y(t) = [b_m(t)/a_n(t)]X0. (7.15)

Из (7.15) видно, что в зависимости от характера изменения коэффициентов a_n(t) и b_m(t) в нестационарной системе даже при постоянной входной величине Х₀ выходная величина Y(t) может изменяться неограниченно долго. Так как время работы реальных систем ограничено, то установившегося значения в нестационарной системе за время ее работы не наблюдается и поэтому понятие асимптотической устойчивости теряет практический смысл. Точные методы исследования устойчивости нестационарных систем довольно сложны, поэтому на практике используются приближенные методы, например, метод замораживания коэффициентов. Он применим в тех случаях, когда нестационарная система работает только в течение ограниченного интервала времени Т, а коэффициенты (7.14) практически не изменяются за время переходного процесса в системе.

В соответствии с этим методом для некоторого фиксированного времени t = t_k определяют соответствующие ему значения a_i(t_k) и b_i(t_k) коэффициентов дифференциального уравнения (7.14), заменяют исходную нестационарную систему некоторой фиктивной стационарной САУ и исследуют устойчивость по любому критерию.

Если полученная таким образом стационарная система устойчива, то считают, что исследуемая нестационарная система тоже устойчива в рассматриваемый момент времени. Затем проводят аналогичное исследование устойчивости для других фиксированных моментов времени, лежащих в интервале 0 ≤ t ≤ T, где Т – время работы.

Если во всем рабочем интервале Т условия устойчивости стационарной системы, полученной методом замораживания коэффициентов, выполняются, то исходную нестационарную систему на этом интервале считают устойчивой.

Степень достоверности метода будет тем выше, чем меньше изменяются коэффициенты за время протекания переходного процесса, а также от правильного выбора фиксированных моментов времени, их количества, с тем чтобы охватить возможные варианты значений коэффициентов, в которых происходит значительное изменение, смена знака и т.д.

В общем случае, когда коэффициенты уравнения (7.14) изменятся значительно, при 8сследовании устойчивости нестационарных систем пользуются понятием технической устойчивости или устойчивости на конечном интервале. Систему считают технически устойчивой на данном интервале Т, если выходная величина Y(t) не превышает некоторой заданной величины Y_доп при 0 ≤ t ≤ T. Y_доп выбирается в каждом конкретном случае из технических соображений (рисунок 7.5).

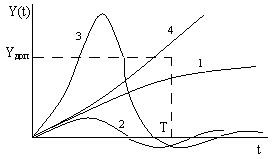
Рисунок 7.5 – Выходные величины нестационарных систем: 1,2 – технически устойчивая система; 3,4 – технически неустойчивая

Определение Y(t) производят обычно при заданном входном воздействии X(t) с помощью различных приближенных аналитических методов, либо методами математического моделирования (например, с помощью программы VisSim).

Контрольные вопросы

1) Какой критерий лежит в основе определения устойчивости по виду ЛАЧХ?

2) Чему равна ПФ запаздывающего звена?

3) Почему для определения устойчивости САУ с запаздыванием алгебраические критерии непригодны?

4) Что такое критическая частота ω_кр системы с запаздыванием?

5) Что такое τ_кр для систем с запаздыванием?

6) Какие линейные системы называются нестационарными?

7) Как определяется устойчивость нестационарной системы?