Затверджено на засіданні кафедри СТ.
Затверджено на засіданні кафедри ІУС.
Протокол № 16 від 29 червня 2011 р.
Затверджено на засіданні кафедри СТ.
Протокол № 17 від 30 червня 2011 р.
Затверджено на засіданні кафедри ШІ.
Протокол № 29 від 30 червня 2011 р.
"Узгоджено"
Завідувач кафедри ІУС _________________проф. Левикін В.М.
(підпис) (П.І.Б.)
Завідувач кафедри СТ _________________проф. Петров Е.Г.
(підпис) (П.І.Б.)
Завідувач кафедри ШІ ________________доц. Рябова Н.В.
(підпис) (П.І.Б.)
Ухвалено вченою радою факультету КН
Протокол №від “ ” 20 р.
Навчальний графік з дисципліни
Дискретна математика
(назва дисципліни)
для напряму 6.050101 „Комп’ютерні науки”
| ВИДИ ЗАНЯТЬ | НАВЧАЛЬНІ ТИЖНІ | ||||||||||||||||||
| Лекції | обсяг, годин | - | |||||||||||||||||
| Лаборат. роботи | обсяг, годин | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |
| Практич ні заняття | обсяг, годин | ||||||||||||||||||
| Самост. робота студентів | обсяг, годин | 35,5 | 31,5 | ||||||||||||||||
| Контроль-ні роботи | КРд | КРа | |||||||||||||||||
| Точки контролю | кт1 | кт2 | кт3 | ||||||||||||||||
| Консультації | |||||||||||||||||||
| Строки проведення заліків, іспитів | ісп |
2 МЕТА І ЗАВДАННЯ ДИСЦИПЛІНИ
2.1 Мета навчальної дисципліни
Метою дисципліни «Дискретна математика» є:
- ознайомлення студентів з основними базовими поняттями, ідеями і методами подання та обробки дискретної інформації;
- надання положень дискретної математики як інструментарію при обробці інформації з використанням сучасної комп’ютерної техніки;
- навчання студентів використанню формальних методів дискретної математики, пов’язаних з розробкою та експлуатацією інформаційних управляючих систем і систем штучного інтелекту, зокрема, їхнього математичного і програмного забезпечень;
- навчання студентів засобам подання дискретних математичних об’єктів і вирішенню типових задач дискретної математики.
2.2. Завдання дисципліни
За результатом вивчання дисципліни студенти повинні:
ЗНАТИ:
- історію розвитку математичного апарату, орієнтованого на формалізацію дискретних процесів;
- методи та засоби дискретної математики в галузі опису та формалізації дискретних процесів (мову теорії множин, відношень, комбінаторного аналізу, елементи булевої алгебри, алгебри висловлювань, алгебри предикатів, теорії графів, основи кодування інформації, основні положення мов і граматик, основи скінчених автоматів);
- основні положення дискретної математики в сфері побудови сучасних пристроїв і систем для обробки дискретної інформації.
ВМІТИ:
- аналізувати логічну та алгоритмічну структуру фізичних і технологічних процесів, процесів обробки інформації в природі та суспільстві;
- використовувати апарат дискретної математики для формалізації та математичного опису задач, що виникають у сфері науки та виробництва;
- виконувати аналіз, синтез і перетворення дискретних об’єктів та процесів, використовуючи поняття і закони теорії множин і теорії відношень, реляційної алгебри, теорії комбінаторного аналізу, математичної логіки;
- використовувати мову графів для опису програмних моделей в інформаційних системах та інформаційних технологіях;
- виконувати синтез та аналіз графових структур та алгоритмів на них;
- вирішувати типові задачі теорії множин і теорії відношень, комбінаторного аналізу, теорії графів, булевої алгебри та математичної логіки.
3. ПЕРЕЛІК ЗАБЕЗПЕЧУЮЧИХ ДИСЦИПЛІН
Основою для вивчення дисципліни «Дискретна математика» є знання з математики у рамках середньої освіти, деяких розділів вищої математики (зокрема, теорії матриць), елементів інформатики.
4. ТЕМАТИЧНИЙ ПЛАН
4.1 Розподіл обсягу змістовних модулів за видами занять
| Но-мер за-лік. кред. | Змі-стов. мод. | Назва та зміст змістовного модуля | Розподіл часу за видами занять, год | Рейтин-гова оцінка | |||
| Лек-ції | Практ. занят | Самостійна робота студентів | |||||
| години | кз | ||||||
| І | 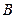 | Введення в дисципліну. | 0,25 | - | 0,625 | - | |
| В.1 | Мета і задачі дисципліни, її місце в системі підготовки фахівців з комп'ютерних наук. | 0,25 | - | 0,125 | - | ||
В.2 (сам. роб.) | Історія зародження, розвитку і становлення дискретної математики. Внесок вчених у її розвиток. | - | - | 0,5 | - | ||
| 1. | Основи теорії множин. Алгебра множин. | 3,75 | 5,875 | - | 3-5 | ||
| 1.1 | Основні поняття і позначення теорії множин.Інтуїтивне поняття множини. Елементи множини. Скінченні та нескінченні множини. Універсальна і порожня множини. Способи задання множин. Потужність множин. Множина і підмножини. | 1,75 | 2,875 | - | 3-5 | ||
| 1.2 | Алгебра множин.Геометрична інтерпретація множин: кола Ейлера та діаграми Венна. Операції на множинах. Загальне визначення алгебри. Поняття алгебри множин. Аксіоми алгебри множин. Принцип двоїстості. Тотожні перетворення формул алгебри множин. | - | |||||
| 2. | Відношення та їх властивості. | - | 7-12 | ||||
| 2.1 | Відношення та операції над ними. Декартів добуток множин. Поняття відношення. Бінарні та n-арні відношення. Область визначення та область значень відношення. Способи задання відношень. Операції над відношеннями. | - | 4-7 | ||||
| 2.2 | Властивості бінарних відношень. Рефлексивність, антирефлексивність, симетричність, антисиметричність, асиметричність, транзитивність, анти-транзитивність відношень. Класи бінарних відношень. Відношення еквівалентності. Класи еквівалентності. Відношення порядку. Відношення толерантності. | - | |||||
| 2.3 | Функціональні відношення. Області визначення і значень. Функції і відображення. Типи відображень: сюр'єкція, ін'єкція, бієкція, | 2,5 | - | 3-5 | |||
| 2.4 | Елементи реляційної алгебри.Реляційна модель даних. Поняття реляційної алгебри. Операції реляційної алгебри. | - | 0,5 | - | |||
3  (сам. роб.) | Алгебри (алгебраїчні структури) | - | - | 1,5 | - | ||
3.1  (сам. роб.) | Алгебраїчні операції та їх властивості. Унарна, бінарна, n-арна операція. Способи записів операцій. Основні властивості операцій. Операції додавання та множення за модулем. | - | - | 0,5 | - | ||
| 3.2 (сам. роб.) | Поняття алгебраїчної структури Підструктура. Морфізми (гомоморфізм, ізоморфізм). Найпростіші алгебраїчні структури. Кільці і поля. Гратки. | - | - | - | |||
| Підсумок | 10-17 | ||||||
| ІІ | Основи математичної логіки | 19-32 | |||||
| 4.1 | Двійкова логіка. Булеві функції та перетворення. | 12,5 | 12-20 | ||||
| 4.1.1 | Булеві функції (основні поняття). Булева алгебра.Булеві змінні і функції. Область визначення та область значень булевий функцій. Способи задання булевих функцій. Реалізація булевих функцій формулами. Елементарні функції алгебри логіки. Двоїстість. Двоїсті та самодвоїсті булеві функції. Принцип двоїстості. Закони і тотожності булевої алгебри. Еквівалентні перетворення формул булевої алгебри. | 3-5 | |||||
| 4.1.2 | Нормальні форми булевих функцій. Основні поняття. Нормальні форми: диз'юнктивна нормальна форма (ДНФ), кон’юнктивна нормальна форма (КНФ). Досконалі нормальні форми (ДДНФ, ДКНФ). Диз’юнктивні та кон’юнктивні розкладання булевих функцій. Перехід від таблиці булевої функції до формули алгебри логіки і навпаки. | 3-5 | |||||
| 4.1.3 | Мінімізація булевих функцій.Основні поняття. Критерії мінімізації. Основні методи мінімізації булевих функцій. Метод мінімізуючих карт (діаграми Карно-Вейча). | 3-5 | |||||
| 4.1.4 | Алгебра Жегалкіна. Структура і тотожністі алгебри Жегалкіна. Поліном Жегалкіна та правило його побудови. Лінійні булеві функції. | 1,5 | 3-5 | ||||
| 4.1.5 | Функціональна повнота наборів булевих функцій. Типи булевих функцій. Замкнені класи булевих функцій. Поняття повноти набору булевих функцій. Теореми Поста про функціональну повноту набору булевих функцій. | 1,5 | |||||
| 4.1.6 (сам. роб.) | Логічні схеми. Синтез комбінаційних схем. Перемикальні ланцюги; двох- і багатоступінчасті комбінаційні схеми. | - | - | 0,5 | |||
| 4.2 | Логіка висловлень. | 3,5 | 3-6 | ||||
| 4.2.1 | Висловлення. Алгебра висловлень. Висловлення (основні поняття). Логічні зв'язки і формули логіки вісловлень. Побудова складних формул. Алгебра логіки і логіка висловлень. Інтерпретація формул логіки висловлень. Правильні міркування. Логічна еквівалентність і логічний наслідок. | 1,5 | 3-6 | ||||
| 4.2.2 | Обчислення висловлень.Аксіоми та повнота обчислення логіки висловлень. Висновки в обчисленні висловлень. Дедуктивні висновки у логіці висловлень. Несуперечність, незалежність. Різні аксіоматизації обчислення висловлень. | ||||||
| 4.3 | Логіка предикатів (Логіка першого порядку). | 3,5 | 4-6 | ||||
| 4.3.1 | Предикати. Алгебра предикатів. Основні поняття логіки предикатів. Операції логіки предикатів. Кванторні операції. Формули та їх інтерпретація у логіці предикатів. Закони і тотожності логіки предикатів. Випереджені нормальні форми. | 4-6 | |||||
| 4.3.2 | Обчислення предикатів. Логічний висновок у логіці предикатів. | 1,5 | |||||
4.4  (сам. роб.) | Багатозначна логіка. Основні поняття і функції k-значної логіки. | - | - | 0,5 | |||
| Основи комбінаторного аналізу | 9,5 | 7-11 | |||||
| 5.1 (сам. роб.) | Історія розвитку комбінаторики. Класичні задачі комбінаторного аналізу. Сучасні задачі, які вирішуються комбінаторними методами. | - | - | 0,5 | |||
| 5.2 | Загальні визначення комбінаторики. Моделі типових комбінаторних конфігурацій. Поняття r-вибірки. Загальні правила і задачі комбінаторики. Правила суми і добутку. Перестановки, розміщення, сполучення (без повторень та з повтореннями). | 3-5 | |||||
| 5.3 (сам. роб.) | Властивості сполучень. Біном Ньютона. Біноміальні коефіцієнти. Трикутник Паскаля. Поліноміальна теорема. | - | 0,5 | ||||
| 5.4 | Принцип включення і виключення. Теорема та формула включень і виключень. | 1,5 | |||||
| 5.5 | Задачі про розподіл предметів за урнами (урнові схеми вирішення комбінаторних задач). Розподіл однакових об’єктів за урнами. Розподіл неоднакових об’єктів за урнами. Числа Стирлинга. Числа Моргана. Числа Белла. Композиції і розбиття. | 4-6 | |||||
| 5.6 | Підходи до вивчення комбінаторних об’єктів і чисел. Поняття про продуктивні функції. Поняття про рекурентні співвідношення. | - | 0,5 | ||||
5.6.1  | Метод продуктивних функцій. Продуктивні функції сполучень. Продуктивні функції розміщень та перестановок. Продуктивні функції для розбиття чисел. | - | - | ||||
| 5.6.2 | Метод рекурентних співвідношень. Числа Фібоначчі. | - | - | 0,5 | |||
| 6(сам. роб.) | Основи теорії кодування.Алфавітне кодування. Кодування з мінімальною надлишковістю. Алгоритм Фано. Алгоритм Хаффмена. Завадостійке кодування. Стиснення даних. Криптографія. | - | - | ||||
| Контрольна робота (позааудиторна) | - | - | 4(КРд) | 3-5 | |||
| Підсумок | 35,5 | 29-48 | |||||
| ІІІ | Основні поняття теорії графів | 31,5 | 2(КРа) | 18-29 | |||
| 7.1 (сам. роб.) | Зародження теорії графів як математичної дисципліни. Типові задачі теорії графів. | - | - | 0,5 | |||
| 7.2 | Походження графів. Визначення графів. Різновиди графів. Неорієнтовані та орієнтовані графи. Основні терміни для неорієнтованих та орієнтованих графів. Способи задання графів. Геометрична реалізація графів. Матриця суміжності. Матриця інциденцій. Число вершин і ребер графа. | 4-6 | |||||
| 7.3 | Операції над графами. Операції вилучення ребер та вершин. Операція введення ребра, операція введення вершини у ребро. Операція об’єднання графів. Операції додавання і множення графів. | 2,5 | |||||
| 7.4 | Ізоморфізм графів. Підграфи. Алгебраїчний критерій ізоморфізму графів. Зв'язок з відношеннями. Ізоморфізм як відношення еквівалентності. Плоскі та планарні графи. Гомеоморфні графи. Теорема Понтрягіна-Куратовського. Теорема Жордана. Жорданова крива. Побудова плоского зображення графа. | 1,5 | 3-5 | ||||
| 7.5 | Зв'язність графів. Ейлерові та гамільтонові графи.Поняття зв'язності графів, компонента зв'язності, n-зв'язний граф. Властивості зв'язних графів. Метричні характеристики зв'язних графів. Ейлерові та гамільтонові графи. Теорема Ейлера. Алгоритм знаходження ейлерова цикла (теорема Флері). Ознаки існування гамільтонових циклів, шляхів і контурів. | ||||||
| 7.6 | Цикломатика графів. Цикломатичне число та його властивості. Цикломатична матриця. Базис циклів. Алгоритм побудови базису циклів. | - | 0,5 | ||||
| 7.7 (сам. роб.) | Задача комівояжера. Приклади практичних задач, що зводяться до задачі комівояжера. | - | - | ||||
| 7.8 | Дерева. Визначення дерева, властивості дерев, ліс. Перелічення графів і дерев. Остови графа. Орієнтовані і бінарні дерева. Правила обходу бінарних дерев. Еквівалентні бінарні дерева. | 3-5 | |||||
| 7.9 | Розфарбування графів. Фарбування вершин та ребер. Хроматичне число, теорема про біхроматичний граф. Хроматичний клас. Теорема Брукса. Гіпотеза чотирьох фарб. Теорема про п'ять фарб. Прикладні задачі, що зв’язані з розфарбуванням графів | - | 0,5 | ||||
| 7.10 | Двудольні та k-дольні графи. | 0,5 | |||||
| 7.11 | Транспортні мережі та течії. Їх властивості. | ||||||
| 7.11.1 | Найкоротші відстані та шляхи у мережах. Алгоритм визначення відстані між вершинами на графі з одиничними довжинами ребер. Алгоритм Дейкстри (Форда) визначення відстані між вершинами на графі з довільними довжинами ребер. | 2,5 | 4-6 | ||||
| 7.11.2 (сам. роб.) | Алгоритми Флойда і Данцига пошуку найкоротших шляхів між всіма парами вершин графа | - | - | ||||
| 7.11.3 | Течії у мережах. Задача про максимальну течію у мережі. Розріз мережі. Теорема про максимальну течію і мінімальний розріз. Алгоритм Форда-Фалкерсона. | 4-7 | |||||
| 8(сам. роб.) | Елементи теорії формальних граматик. Задачі формалізації мов та перекладу. Задання мов за допомогою граматик. Типи граматик. | - | - | ||||
| 9(сам. роб.) | Елементи теорії скінчених автоматів. Загальна характеристика автоматів. Розпізнавачі. Скінченні автомати. Способи задання автоматів. Автомати Мили і Мура. Автомати з магазинною пам’яттю. Машина Тьюринга. | ||||||
| Контрольна робота (аудиторна) | - | - | - | 2(КРа) | 3-6 | ||
| Підсумок | 31,5 | 21-35 | |||||
| Усього за семестр | 60-100 |
4.2 Практичні заняття
| Номер зміст. модулю | Но-мер п/з | Назва розділу або теми | Обсяг, год. | Рей-тингова оцінка | Літературні джерела |
| 1.1, 1.2 | Множини. Алгебра множин. | 3-5 | 1-4, 6-9, 13, 14-16, 19-21 | ||
| 2.1, 2.2 | Відношення та операції над ними. | 4-7 | 1-4, 6-9, 13, 14-16, 19-21 | ||
| 2.3 | Функціональні відношення. | 3-5 | 1-4, 18, 19, 20 | ||
| 4.1.1 | Булеві функції та перетворення. | 3-5 | 1-8, 13-21 | ||
| 4.1.2 | Нормальні форми зображення булевих функцій. | 3-5 | 1-8, 13-21 | ||
| 4.1.3 | Мінімізація булевих функцій. | 3-5 | 1-8, 13-21 | ||
| 4.1.4, 4.1.5 | Функціональна повнота наборів булевих функцій. | 3-5 | 1-7, 14 | ||
| 4.2 | Логіка та обчислення висловлень. | 3-6 | 1-8, 13-21 | ||
| 4.3 | Логіка та обчислення предикатів. | 4-6 | 1-8, 13-21 | ||
| 5.2-5.4 | Основні правила комбінаторики. Моделі комбінаторних конфігурацій. | 3-5 | 1,2,4,6, 7-21 | ||
| 5.5 | Урнові схеми вирішення комбінаторних задач | 4-6 | 1,2,4,6, 7-21 | ||
| 6.1, 6.2 | Способи задання графів. Операції над графами. | 4-6 | 1,2,4,6-8, 11, 16, 19, 21 | ||
| 7.4, 7.5 | Зв'язність графів. Ейлерові та гамільтонові графи. | 3-5 | 1,2,4,6-8, 11, 16, 19, 21 | ||
| 7.8 | Дерева. Алгоритми побудови остовного дерева. | 3-5 | 1,2,4,6-8, 11, 16, 19, 21 | ||
| 7.11.1, 7.11.2 | Відшукання найкоротших відстаней між вершинами графа (мережі) | 4-6 | 1,2,4,6-8, 11, 16, 19, 20 | ||
| 7.11.3 | Задачі про максимальну течію і максимальний розріз у мережі. | 4-7 | 1,2,4,6-8, 11, 16, 19, 20 | ||
| Загальна кількість годин | 54-89 |
4.3. Самостійна робота студента
| Номер зміст. модулю | Форми самостійної роботи | Обсяг, годин | Вид контролю | Літерат. джерела |
| 1,2,4,5,7 | Вивчення лекційного матеріалу | Усн. опит, експрес-контр. | 1-21 | |
| 1,2,4,5,7 | Підготовка до практичних занять | Усн. опит, експрес-контр. | 1-21 | |
| Підготовка до позааудиторної (домашньої) контрольної роботи | Позааудит. КР | 1-7, 14 | ||
| Підготовка до аудиторної контрольної роботи | Ауд. КР | 1,2,4,6-8, 11, 16, 19, 21 | ||
| Теми для самостійного вивчення: | ||||
| 1.2 | Історія зародження, розвитку і становлення дискретної математики. Внесок вчених у її розвиток. | 0,5 | Усн. опит. | 1, 4 |
| 3.1 | Алгебраїчні операції та їх властивості. Унарна, бінарна, n-арна операція. Способи записів операцій. Основні властивості операцій. Операції додавання та множення за модулем. | 0,5 | Усн. опит, експрес-контр., іспит | 1, 4, 19 |
| 3.2 | Поняття алгебраїчної структури Підструктура. Морфізми (гомоморфізм, ізоморфізм). Найпростіші алгебраїчні структури. Кільці і поля. Гратки. | Усн. опит, експрес-контр., іспит | 1, 4, 19 | |
| 4.1.6 | Логічні схеми. Синтез комбінаційних схем. Перемикальні ланцюги; двох- і багатоступінчасті комбінаційні схеми. | 0,5 | Усн. опит, іспит | 1-8, 13-16, 18-19 |
| 4.4 | Багатозначна логіка. Основні поняття і функції k-значної логіки. | 0,5 | Усн.опит., іспит | 1-8, 13-16, 18-19 |
| 5.1 | Історія розвитку комбінаторіки. Класичні задачі комбінаторного аналізу. Сучасні задачі, які вирішуються комбінаторними методами. | 0,5 | Усн. опит, експрес-контр., іспит | 1,2,4,7,9,11, 17, 1-21 |
| 5.3 | Властивості сполучень. Біном Ньютона. Біноміальні коефіцієнти. Трикутник Паскаля. Поліноміальна теорема. | 0,5 | Усн. опит, експрес-контр., іспит | 1, 4, 7, 19 |
| 5.6.1 | Метод продуктивних функцій. Продуктивні функції сполучень. Продуктивні функції розміщень та перестановок. Продуктивні функції для розбиття чисел. | Усн. опит., іспит | 1,2,4,6,7,8,19 | |
| 5.6.2 | Метод рекурентних співвідношень. Числа Фібоначчі. | 0,5 | Усн.опит. | 1,2,4,6,7,8,19 |
| Основи теорії кодування. Алфавітне кодування. Кодування з мінімальною надлишковістю. Алгоритм Фано. Алгоритм Хаффмена. Завадостійке кодування. Стиснення даних. Криптографія. | Усн. опит., іспит | |||
| 7.1 | Зародження теорії графів як математичної дисципліни. Типові задачі теорії графів. | 0,5 | Усн. опит., іспит | 1,2,4,6-8, 11, 16, 19, 20, 21 |
| 7.7 | Задача комівояжера. Приклади практичних задач, що зводяться до задачі комівояжера. | Усн. опит, експрес-контр. | 1,2,4,6-8, 11, 16, 19, 20 | |
| 7.11.2 | Алгоритми Флойда і Данцига пошуку найкоротших шляхів між всіма парами вершин графа | Усн.опит, експрес-контр., іспит | 1,2,4,6-8, 11, 16, 19, 20 | |
| Елементи теорії формальних граматик. Задачі формалізації мов та перекладу. Задання мов за допомогою граматик. Типи граматик. | Усн. опит., іспит | |||
| Елементи теорії скінчених автоматів. Загальна характеристика автоматів. Розпізнавачі. Скінченні автомати. Способи задання автоматів. Автомати Мили і Мура. Автомати з магазинною пам’яттю. Машина Тьюринга. | Усн. опит., іспит | 1, 4, 7 | ||
| Усього годин |
4.4. Рейтингова оцінка за дисципліною
4.4.1 Кількісні критерії оцінювання
Як форма підсумкового контролю для дисципліни «Дискретна математика» використовується комбінований іспит.
Рейтингова оцінка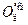 
з дисципліни «Дискретна математика» має дві складові: 
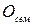– кількість балів, отриманих студентом протягом семестру (максимальна рейтингова оцінка протягом семестру – 100 балів) та 
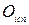– кількість балів, отриманих студентом на іспиті (максимальний бал також становить 100) і формується у такий спосіб:
.
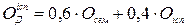При формуванні оцінок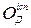 
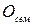, та 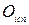округлювання проводиться до цілого за правилами математики.
Для оцінювання роботи студента протягом семестру рейтингова оцінка 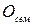є накопичувальною та розраховується як сума оцінок за різні види занять (робіт): за лекційні заняття; за практичні заняття (ПЗ); за самостійну роботу (СР), за аудиторну контрольну роботу (КРа), за позааудиторну (домашню) контрольну роботу (КРд). Знання матеріалу лекційних занять і самостійної роботи оцінюється на практичних заняттях у вигляді оцінювання відповіді на контрольні запитання, які надаються в методичних вказівках до практичних занять з дисципліни, усних та письмових відповідей на запитання (експрес-опитування). Оцінювання цього матеріалу здійснюється при відпрацюванні практичних занять.
Практичні заняття з урахуванням лекційного матеріалу і матеріалів самостійної роботи, контрольні роботи оцінюються за 100-бальною системою. Кількість балів за кожне практичне заняття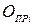 
складається з балів 
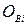, якими оцінюється присутність і відпрацювання практичних занять, а також з балів 
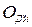, якими оцінюється виконання домашніх завдань з кожного практичного заняття, тобто 
.
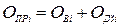Оцінка за кожне практичне заняття 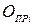, оцінки за аудиторну контрольну роботу ( 
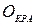) та позааудиторну (домашню) контрольну роботу 
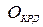наведені в таблиці «Рейтингова оцінка за дисципліною».
Таблиця «Рейтингова оцінка за дисципліною»
| Вид заняття / контрольний захід | Оцінка | Оцінка за присутність і відпрацювання ПЗ | Оцінка виконання домашніх завдань з кожного ПЗ |
| Практичне заняття №1 | |||
| Практичне заняття №2 | |||
| Практичне заняття №3 | |||
| Контрольна точка 1 | |||
| Практичне заняття №4 | |||
| Практичне заняття №5 | |||
| Практичне заняття №6 | |||
| Практичне заняття №7 | |||
| Практичне заняття №8 | |||
| Практичне заняття №9 | |||
| Практичне заняття №10 | |||
| Практичне заняття №11 | |||
| Контрольна робота (КРд) (позааудиторна) | - | - | |
| Контрольна точка 2 | |||
| Практичне заняття №12 | |||
| Практичне заняття №13 | |||
| Практичне заняття №14 | |||
| Практичне заняття №15 | |||
| Практичне заняття №16 | |||
| Контрольна робота (КРа) (аудиторна) | - | - | |
| Контрольна точка 3 | |||
| Усього за семестр |
При цьому виді контролю підсумкова оцінка 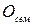(у 100-бальній системі) обчислюється за формулою 
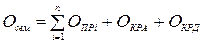, де 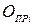– оцінка за кожне практичне заняття; 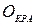– оцінка за аудиторну контрольну роботу, 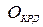– оцінка за позааудиторну (домашню) контрольну роботу.
Комбінований іспит передбачає поєднання таких видів роботи як письмову відповідь на екзаменаційний білет та усну відповідь. Білет для комбінованого іспиту складається з двох теоретичних запитань та двох практичних завдань. Теоретичні запитання оцінюються за 100-бальною шкалою у 25 балів кожне і практичні завдання – в 25 балів кожне. Питання з самостійної роботи над дисципліною (опрацювання матеріалу додаткової літератури тощо) введені в теоретичну частину іспиту у вигляді теоретичних запитань.
Рейтингова оцінка в діапазоні [60-100] вважається позитивною, а в діапазоні [1-59] – незадовільною і підлягає перездачі.
4.4.2 Якісні критерії оцінювання
4.4.2.1 Необхідний обсяг знань для одержання позитивної оцінки.
1. Основні поняття теорії множин. Способи задання множин. Підмножини. Булеан множини. Геометрична інтерпретація множин: кола Алгебра множин. Операції на множинах. Формули і тотожності алгебри множин. Тотожні перетворення виразів.
2. Відношення та їх властивості. Поняття відношення. Способи задання відношень. Операції над відношеннями. Властивості бінарних відношень. Класи бінарних відношень. Функціональні відношення. Реляційна модель даних. Операції реляційної алгебри.
3. Алгебраїчні структури. Алгебраїчні операції та їх властивості. Способи записів операцій. Поняття алгебраїчної структури. Ізоморфізм, гомоморфізм. Найпростіші алгебраїчні структури.
4. Двійкова логіка. Булеві функції та перетворення. Способи задання булевих функцій. Закони і тотожності алгебри логіки. Еквівалентні перетворення формул алгебри логіки. Двоїстість. Нормальні форми булевих функцій. Алгебра Жегалкіна. Функціональна повнота наборів булевих функцій. Методи мінімізації булевих функцій. Логічні схеми. Синтез комбінаційних схем.
5. Логіка висловлень. Поняття атома, молекули, формули. Логічні зв'язки. Побудова складних формул. Інтерпретація формул у логіці висловлень. Дедуктивні висновки у логіці висловлень. Обчислення висловлень.
6. Логіка предикатів (Логіка першого порядку). Основні поняття логіки предикатів. Формули у логіці предикатів. Закони і тотожності у логіці предикатів. Квантори. Випереджені нормальні форми. Логічніий висновок у логіці предикатів. Обчислення предикатів.
7. Основи комбінаторного аналізу. Моделі комбінаторних конфігурацій. Правила суми і добутку. Перестановки, розміщення і сполучення без повторень та з повтореннями. Біном Ньютона. Задачі про розподіл предметів за урнами (урнові схеми вирішення комбінаторних задач). Композиції і розбиття. Метод продуктивних функцій. Метод рекурентних співвідношень. Числа Фібоначчі. Теорема та формула включень і виключень.
8. Основи теорії кодування. Алфавітне кодування. Кодування з мінімальною надлишковістю. Алгоритм Фано. Алгоритм Хаффмена. Завадостійке кодування. Стиснення даних. Криптографія.
9. Основні поняття теорії графів. Визначення графів. Різновиди графів. Способи задання графів. Геометрична реалізація графів. Операції над графами. Ізоморфізм графів. Плоскі та планарні графи. Зв'язність графів. Метричні характеристики зв'язних графів. Ейлерові і гамільтонові графи. Цикломатика графів. Задача комівояжера. Визначення дерева, властивості дерев, ліс. Розфарбування графів. Транспортні мережі та течії.
10. Елементи теорії формальних граматик. Задачі формалізації мов та перекладу. Задання мов за допомогою граматик. Типи граматик.
11. Елементи теорії скінчених автоматів. Загальна характеристика автоматів. Розпізнавачі. Скінченні автомати. Способи задання автоматів. Автомати Мили і Мура. Автомати з магазинною пам’яттю. Машина Тьюринга.
4.4.2.2 Необхідний обсяг умінь для одержання позитивної оцінки.
1. Уміти аналізувати логічну та алгоритмічну структуру фізичних та технологічних процесів, процесів обробки інформації в природі та суспільстві. Уміти використовувати апарат дискретної математики для формалізації та математичного опису задач, що виникають у сфері науки та виробництва.
2. Уміти виконувати аналіз та синтез дискретних об’єктів та процесів, використовуючи поняття і закони теорії множин.
3. Уміти реалізувати у математичних термінах на абстрактних множинах реальні зв’язки між реальними об’єктами з використанням операцій, які визначені для відношень. Уміти використовувати елементи теорії відношень для формування та аналізу таких структур даних, як списки, дерева тощо.
4. Уміти використовувати елементи теорії реляційної алгебри для побудови комп’ютерних баз даних.
5. Уміти вирішувати комбінаторні задачі на перелічення, задачі про існування та побудову, задачі про вибір об’єктів.
6. Уміти моделювати та аналізувати за допомогою теорії графів будь-які схеми, в яких виділяються більш прості частини (вершини) і зв’язки між ними (ребра). Уміти вирішувати задачі відшукання найкоротших відстаней між вершинами графа (мережі), задачі відшукання оптимальних структур об’єктів.
7. Уміти виконувати аналіз та синтез дискретних об’єктів та процесів, використовуючи елементи булевої алгебри (формувати булеві функції, їх нормальні форми). Уміти проводити мінімізацію булевих функцій.
8. Уміти за допомогою елементів алгебри логіки (алгебри висловлень, алгебри предикатів) описувати міркування та «обчислювати» їх результати.
4.4.2.3 Критерії оцінювання роботи студента протягом семестру.
Задовільно, D, E (60-74). Оцінку «задовільно» заслуговує студент, який виявив мінімум знання основного змісту матеріалу з дисципліни в об’ємі, необхідному для подальшого навчання й майбутньої роботи за напрямом (спеціальністю), який справився з виконанням усіх практичних занять (робіт), що передбачені програмою, але у звітах (результатах домашніх і аудиторних робіт) і відповіді на запитання є похибки.
Добре, С (75-89). Оцінку «добре» заслуговує студент, який виконав усі домашні завдання, відпрацював всі практичні заняття, виконав контрольні роботи, який виявив повне знання програмного матеріалу, вірно розкрив суть проблем та у цілому розв’язав завдання практичних занять, але у змісті відповіді є незначні помилки, або недостатньо обґрунтовано надані відповіді на запропоновані запитання з лекційного матеріалу з дисципліни, з матеріалу практичних занять та матеріалу з самостійної роботи.
Відмінно, А, В (90-100). Оцінку «відмінно» заслуговує студент, який виявив всебічні чіткі, систематичні та глибокі знання теоретичного та практичного навчального матеріалу з дисципліни, вірно розкрив суть і достатньо обґрунтував своє ставлення до запропонованих питань, виявив вміння вільно виконувати практичні завдання, що передбачені програмою, а також безпомилково виконав вправи, вміє аналізувати і систематизувати інформацію.
5. НАВЧАЛЬНО-МЕТОДИЧНІ МАТЕРІАЛИ З ДИСЦИПЛІНИ
Дисципліна вивчається з 2008 р.
5.1. Основна література
1. Бондаренко, М. Ф. Комп’ютерна дискретна математика [Текст] : підручник / М. Ф. Бондаренко, Н. В. Білоус, А. Г. Руткас. – Харків: «Компанія СМІТ», 2004. – 480 с. (існує електронний варіант).
2. Капітонова, Ю. В. Основи дискретної математики [Текст] / Ю. В. Капітонова, С. Л. Кривий, О. А. Летичевський, Г. М. Луцький, М. К. Печорін – Київ: Наукова думка, 2002. – 578 с.
3. Тевяшев, А. Д. Основы дискретной математики в примерах и задачах [Текст] : учеб. пособие для вузов / А. Д. Тевяшев, И. Г. Гусарова. – Харьков: ХНУРЭ, 2003. – 272 с.
4. Бардачев, Ю. Н. Основы дискретной математики [Текст] : учебное пособие / Ю. Н. Бардачев, Н. А. Соколова, В. Е. Ходаков; под редакцией В. Е. Ходакова. – Херсон: ХГТУ, 2000. – 356 с. (існує електронний варіант).
5. Шапорев, С. Д. Дискретная математика. Курс лекций и практических занятий [Текст] / С. Д. Шапорев – СПб.: БХВ-Петербург, 2006. – 400 с. (існує електронний варіант).
6. Кузнецов, О. П. Дискретная математика для инженера [Текст] / О. П. Кузнецов, Г. М. Адельсон-Вельский. – М.: Энергоатомиздат, 1988. – 480 с.
7. Сигорский, В. П. Математический аппарат инженера [Текст] / В. П. Сигорский. – Киев: Техніка, 1977. – 768 с. (існує електронний варіант).
8. Яблонский, С. В. Введение в дискретную математику [Текст] / С. В. Яблонский. – М.: Наука, 1986. – 384 с.
9. Горбатов, В.А. Основы дискретной математики [Текст] / В. А. Горбатов – М.: Высшая школа, 1986. – 312с.
10. Харари, Ф. Теория графов [Текст] / Ф. Харари. – М.: Мир, 1973. – 304 с.
11. Глускин, Л.М. Задачи и алгоритмы комбинаторики и теории графов [Текст] / Л. М. Глускин, В. Я. Шварц, Л. А. Шор. – Донецк: Изд-во ДПИ, 1982. – 110с.
12. Білоус, Н.В. Основи комбінаторного аналізу. [Текст] : навч. посібник / Н. В. Білоус, З. В. Дудар, Н. С. Лєсна, І. Ю. Шубін. – Харків: ХТУРЕ, 1999. – 96 с.
13. Бондаренко, М. Ф. Збірник тестових завдань з дискретної математики [Текст] / М. Ф. Бондаренко, Н. В. Білоус, І. Ю. Шубін. – Харків: ХТУРЕ, 2000. – 156 с. (існує електронний варіант).
5.2. Додаткова література
14. Новиков, Ф. А. Дискретная математика для программистов [Текст] / Ф. А. Новиков. – СПб: Питер, 2001. – 304 с. (існує електронний варіант).
15. Донской, В.И. Дискретная математика [Текст] / В. И. Донской. – Симферополь: СОНАТ, 2000. – 360 с.
16. Андерсон, Дж. А. Дискретная математика и комбинаторика [Текст] / Джеймс А. Андерсон. – М.: Издательский дом «Вильямс», 2003. – 960 с.
17. Виленкин, Н.Я. Комбинаторика [Текст] / Н. Я. Виленкин. – М.: Наука, 1969. – 328 с.
18. Белоус, Н.В. Тесты. Физика. Математическая логика [Текст] : Навч. посібник / Н. В. Белоус, Е. Е. Гетьманова, З. В. Дударь, В. Ф. Захарченко, М. А. Красноголовец, Н. С. Лесная, В. В. Семенец, В. А. Стороженко, А. А. Харьковская. – Харків: ХТУРЕ, 1998. – 152 с.
19. Капитонова, Ю. В. Лекции по дискретной математике [Текст] / Ю. В. Капитонова, С. Л. Кривой, А. А. Летичевский, Г. М. Луцкий. – СПб.: БХВ-Петербург, 2004. – 624 с.
5.3. Методичні посібники та вказівки
20. Методичні вказівки до практичних робіт з дисципліни «Дискретна математика» / Упоряд. Н. В. Васильцова. – Харків: ХНУРЕ, 2007. ( електронний варіант).
21. Методичні вказівки до практичних занять і самостійної роботи з курсу «Основи дискретної математики» [Текст] / Захарченко В. Ф., Дедіков Е. О. – Харків, ХТУРЕ, 2002. – 44 с.
6. ПИТАННЯ ОХОРОНИ ПРАЦІ ПРИ ВИВЧЕННІ ДИСЦИПЛІНИ
1. Проведення інструктажів з охорони праці та безпеки життєдіяльності на початку роботи з групами студентів. Розглядання питань щодо правових, соціально-економічних, організаційно-технічних, санітарно-гігієнічних заходів з охорони праці студентів у процесі навчання у вищому навчальному закладі.
Доповнення та зміни у робочій програмі
Перелік деталізованих компетенцій
| Шифр компетенції | Шифр деталізованої компетенції | Найменування деталізованої компетенції |
| КЗН.02 | КЗН.02.01 | Базові знання в області дискретної математики, їх місце в системі підготовки фахівців з комп'ютерних наук, уміння застосовувати ці знання в науково-дослідній і професійній діяльності |
| КЗН.02.02 | Базові знання в області теорії множин та уміння їх застосовувати в науково-дослідній і професійній діяльності | |
| КЗН.02.03 | Базові знання в області теоретичних основ булевої алгебри та уміння їх застосовувати в науково-дослідній і професійній діяльності | |
| КЗН.02.04 | Базові знання в області алгебри Жегалкіна та уміння їх застосовувати в науково-дослідній і професійній діяльності | |
| КЗН.02.05 | Базові знання в області теорії і алгебри висловлень та уміння їх застосовувати в науково-дослідній і професійній діяльності | |
| КЗН.02.06 | Базові знання в області алгебри предикатів та уміння їх застосовувати в науково-дослідній і професійній діяльності | |
| КЗН.02.07 | Базові знання в області комбінаторного анлізу та уміння їх застосовувати в науково-дослідній і професійній діяльності | |
| КЗН.02.08 | Базові знання в області теорії графів та уміння їх застосовувати в науково-дослідній і професійній діяльності | |
| КЗН.02.09 | Базові знання в області прикладних аспектів теорії графів-дерев та уміння їх застосовувати в науково-дослідній і професійній діяльності | |
| КЗН.02.10 | Базові знання в області розфарбування графів та уміння їх застосовувати в науково-дослідній і професійній діяльності | |
| КІ.03 | КІ.03.01 | Здатність аналізувати та синтезувати науково-технічну, природничо-наукову інформацію за допомогою загальної теорії відношень |
| КІ.03.02 | Здатність аналізувати та синтезувати науково-технічну, природничо-наукову інформацію у вигляді функціональних відношень | |
| КІ.03.03 | Здатність аналізувати та синтезувати двійкову інформацію у вигляді нормальних форм булевих функцій | |
| КІ.03.04 | Здатність аналізувати, мінімізувати двійкову інформацію, яка подається у вигляді булевих функцій | |
| КІ.03.05 | Здатність аналізувати функціональну повноту наборів булевих функцій. | |
| КІ.03.06 | Здатність аналізувати та синтезувати інформацію, що надається у вигляді комбінаторних об’єктів і чисел. | |
| КІ.03.07 | Здатність аналізувати інформацію, яка надається у вигляді ізоморфних графів | |
| КІ.03.08 | Здатність аналізувати інформацію, яка надається у вигляді ейлерових та гамільтонових графів | |
| КІ.03.09 | Здатність аналізувати та синтезувати інформацію з цикломатики графів | |
| КЗП.01 | КЗП.01.01 | Ґрунтовна математична підготовка, а також підготовка з теоретичних, методичних і алгоритмічних основ інформаційних технологій для використання математичного апарату реляційної алгебри під час вирішення прикладних і наукових завдань в області розробки і використання баз даних інформаційних систем |
| КЗП.01.02 | Підготовка з теоретичних, методичних і алгоритмічних основ інформаційних технологій для використання математичного апарату комбінаторного аналізу (принципів включення і виключення) під час вирішення прикладних і наукових завдань в області інформаційних систем і технологій | |
| КЗП.01.03 | Ґрунтовна математична підготовка, а також підготовка з теоретичних, методичних і алгоритмічних основ інформаційних технологій для використання математичного апарату пошуку найкоротших відстаней та шляхів у мережах під час вирішення прикладних і наукових завдань в області інформаційних систем і технологій | |
| КЗП.01.04 | Ґрунтовна математична підготовка, а також підготовка з теоретичних, методичних і алгоритмічних основ інформаційних технологій для використання математичного апарату пошуку течій у мережах під час вирішення прикладних і наукових завдань в області інформаційних систем і технологій | |
| КСП.02 | КСП.02.01 | Знання дискретних структур для вирішення комбінаторних задач за урновими схемами |
| КСП.02.02 | Вміння застосовувати сучасні методи теорії множин під час аналізу, синтезу та проектуванні інформаційних систем різної природи | |
| КСП.02.03 | Вміння застосовувати сучасні методи теорії відношень під час аналізу, синтезу та проектуванні інформаційних систем різної природи | |
| КСП.02.04 | Вміння застосовувати сучасні методи теорії функціональних відношень під час аналізу, синтезу та проектуванні інформаційних систем різної природи | |
| КСП.02.05 | Вміння застосовувати сучасні методи побудови булевих функцій під час аналізу, синтезу та проектуванні інформаційних систем різної природи | |
| КСП.02.06 | Вміння застосовувати сучасні методи зображення і побудови нормальних форм булевих функцій під час аналізу, синтезу та проектуванні інформаційних систем різної природи | |
| КСП.02.07 | Вміння застосовувати сучасні методи мінімізації булевих функцій під час аналізу, синтезу та проектуванні інформаційних систем різної природи | |
| КСП.02.08 | Вміння застосовувати сучасні методи пошуку функціональної повноти булевих функції під час аналізу, синтезу та проектуванні інформаційних систем різної природи | |
| КСП.02.09 | Вміння застосовувати сучасні методи логіки та обчислення висловлень під час аналізу, синтезу та проектуванні інформаційних систем різної природи | |
| КСП.02.10 | Вміння застосовувати сучасні методи логіки та обчислення предикатів під час аналізу, синтезу та проектуванні інформаційних систем різної природи | |
| КСП.02.11 | Вміння застосовувати сучасні методи побудови моделей комбінаторних конфігурацій під час аналізу, синтезу та проектуванні інформаційних систем різної природи | |
| КСП.02.12 | Вміння застосовувати урнові схеми вирішення комбінаторних задач під час аналізу, синтезу та проектуванні інформаційних систем різної природи | |
| КСП.02.13 | Вміння застосовувати сучасні методи задання графів та операцій над ними під час аналізу, синтезу та проектуванні інформаційних систем різної природи | |
| КСП.02.14 | Вміння застосовувати ейлерові та гамільтонові графи під час аналізу, синтезу та проектуванні інформаційних систем різної природи | |
| КСП.02.15 | Вміння застосовувати алгоритми побудови дерев під час аналізу, синтезу та проектуванні інформаційних систем різної природи | |
| КСП.02.16 | Вміння застосовувати сучасні методи відшукання найкоротших відстаней між вершинами графа під час аналізу, синтезу та проектуванні інформаційних систем різної природи | |
| КСП.02.17 | Вміння застосовувати сучасні методи вирішення задач про течії у мережах під час аналізу, синтезу та проектуванні інформаційних систем різної природи |
Доповнення до робочої програми
підготував______________________________________________
(підпис, посаду, прізвище, ініціали)
"Узгоджено"
Зав. кафедрою
______________________ В.М. Левикін
(підпис, прізвище, ініціали)