Формулы Алгебры логики. Суперпозиция булевых функций
Определение. Суперпозицией булевых функций f1, …, fn называется функция f, полученная с помощью подстановок этих функций друг в друга и переименованием переменных. Выражение, описывающее эту суперпозицию называется формулой алгебры логики.
(Лекция 8)
Если функция f соответствует формуле A, то говорят, что формула А реализует функцию f.
Определение. Формулы А и В называются эквивалентными (A ~ B), если соответствующие им функции эквивалентны: f = g (f ~ A, g ~ B).
Пусть f1(x) = 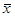 , f2(x, y) = x & y, f3(x, y) = x Ú y, f4(x, y) = x ® y.
, f2(x, y) = x & y, f3(x, y) = x Ú y, f4(x, y) = x ® y.
f(x, y, z) = f3(f2(x, z), f1(f4(y, z)) – суперпозиция
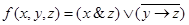 - формула Алгебры логики
- формула Алгебры логики
| Таблица: | x | y | z | x & z | 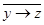 | 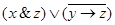 |
Свойства элементарных булевых функций (Законы алгебры логики)
1. Коммутативность:
x & y = y & x x / y = y / x
x Ú y = y Ú x x ¯ y = y ¯ x
x Å y = y Å x x ® y ¹ y ® x
x ~ y = y ~ x
2. Ассоциативность:
x & (y & z) = (x & y) & z x ® (y ® z) ¹ (x ® y) ® z
x Ú (y Ú z) = (x Ú y) Ú z x / (y / z) ¹ (x / y) / z
x Å (y Å z) = (x Å y) Å z x ¯ (y ¯ z) ¹ (x ¯ y) ¯ z
x ~ (y ~ z) = (x ~ y) ~ z
3. Дистрибьютивность:
x & (y Ú z) = (x & y) Ú (x & z) (Дистрибьютивность конъюнкции относительно дизъюнкции)
x Ú (y & z) = (x Ú y) & (x Ú z) (Дистрибьютивность конъюнкции относительно дизъюнкции)
(x Å y) & z = (x & y) Å (x & z)
(x & y) Å z ¹ (x Å y) & (x Å z)
4. Двойное отрицание: 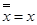
5. Законы де Моргана:
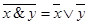
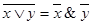
6. x & x = x x Ú x = x 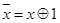 x Å x = 0 x ~ x = 1 x ® x = 1
x Å x = 0 x ~ x = 1 x ® x = 1
x &  = 0 x Ú
= 0 x Ú  = 1 x Å
= 1 x Å  = 1 x ~
= 1 x ~  = 0 x ®
= 0 x ®  =
= 
x & 0 = 0 x Ú 0 = x x Å 0 = x x ~ 0 =  x ® 0 =
x ® 0 = 
x & 1 = x x Ú 1 = 1 x Å 1 =  x ~ 1 = x x ® 1 = 1
x ~ 1 = x x ® 1 = 1
0 ® x = 1
1 ® x = x
7. Выражение эквивалентности другие операции:
x ~ y = 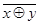 = x Å y Å 1
= x Å y Å 1
x ~ y = (  Ú y) & (x Ú
Ú y) & (x Ú 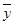 )
)
x ~ y = (x & y) Ú (  &
& 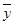 )
)
8. Выражение суммы по модулю 2 через другие операции:
x Å y = (x & 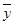 ) Ú (
) Ú (  & y)
& y)
9. Выражение импликации через другие операции:
x ® y = 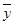 ®
®  x ® y = x & y Å x Å 1
x ® y = x & y Å x Å 1
x ® 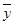 = y ®
= y ®  x ® y =
x ® y =  Ú y
Ú y
x ® y = 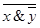
10. x ® (y & z) = (x ® y) & (x ® z)
(x & y) ® z = x ® (y ® z)
x Ú y = (x ® y) ® y
11. Законы поглощения:
x & (x Ú y) = x
x Ú (x & y) = x
Доказательство: 1) x Ú (x & y) = (x & 1) Ú (x & y) = x & (1 Ú y) = x & 1 = x.
2) x & (x Ú y) = (x & x) Ú (x & y) = x Ú (x & y) = [по пункту 1] = x.
Порядок действий в формулах алгебры логики
Если в выражениях нет скобок, то очередность выполнения логических операций следующая:
1) «отрицание»;
2) «конъюнкция»;
3) «дизъюнкция»;
4) «сумма по модулю 2» и «эквивалентность»;
5) «логическое следование».
Пример: 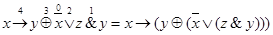
С помощью законов алгебры логики можно упрощать исходные формулы и получать новые.
Существует еще один способ для получения тождеств алгебры логики. Он основан на использовании принципа двойственности.
