Экспоненциальное сглаживание

Предположим, что исследуется временной ряд x_t.

Выявление и анализ тенденции динамического ряда часто производится с помощью его выравнивания или сглаживания. Экспоненциальное сглаживание — один из простейших и распространенных приемов выравнивания ряда. В его основе лежит расчет экспоненциальных средних.

Экспоненциальное сглаживание ряда осуществляется по рекуррентной формуле

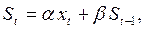(3.7)

где S_t — значение экспоненциальной средней в момент t;

α — параметр сглаживания, α=const, 0 < α < 1;

β = 1 — α.

Выражение (3.7) можно переписать следующим образом:

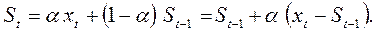(3.8)

Экспоненциальная средняя на момент t здесь выражена как экспоненциальная средняя предшествующего момента плюс доля α разницы текущего наблюдения и экспоненциальной средней прошлого момента.

Если последовательно использовать рекуррентное соотношение (3.7), то экспоненциальную среднюю S_t можно выразить через значения временного ряда х:

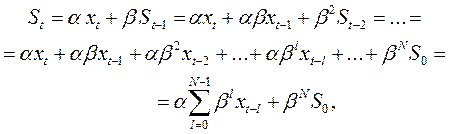(3.9)

где N — количество членов ряда;

S_o — некоторая величина, характеризующая начальные условия для первого применения формулы (3.7) при t = 1.

Так как β < 1, то при 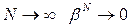, а сумма коэффициентов 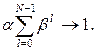Тогда .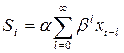

Таким образом, величина S_t оказывается взвешенной суммой всех членов ряда. Причем веса падают экспоненциально в зависимости от давности («возраста») наблюдения. Это и объясняет, почему величина S_t названа экспоненциальной средней.

Рассмотрим, ряд, генерированный моделью

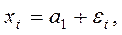
где a₁ — const;

ε_t — случайные неавтокоррелированные отклонения, или шум, со средним значением 0 и дисперсией σ².

Применим к нему процедуру экспоненциального сглаживания (3.7). Тогда

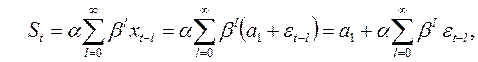
Найдем математическое ожидание

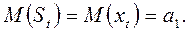
и дисперсию

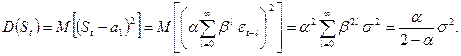(3.10)

Так как 0 < α < 1, D(S_t) < D (x_t)=σ².

Таким образом, экспоненциальная средняя S_t имеет то же математическое ожидание, что и ряд х, но меньшую дисперсию. Как видно из (3.10), при высоком значении α дисперсия экспоненциальной средней незначительно отличается от дисперсии ряда х. Чем меньше α, тем в большей степени сокращается дисперсия экспоненциальной средней.

Следовательно, экспоненциальное сглаживание можно представить как фильтр, на вход которого в виде потока последовательно поступают члены исходного ряда, а на выходе формируются текущие значения экспоненциальной средней.

И чем меньше α, тем в большей степени фильтруются, подавляются колебания исходного ряда.

После появления работ Р. Брауна экспоненциальная средняя часто используется для краткосрочного прогнозирования. В этом случае предполагается, что ряд генерируется моделью

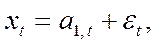
где . a_1,t — варьирующий во времени средний уровень ряда;

ε_t — случайные неавтокоррелированные отклонения с нулевым математическим ожиданием и дисперсией σ².

Прогнозная модель имеет вид

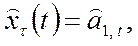
где 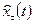— прогноз, сделанный в момент t на τ единиц времени (шагов) вперед;

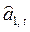— оценка a_1,t (знак ^ над величиной здесь и далее будет означать оценку).

Средством оценки единственного параметра модели служит экспоненциальная средняя 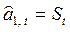. Таким образом, все свойства экспоненциальной средней распространяются на прогнозную модель. В частности, если S_t-1 рассматривать как прогноз на 1 шаг вперед, то в выражении (2) величина (x_t — S_t-1) есть погрешность этого прогноза, а новый прогноз S_t получается в результате корректировки предыдущего прогноза с учетом его ошибки. В этом и состоит существо адаптации.

При краткосрочном прогнозировании желательно как можно быстрее отразить изменения а_1,t и в то же время как можно лучше «очистить» ряд от случайных колебаний.

Таким образом, с одной стороны, следует увеличивать вес более свежих наблюдений, что может быть достигнуто повышением α (см. (3.9)), с другой стороны, для сглаживания случайных отклонений величину α нужно уменьшить.

Эти два требования находятся в противоречии. Поиск компромиссного значения αсоставляет задачу оптимизации модели.

Экспоненциальное выравнивание всегда требует предыдущего значения экспоненциальной средней. Когда процесс только начинается, должна быть некоторая величина S₀, которая может быть использована в качестве значения, предшествующего S₁. Если есть прошлые данные к моменту начала выравнивания, то в качестве начального значения S_o можно использовать арифметическую среднюю всех имеющихся точек или какой-то их части. Когда для такого оценивания S_o нет данных, требуется предсказание начального уровня ряда.

Предсказание может быть сделано исходя из априорных знаний о процессе или на основе его аналогии с другими процессами. После k шагов вес, придаваемый начальному значению, равен (1 — α)^k. Если есть уверенность в справедливости начального значения S_o, то можно коэффициент αвзять малым. Если такой уверенности нет, то параметру α следует дать большое значение, с таким расчетом, чтобы влияние начального значения быстро уменьшилось. Однако большое значение α, как это следует из (3.10), может явиться причиной большой дисперсии колебаний S_t. Если требуется подавление этих колебаний, то после достаточного удаления от начального момента времени величину α можно убавить.