Глава 3. некорректность в обратных задачах геофизики

3.1. Условия корректностив геофизических задачах.

В символическом виде обратная задачагеофизики записывается в виде:

(3.1)

где М - модель изучаемой среды, включающая в себя ее параметризацию; у - заданное физическое поле – результат обработки (возможно тривиальной) наблюдаемой 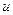; А- оператор прямой задачи – соответствующее уравнение математической физики, определяющее отображение параметров модели среды в параметры физического поля; х - искомый элемент из класса моделей: 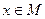. Именно в такой форме записывались рассмотренные в предыдущем разделе конкретные задачи геофизики. В форме (1) записывались как задачи, в которых элементы рассматривались как некоторые функции – элементы функциональных пространств, так и ситуации, в которых - элементы, характеризующиеся конечным числом параметров, а операторы представляют собой некоторые матрицы. Оператор имеет некоторую естественную область определения 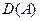, которую можно рассматривать как соответствующее функциональное пространство, а модель является сужением этой области определения. Отвлекаясь пока что от весьма существенного для приложений вопроса о принципах выбора множества М, оператор А будем рассматривать действующим из функционального пространства Х в функциональное пространство Y. Это означает, что Пространства Х и Y могут быть произвольными метрическими пространствами, но в приложениях чаще всего достаточно Гильбертовых с квадратичной нормой.

Задача:

(3.2)

называется расширением задачи (1) или, иначе расширенной обратной задачей. Соответственно (1) это сужение (2) на множество М и, может быть записана в форме:

(3.2-a)

Для одной и той же задачи (1) может быть построено бесконечно много возможных расширений, но, как правило, вид их предопределен физическим смыслом задачи.

Приведем пример расширения обратной задачи.

Предположим, что решается вопрос об изучении распределения горизонтальных плотностных неоднородностей в пласте по выделенному от него аномальному гравитационному полю (для простоты рассмотрим двумерный случай) (рис.1). Пусть пласт разделен вертикальными прямыми на

совокупность из N блоков. Плотность в каждом из них является искомой. Пусть - область i – ого блока. Пусть гравитационное действие в точке x_j i-ого блока, имеющего единичную плотность:

Пусть далее наблюдаемая ) задана в точках х₁, х₂,…х_k. Тогда задача реконструкции значений плотности в ячейках сетки записывается так:

(3.3)

или в матричной форме:

(3.4)

здесь: А – матрица, элементы которой , – вектор искомых параметров модели, представляющих собой значения плотностей в выделенных блоках; - вектор наблюдаемых величин. Если V- область, занимаемая изучаемым пластом ( ), то задача реконструкции горизонтально неоднородной среды может быть в более общей форме сформулирована еще и следующим способом. Пусть - функция плотности, зависящая только от горизонтальных координат. Множество всех таких функций в V образуетподпространство в пространстве всех квадратично интегрируемых в V функций . Связь между распределением плотности из и соответствующей ему вертикальной производной гравитационного потенциала задана соотношением, следующим из (2.2-а):

(3..5)

Если , то [3], и в качестве пространства Y можно принять . Задача (5), где в качестве Х выбрано , а в качестве Y- , есть расширение задачи (3). Формально иным будет расширение, если в качестве Y принять С(Е₀), а в качестве Х . Однако это формальное расширение, не влекущее за собой каких либо конструктивных результатов. Конструктивное расширение задачи (5) и, тем более (3) может быть получено следующим образом.

Рассмотрим в качестве Х- совокупность всех квадратично интегрируемых в V функций σ(x,z). Тогда расширением (5) (и тем более (3)) будет задача реконструкции плотностного распределения:

(3.6)

Последнее расширение особенно интересно в связи с тем, что в отличие от задачи (5), имеющей единственное решение, (6) уже такового не имеет. Решение если есть, то оно не единственно - их бесконечно много. Это весьма характерное для обратных геофизических задач обстоятельство. Оно состоит в том, что чаще всего обратные задачи геофизики допускают некоторое очевидное расширение, в котором решение не единственно. Более того, это расширение вполне естественно и, сужение до задач с единственным решением ассоциируется с некоторым искусственным, натянутым приемом. Но самое важное, состоит в том, что сам факт его существования оказывает влияние на все аспекты, как теории, так и конструирования схем решения суженных задач. Задача (6) это одно из естественных расширений задачи (3) и у него совершенно иные фундаментальные свойства.

В процессе перехода от (6) к (3) и им аналогичных сужений в более общем случае произвольных обратных задач, первоначально присущие им свойства неединственности теряются. Задача «беднеет», ее особые свойства, присущие ей эффекты размываются, становятся не заметными, но их влияние даже в упрощенной форме проявляется, становясь менее очевидным скрытым, слабоуправляемым. Проявление эффектов эквивалентности, присущих общей задаче в задачах искусственно суженых до имеющих единственное решение называется скрытой эквивалентностью.Это специфический для геофизики эффект проявляющийся в геологической содержательности получаемых решений, соответствии тем ожиданиям, «под которые» используемый аппроксимационный модельный класс строился. Эквивалентность, присущая исходной задаче с неединственным решением при сужении задачи, приобретает новые формы. Они проявляются в виде скрытых, не поддающихся контролю эффектов, влияние которых может существенно нарушить содержательность получаемых результатов, о которых речь шла в 1.4. Эта тема ключевая для геофизики, отличающая ее от других задач будет продолжена. Анализ подобного рода эффектов и форм их проявления в сужениях задач совершенно необходим. С этой целью необходимо максимально полно изучить расширенную задачу, где за счет использования аппарата анализа в функциональных пространствах эти эффекты можно более полно изучить. Лишь после этого следует переходить к сужению задачи, рассмотрению ее конечномерных аналогов и изучению свойств этой – упрощенной задачи. Здесь ситуация напоминает ту, которая возникает при рассмотрении сингулярных интегральных уравнений например преобразования Гильберта или Радона. Если их сразу перевести в конечномерную форму – преобразовать к виду системы линейных уравнений, то весьма затруднительно получить формулы обращения. Наоборот, ситуация проясняется при рассмотрении бесконечного случая. Именно в этой связи совершенно необходимо рассмотрению окончательной конечномерной, малоразмерной задачи предварять максимально полный анализа на корректность расширенной, бесконечномерной задачи.

Вернемся к символической записи обратной задачи (1), и определим основные понятия корректности.

Задача:

(3.7)

называется корректной, если:

1. .	(существование);
2. Если из следует .	(единственность);
3. .	(устойчивость).

Условие 1 читается следующим образом: для любого найдется 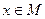,такие, что .

Величина называется модулем непрерывностиобратного оператора к A в норме пространств X, Y на множестве M. Модулем непрерывност (исходного) оператора , действующего из в Y называется:

.

Приведенные условия, называются условиями корректности по Адамару. Их нельзя рассматривать совершенно изолированно. Характеризуя различные аспекты одной и той же задачи, они тесно связаны между с особой.

Существование. С физической точки зрения ясно, что если реально измерено физическое поле, то существуют и источники, его породившие. Однако такое упрощенное решение вопроса о существовании источников поля вовсе не решает вопроса о существовании решения уравнения (7) не только при произвольном , но и при конкретно заданном. Дело в том, что:

1. реально существующее распределение изучаемого параметра может оказаться более сложным и многокомпонентным, чем это «предусмотрено» при формировании аппроксимационной модели M. На M просто нет соответствующего элемента.

2. конкретно заданное поле у неизбежно осложнено ошибками. Сюда относятся собственно ошибки измерений и обработки поля, а также ошибки квантования, возникающие при подготовке наблюдаемой для ввода в ЭВМ. Подобрать модель из M, которая включала бы в себя строго все компоненты, включая и эффекты от ошибок, чаще всего, невозможно, да и неразумно. Но в условиях, когда заведомо неизвестно что связано с ошибкой, а что с полезной компонентой, да и что такое полезная компонента вообще бессмысленно требовать строгой, точной разрешимости уравнения (7);

3. оператор А неизбежно осложнен ошибками. Сюда относится возможная замена сложного закона более простым, но приближенным (например, замена детерминированного закона его статистическим приближением), ошибки приближенного расчета прямого эффекта.

Таким образом, если , то указанные факторы могут привести к тому, что реально заданная наблюдаемая у не принадлежит ImA, и в этом случае уравнение (7) в строгом смысле решения не имеет. Но если либо , то уравнение (7) разрешимо точно либо с любой наперед заданной точностью.

Единственность решенияобратных геофизических задач наиболее, если так можно выразиться, тонкое их свойство. Большинство обратных геофизических задач при своей достаточно общей постановке если и имеют решение, то оно не единственно. Их единственность достигается искусственным сужением задачи на выбранный, чаще всего аппроксимационный модельный класс . Его выбор определяется геофизиком. При этом имеются две противоположные тенденции. С одной стороны, множество желательно сделать как можно шире для того, чтобы повысить его аппроксимационные возможности (см. 1. 3) на более широком множестве элементов. Это делает его более универсальным и пригодным в «непредсказуемых» ситуациях, позволяет лучше аппроксимировать некоторым его (искомым) элементом реальное распределение физического параметра. С другой стороны, возможность расширения задачи ограничена тем, что при достижении определенного уровня этого расширения может случиться, что решение на уже не единственно. Но прежде чем это произойдет, резко возрастает неустойчивость определения параметров того либо иного элемента из . Расширение множества приводит к увеличению числа параметров, посредством которых описывается тот либо иной элемент из . Очевидно следующее утверждение:

Пусть . Тогда: из единственности решения уравнения (7) на следует единственность его решения на и .

Таким образом, при выборе аппроксимационного модельного класса и числа характеризирующих его параметров необходимо держатся некоторого, не всегда ясного оптимума. Различие же геологических ситуаций вынуждает рассматривать множество аппроксимационных классов моделей, для каждого из которых следует доказать свое теорему единственности. Содержание последней состоит в том, что в ней формируется условия и ограничения на множество М, при которых обратная задача на этом множестве, если имеет решение, то оно единственно. На самом деле доказательством теоремы единственности проблема единственности не решается. Она лишь переходит в иную плоскость. Из проблемы существования многих решений трансформируется в проблему адекватности получаемого единственного решения реальности.

Доказательство теорем единственности для тех либо иных модельных классов является, как правило, сложной задачей, выполнимой лишь при некоторых упрощающих дело предположениях. Для примера см. теорему 7 настоящего раздела. Прежде всего, это относится к предположением о способе задания наблюдаемых. Так, в задачах гравиметрии и магнитометрии к таким предположениям относится то, что поле заданно всюду на некоторой плоскости, или даже заданно нормальная производная потенциала на границе регулярной области, охватывающей возмущающие массы. Практически отсутствуют теоремы, учитывающие дискретность задания поля, а так же наличие погрешностей в его задании. Таким образом, в вопросе о единственности решения обратной задачи есть три аспекта. Первый- это формально математическая единственность – однозначная разрешимость уравнения (7) на множестве . Второй – единственность реально решаемой задачи, учитывающая приближенность задания наблюдаемой, оператора. Третий – проблема адекватности получаемого единственного решения реальности или тому, «в надежде на поучение которого» модельный класс конструировался. Этот третий аспект является основным для интерпретационного процесса.

Устойчивостьхарактеризует степень изменения решения при изменении входных данных. Она характеризуется модулем непрерывности обратного к оператора: . Эта величина ассоциируется с нормой обратного к оператора действующего из X в Y, суженного на множество . Чем меньше эта величина, тем более устойчиво по отношению к изменению исходных данных – физических полей. Если наличие небольших погрешностей в правой части уравнения приводит к коренной перестройке решения, то такое решение вряд ли представляет существенный интерес, хотя и может оказаться полезным для оценки некоторых интегральных характеристик решения.

Устойчивость, непрерывность того либо иного оператора существенно зависит от вводимой топологии. Так, например, при решении многих обратных задач необходимо дифференцировать наблюдаемую. Такая процедура возникает при интерпретации данных сейсморазведки, когда необходимо вычислить градиенты годографа, связанные со скоростью (кажущейся) распространения сейсмических волн. Такая же ситуация возникает и при трансформации гравитационных и магнитных полей (расчет высших производных потенциала). Дифференцирование непрерывно из С¹ в С либо L₂, но не является таковым из L₂ в С. Однако и в этом вопросе следует различать две стороны – формально математическую и содержательную. Если модуль непрерывности обратного оператора равен некоторому большому, но к конечному числу (например, 100, 1000), то с формально математической точки зрения задача устойчива. Но с содержательной точки зрения в этом случае влияние погрешностей в наблюдаемой на результат решения будет столь велико, что решение может оказаться непригодным для геологических выводов и в вычислительном отношении должно рассматриваться как неустойчивое. Другой предельный случай – когда это число очень мало (например, 0,01, 0,001). В этом случае не только помеха, но и полезная компонента уже будут мало сказываться на решении. Ясно, что и такое решение может оказаться непригодным для целей интерпретации. Для характеристики задачи в целом используется обусловленность задачи: .

Следует признать, что с позиций приведенного определения корректности, обратные задачи геофизики по большей части некорректны во всех смыслах. В них не выполнено первое условие корректности, и в строгом смысле решение не существует. В них не выполнено второе условие и решение, даже если оно существует неединственно. Наконец обратные задачи геофизики по большей части неустойчивы.

Наиболее развитыми являются теория и методы решения линейных некорректных задач, в которых не выполнено третье условие – они неустойчивы. Для такого класса задач введен даже специальный термин - условно корректные или корректные по Тихонову задачи. Центральным вопросом при их рассмотрении является свойство устойчивости или, что почти то же самое, непрерывности, ограниченности обратного оператора на тех либо иных сужениях исходной задачи. В этой связи в теории условно корректных задач усиленно используются математические результаты, касающиеся свойств непрерывности преобразований – теорема о гомеоморфизме и близкие результаты. Основная идея решения неустойчивых задач состоит в том, чтобы заменить исходную задачу с неограниченным обратным оператором на другую – приближенную, но с ограниченным. Собственно вся теория регуляризации, направленная на решение неустойчивых задач как раз и состоит в изучении свойств непрерывности малых вариаций к исходной задаче. При этом требуется еще, чтобы эти малые вариации не уводили результат слишком далеко от некоторого предполагаемого истинного решения, существование которого при некоторых точных данных – физических полях предполагается[4].

Условия существования решений (разрешимости уравнения) и их устойчивости связаны между собой. Условие разрешимости для любого означает, что множество значений оператора совпадает со всем Банаховым пространством 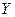. Но для линейных ограниченных операторов, действующих в паре пространств X,Y (A: X→Y), из последнего условия следует ограниченность обратного к оператора, т.е. устойчивость обратной задачи. Точнее, справедлив такой результат.

Теорема 1.Пусть А – линейный ограниченный взаимно-однозначный оператор из X в Y, где X, Y- банаховы пространства. Для того чтобы , необходимо и достаточно: .

Приведенный результат есть очевидное следствие теоремы 2 из. Пр 2..4. Действительно, ограниченное преобразование есть одновременно и замкнутое. Банахово пространство есть множество второй категории в себе, и все условия указанной теоремы выполнены.

Следующая модификация того же результата может оказаться более полезной.

Следствие. Еcли А – замкнутый взаимно-однозначный оператор из X в Y, и ImA содержит внутреннюю точку, то и . Этот результат становится очевидным, если заметить, что множество, имеющее внутреннюю точку, есть множество второй категории (прил.2). Необходимо обратить внимание на то, что хотя в формулировке теоремы 1 и следствия из нее присутствовало требование единственности решения обратной задачи – эти условия на самом деле изначально, в полной формулировке независимы. Смешение эффектов неединственности и неустойчивости и возникновение ситуации, при которой неустойчивость становиться практическим проявлением неединственности при вычислениях происходит большей частью от неверного сужения задачи. Чтобы показать это, проведем следующие рассмотрения.

Для линейного ограниченного оператора определим фактор пространствопространства по ядру оператора . Оно состоит из классов (смежности),содержащих вместе со всяким элементом и все элементы , где . Совокупность элементов, образующих этот класс смежности обозначим . Норму элемента определим равенством: Тогда есть обычное Банахово пространство, и оператор взаимнооднозначен из в 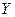. В такой формулировке задача нахождения класса смежности соответствующего заданному полю:

или, что эквивалентно, решение задачи:

попадает под условия теоремы 1. Условие единственности подобным приемом «разведено» с условием устойчивости. Они оказались независимыми, самостоятельными и несводимыми один к одному. К сожалению, однако, этот результат носит более академический, чем конструктивный характер. Из него можно вывести много красивых следствий о свойствах плотности области значений операторов в тех либо иных функциональных пространствах. Эти результаты дают понимание причины многих эффектов, но, чаще всего, не дают конструктивных способов решения некорректных задач.

Наиболее полно теория некорректных задач развита для случаев линейного оператора прямой задачи. В то же время многие задачи, а возможно и их большая часть являются нелинейными. Арсенал средств анализа и решения последних существенно уже. Основным приемом их рассмотрения служит линеаризация. Пример линеаризации исходной нелинейной задачи уже был приведен – это рассмотренные в гл. 2 методы сейсмической томографии. По большей части нелинейными оказываются все задачи с использованием геометрических структурных моделей. Здесь линеаризация необходимый элемент. Сущность приемов линеаризации состоит в том, что рассматриваются в качестве искомых физических параметров их приращения относительно некоторого известного уровня (переменного). Например, рассматриваются приращения горизонтов относительно заданного уровня – нулевого приближение. Тогда уравнения относительно этих приращений оказываются, с точностью до членов меньшего порядка малости, чем эти приращения, линейными – это уравнения дифференциалов. Вот эти линеаризованные уравнения и рассматриваются. При необходимости процесс линеаризации повторяется в окрестности нового – уточненного распределения параметров, и весь процесс нахождения нового приращения выполняется заново. Конечно, процесс линеаризации вносит свои погрешности, которые в условиях некорректности (неустойчивости) могут играть чрезмерно большую роль. Однако, ничего иного, по всей видимости, делать не остается. Общие рекомендации по процедурам линеаризации, конечно, могут быть даны, однако этому мы предпошлем рассмотрение конкретных задач

Вопросы, связанные с существованием, единственностью, устойчивостью решения обратных задач, являются основой, составляющей предмет теория некорректных задач в геофизике. Они тесно переплетаются с другими, такими как повышение интерпретационных возможностей геофизических методов, оценка точности получаемого решения.

Традиционно в геофизике сложилось мнение, согласно которому задачи, имеющие неединственное решение, если так можно выразиться – “недоработанные” задачи. Иными словами, необходимо сначала надлежащим сужением модельного класса эти задачи свести к задачам с единственным решением, и уж затем решать эту новую полученную задачу. Точно так же принято считать, что обязательно должна быть оценена точность полученного решения. Вплоть до признания бесполезным какого-либо результата, если точность его не оценена. Несомненно, если в задаче выполнимо первое и второе, то это преимущество. Однако следует всегда иметь в виду, что изначальная формулировка обратных задач, их, если так можно сказать, полная формулировка, приводит к задачам, имеющим неединственное и неустойчивое решение. В этом случае может оказаться, что единственность достигается в ущерб геологической содержательности, а точность будет тем выше, чем дальше решение находится от реального объекта, чем “грубее” аппроксимация найденным решением реального объекта.

Представим себе, например, что изучается изолированная гравитационная аномалия и решается для неё обратная задача для точечного источника. Иными словами, ищется полная масса и координаты центра тяжести тела. Точность решения будет весьма высока (за счет того, что модельный класс узок). Но найденный таким образом шар (если плотность известна), как правило, будет весьма далек от реального объекта. Полученная высокая точность решения обратной задачи ничего общего не имеет с точностью по существу, с точностью построения физического объекта. Чтобы повысить последнюю, следует расширить модельный класс, а это автоматически приведет к ухудшению точности решения обратной задачи, поскольку задача приближается к неустойчивой. Дальнейшее повышение соответствия выбранного модельного класса реальной среде последовательно приводит к задачам неустойчивым, в которых вообще нельзя говорить о точности решения, и задачам неединственным (с неединственным решением), в которых такое понятие становится совершенно бессодержательным. Таким образом, можно говорить о точности определения параметров моделей в заданном модельном классе. Это внутренняя точность используемой технологии извлечения информации – некоторая кажущаяся, эффективная точность. Но не в коем случае эту точность нельзя без оговорок переносить на точность по существу – точность реконструкции физической модели и, тем более геологических построений. Точно так же, обеспечив надлежащим сужением модельного класса единственность решения обратной задачи, не следует забывать, что достигаемая в этом случае единственность это всего лишь единственность математической задачи, а не единственность по существу.

3.2. Аппроксимационные модели и принцип квазирешений.

Обратные задачи геофизики, состоящие в реконструкции физической модели среды по физическим полям или наблюдаемым, естественным образом формулируются как задачи, решение которых не единственно. Выбор сужения для обеспечения единственности - это искусственный прием, направленный на получение конструктивных результатов. Сужение задачи, введение узких аппроксимационных модельных классов направлено на обеспечение единственности, но это же неизбежно ведет к ошибкам в аппроксимации, а зачастую и к потере содержательности результата.

Рассмотрим задачу:

(3.8)

где X, Y – банаховы пространства. Считаем, что для нее не выполнено ни одно из условий корректности по Адамару. Следует так переформулировать (8), чтобы решение ее существовало при любой правой части, было единственным и устойчивым к ошибкам как во входных данных (наблюдаемой), так и в операторе А.

Определение 1. классом эквивалентностидля элемента называется множество .

Все множество 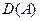разбивается на непересекающиеся классы эквивалентности (ср. с построением фактор-пространства выше и в приложении прил. 2.4). Если А - линейный ограниченный оператор, то - замкнутое линейное подпространство в X, и построенные классы эквивалентности есть ни что иное, как классы смежности фактор-пространства .

Определение 2. Классом единственностидля оператора А называется такое подмножество М в , что из условий и следует .

Следующее свойство класса единственности непосредственно следует из определения.

Каждое из перечислений класса единственности с каждым из классов эквивалентности для всех содержит не более одного элемента.

Теорема 2. Пусть – компакт, являющийся классом единственности. Тогда из условий и следует: .

Доказательство. В соответствии с теоремой о гомеоморфизме (пр.2.3), взаимно-однозначный и непрерывный оператор, определенный на компакте, имеет ограниченный обратный. Это означает, что обратный к оператору , суженному на (оператор ), переводит каждое ограниченное множество в снова ограниченное, и из конечности следует конечность для любых . Но это эквивалентно тому, что:

_.

Отсюда и следует требуемое утверждение.

По сути, конструктивная часть утверждения состоит в том, что обратная задача, соответствующая сужению ограниченного оператора (вполне достаточно только замкнутого) на класс единственности, являющийся компактом (например, любое ограниченное замкнутое подмножество конечномерного пространства) имеет устойчивое решение. Однако эта устойчивость, как это уже подчеркивалось выше, может носить формальный характер.

Определение 3. Квазирешением уравнения 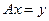на множестве называется элемент , минимизирующий на М невязку[5]:

. (3.9)

Приведенное определение дает одновременно и конструктивный способ построения квазирешения, состоящий в минимизации невязки. Для этого могут быть использованы как прямые, численные методы минимизации, так и аналитические приемы (см. приложение).

Пусть образ множества при отображении А есть , и пусть N – сильно выпуклое, замкнутое в Y множество. Тогда для элемента y, вообще говоря, не принадлежащего N, существует его проекция на N:

.

Квазирешение на элементе (заданном физическом поле y) можно представить себе не как прообраз y, который (прообраз, если он существует) не принадлежит, вообще говоря, М, а как прообраз проекции элемента y на N, который уже не только существует (поскольку по определению), но и принадлежит М. Таким образом, условия на множество М и оператор А, обеспечивающие:

а)взаимно – однозначность и взаимно – непрерывность оператора А, суженного на М;

б)существование и единственность проекции произвольного элемента на ,

являются достаточными для того, чтобы задача поиска квазирешения была корректной по Адамару.

Непрерывность оператора проектирования обеспечивает следующая

Теорема 3[6]. Оператор проектированияв нормированном пространстве (на самом деле достаточно, чтобы пространство было только метрическим) на произвольное множество N является равномерно непрерывным по переменной y.

Приведенный результат означает следующее: ,