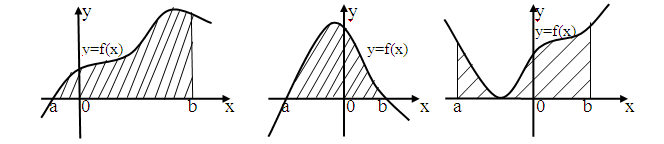Ход практического занятия.
1.Формулирование темы занятия, пояснение связи темы с другими темами учебной дисциплины;
2.Проверка готовности студентов к занятию;
3.Проведение непосредственно занятия согласно тематике и в соответствии с рабочей программой дисциплины:
›Изучить теоретический материал по теме «метод интегрирования по частям»
›Рассмотреть примеры решения типовых заданий.
›Выполнить самостоятельную работу .
›Ответить на контрольные вопросы.
Краткий теоретический материал


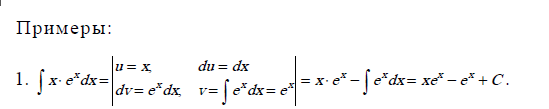
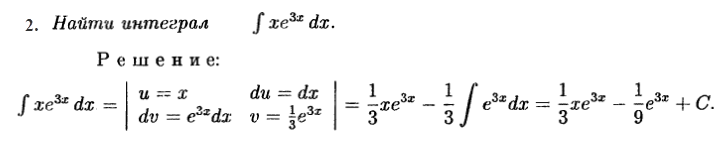


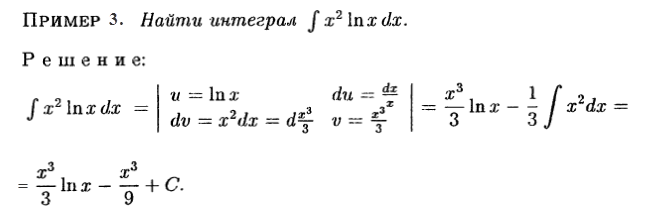

Задание выполняемые студентами на доске
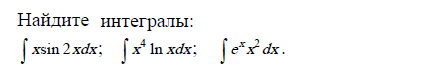
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Найдите интегралы методом интегрирования по частям:
Вариант 1.
1. 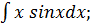 2.
2. 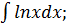 3.
3. 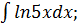 4.
4. 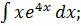 5.
5. 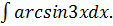
Вариант 2.
1. 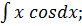 2.
2. 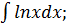 3.
3. 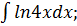 4.
4. 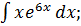 5.
5. 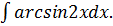
Вопросы.
1. Запишите формулу интегрирования по частям.
2. Запишите пять любых интегралов в общем виде, для которых применяется формула интегрирования по частям.
3. Выберите из них любые две, и запишите, что обозначается в них через u, а что через dv.
Практическое занятие №8
Тема:Вычисление площадей фигур с помощью определенных интегралов.
Цель: Проверить на практике понятие определённого интеграла, умение вычислять определённый интеграл по формуле Ньютона-Лейбница. Умение вычислять площадь фигур с помощью определенных интегралов. Закрепление умений и навыков решения прикладных задач с помощью определённого интеграла.
Задачи:
• развитие творческого профессионального мышления;
• познавательная мотивация;
• овладение языком науки, навыки оперирования понятиями;
• овладение умениями и навыками постановки и решения задач;
• углубление теоретической и практической подготовки;
• развитие инициативы и самостоятельности студентов.
Обеспечение практического занятия:
Теоретический материал методической рекомендации к практической работе.
Учебник. Богомолов Н.В. «Математика». – М.: Дрофа, 2009.
Индивидуальные карточки с вариантом практической работы.
Ход практического занятия.
1.Формулирование темы занятия, пояснение связи темы с другими темами учебной дисциплины;
2.Проверка готовности студентов к занятию;
3.Проведение непосредственно занятия согласно тематике и в соответствии с рабочей программой дисциплины:
›Повторить теоретический материал по теме «Вычисление площадей фигур с помощью определенных интегралов»
›Рассмотреть примеры решения типовых заданий.
›Выполнить самостоятельную работу.
›Ответить на контрольные вопросы.
Теоретический материал
 Примеры криволинейных трапеций приведены на рисунках.
Примеры криволинейных трапеций приведены на рисунках.