РОЗВ’ЯЗАННЯ СЛАР ТА ОЦІНКА ТОЧНОСТІ ОТРИМАНОГО НАБЛИЖЕНОГО РОЗВ’ЯЗКУ

Після врахування граничних умов результуюча СЛАР буде пов­ністю сформована і залишається знайти її розв’язок, наприклад викорис­то­вуючи вбудовану функцію MATHCAD lsolve. Якщо були задані го­ловні граничні умови, то, в силу вище описаного алгоритму їх вра­ху­ван­ня, потрібно ще також відповідним чином модифікувати вектор вузло­вих значень (див. функцію AddNodalValueOnLeftSide(a,g,U,N) на рис. 6.).

Оскільки для крайової задачі (20)-(21) при 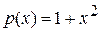, , 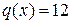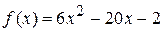можна отримати точний розв’язок ( 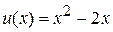), то тут же наведено його порівння з апроксимацією за МСЕ на сітці з чотирьох скінченних елементів.

КОНТРОЛЬНІ ЗАПИТАННЯ

1. Що таке нев’язка? У чому полягає основна ідея методу зважених нев’язок? Запишіть систему рівнянь методу зважених нев’язок.

2. У чому суть методу Гальоркіна як варіанта методу зважених нев’язок? Якими перевагами володіє метод Гальоркіна?

3. Здійсніть слабке формулювання методу Гальоркіна. Які переваги воно дає?

4. У чому полягають основні ідеї методу скінченних елементів?

5. Що таке умови гладкості на базисні функцій МСЕ? Чому базисні функції повинні задовільняти ці умови?

6. З яких етапів складається загальна схема розв’язування крайових задач методом скінченних елементів?

7. Які граничні умови називаються природними? Як вони вико­ну­ються в МСЕ?

8. Що таке головні граничні умови? Яким чином вони задовіль­ня­ють­ся в МСЕ?

ЛАБОРАТОРНЕ ЗАВДАННЯ

1. Ознайомитися з основними поняттями та етапами розв’язання крайових задач методом скінченних елементів.

2. Знайти розв’язок крайової задачі

,

, .

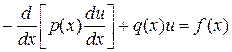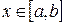
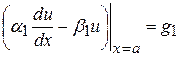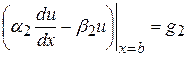Індивідуальні завдання наведені в Додатку. Дослідити збіжність числового розв’язку при згу­щенні сітки.

3. Побудувати графіки функцій отри­маного наближеного розв’язку та за­да­ного точного розв’язку крайової задачі.

4. Оформити і здати звіт про виконання лабораторної роботи.

ЗМІСТ ЗВІТУ

1. Мета роботи.

2. Короткі теоретичні відомості.

3. Постановка задачі індивідуального завдання.

4. Оформлений належним чином (з коментарями, поясненнями та результатами) документ MATHCAD з програмою розв’язання завдання.

5. Аналіз результатів та висновки.

СПИСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ

1. Зенкевич О., Морган К. Конечные элементы и аппрок­си­ма­ция. - М.: Мир, 1986. - 318 с.

2. Стренг Г., Фикс Дж. Теория метода конечных элементов. –М.: Мир, 1977. – 349 с.

3. Молчанов И.Н., Николенко Л.Д. Основы метода конечных элементов. -К.: Наук.думка, 1989. - 272 с.

4. Савула Я.Г. Числовий аналіз задач математичної фізики ва­ріа­цій­ними методами. –Львів: видавничий центр ЛНУ ім.Івана Франка, 2004. – 221 с.

5. В.Дьяконов. MATHCAD 8/2000: специальный справочник. – СПб: Питер,2001. -592 с.

ДОДАТОК