Алгоритм метода потенциалов

Числа u_i (i=1, 2, …, m) и v_j (j=1, 2, …, n) из Теоремы 8.2.5 называются потенциалами задачи. Метод потенциалов основан на использовании этих чисел.

8.3.1. Основные пункты алгоритма:

1) Построить первоначальный опорный план.

2) Проверить план на оптимальность. Если критерий оптимальности не выполнен, то перейти к пункту 3). В противном случае задача решена. Перейти к пункту 5).

3) Перейти к очередному опорному плану.

4) Перейти к пункту 2).

5) Вычислить стоимость перевозок.

Распишем подробно основные пункты алгоритма.

8.3.2. Построение первоначального опорного плана.

Мы познакомимся с двумя методами построения первоначального опорного плана.Мы здесь рассмотрим метод северо-западного угла (ниже, в пункте 8.3.5 познакомимся с так называемым методом наименьшей стоимости). Суть метода (северо-западного угла) поясним на задаче с Таблицей 8.1. Начинаем заполнять таблицу планом с «северо-западного угла».

Пример 4. У первого поставщика имеется 90 единиц груза, а первому потребителю нужно 70 единиц. Поэтому можем спланировать перевозку 70 единиц груза от первого поставщика к первому потребителю: вписываем в клетку (1, 1) 70 и как бы вычёркиваем первого потребителя - он «получил своё» и в дальнейшем распределении груза не участвует: ставим знак «-» над первым столбцом:

bj ai	-

У первого поставщика осталось 20 единиц груза, а второму потребителю всего нужно 30. Поэтому вписываем эти 20 единиц в клетку (1, 2), вычеркнув первую строку (у первого поставщика все 90 единиц груза использованы, и он выбывает из дальнейшего распределения поставок):

bj ai	-
-

Второму потребителю требуется ещё 10 единиц, которые мы «заберём» у второго поставщика (у него их имеется 30 единиц): вписываем 10 в клетку (2, 2) и вычеркнем второй столбец:

bj ai	-	-
-

У второго поставщика осталось ещё 20 единиц груза, и третьему потребителю требуется как раз 20 единиц. Вписав эти 20 единиц в клетку (2, 3) вычёркиваем только одного участника, скажем, второго поставщика, хотя фактически из распределения груза выбывают одновременно второй поставщик и третий потребитель. Вычёркивание на одном шаге только одного участника обеспечивает участие второго в следующем шаге заполнения таблицы, и в результате будет заполнено в точности m+n-1 клеток:

bj ai	-	-
-
-

Так как третий потребитель ещё не вычеркнут, то вписываем 0 в клетку (3, 3) и вычёркиваем третьего потребителя:

bj ai	-	-	-
-
-

Наконец, на последнем, 3+4-1=6-м шаге, вписываем 40 в клетку (3, 4) и вычёркиваем обоих участников - третьего поставщика и четвёртого потребителя:

bj ai	-	-	-	-
-
-
-

Получили первоначальный опорный план (Таблица 8.2).

8.3.3. Проверка плана на оптимальность производится по следующей схеме:

1) Вычислить потенциалы u_i (i=1, 2, …, m) и v_j (j=1, 2, …, n).

2) Проверить условие оптимальности (8.3).

Более подробно:

1) Потенциалы вычисляются решением системы (8.2), где c_ij - стоимости перевозок для заполненных клеток. Эта система состоит из m+n уравнений с m+n неизвестными. Ранг системы равен m+n-1, так как матрица этой системы транспонирована по отношению к матрице ограничений транспортной задачи (8.1), ранг которой равен m+n-1 (Теорема 8.2.2). Поэтому эта система имеет одну свободную неизвестную, и, вообще говоря, имеет бесконечное множество решений. Присвоив какой-то неизвестной, скажем, неизвестной u₁, какое-то значение, например, 0 (u₁=0), мы найдём однозначно определённые значения остальных u_i и v_j. При этом удобно решать систему не традиционным способом (например, методом исключения Гаусса), а, так сказать, «не отходя от таблицы»: справа от таблицы на уровне соответствующей строки последовательно выписываем очередное найденное значение u_i, а под соответствующим столбцом - очередное найденное значение v_j. Продемонстрируем это на нашем примере (Таблица 8.1). А именно,

Пример 5. Найдём потенциалы u_i и v_j для первоначального опорного плана (Таблица 8.2).

Справа от таблицы на уровне первой строки записываем 0:

bj ai

В первой строке заполнены клетки (1, 1) и (1, 2). Стоимости в этих клетках равны соответственно c₁₁=1 и c₁₂=3. Поэтому v₁=c₁₁-u₁=1-0=1 и v₂=c₁₂-u₁=3-0=3. Значения v₁=1 и v₂=3 записываем под первым и вторым столбцами соответственно:

bj ai

Во втором столбце кроме клетки (1, 2) заполнена клетка (2, 2). По ней определяем u₂=c₂₂-v₂=3-3=0. Записываем u₂=0 справа от таблицы на уровне второй строки:

bj ai

Во второй строке кроме клетки (2, 2) заполнена клетка (2, 3). По ней определяем v₃=c₂₃-u₂=1-0=1. Записываем значение v₃=1 под третьим столбцом:

bj ai

В третьем столбце кроме клетки (2, 3) заполнена клетка (3, 3). По ней определяем u₃=c₃₃-v₃=4-1=3, и записываем u₃=3 справа от таблицы на уровне третьей строки:

bj ai

Наконец, по клетке (3, 4) определяем v₄=c₃₄-u₃=2-3=-1, и записываем его под четвёртым столбцом:

bj ai
				-1

Таким образом, u₁=0, u₂=0, u₃=3, v₁=1, v₂=3, v₃=1, v₄=-1.

2) После нахождения потенциалов u_i (i=1, 2, …, m) и v_j (j=1, 2, …, n) необходимо проверить выполнение условия (8.3) для всех пустых клеток (для заполненных клеток потенциалы найдены из условия u_i+v_j=c_ij; поэтому для заполненных клеток проверка условия (8.3) нужна разве что только для проверки правильности найденных потенциалов. Имеем

u₁+v₃=0+1=1<4=c₁₃, u₁+v₄=0-1=-1<5=c₁₄, u₂+v₁=0+1=1<5=c₂₁,

u₂+v₄=0-1=-1<2=c₂₄, u₃+v₁=3+1=4>2=c₃₁, u₃+v₂=3+3=6>1=c₃₂,

Таким образом, u₁+v₃<c₁₃, u₁+v₄<c₁₄, u₂+v₁<c₂₁, u₂+v₄<c₂₄, но u₃+v₁>c₃₁ и u₃+v₂>c₃₂, то есть условие (8.3) выполнено не для всех клеток, и нельзя утверждать, что данный опорный план оптимален.

8.3.4. Переход к новому опорному плану (построение очередного опорного плана).

Для перехода к другому опорному плану (построения очередного опорного плана) поступают следующим образом:

1) Находят оценки D_ij=u_i+v_j-c_ij для клеток (i, j), в которых условие (8.3) нарушается.

2) Выбирают клетку с максимальным из них (по Теореме 8.2.6 это обеспечивает максимальное уменьшение значения целевой функции).

3) Строят помеченный цикл из выбранной (пустой) клетки. Если клеток с максимальным D_ij>0 несколько, то выбирают ту, в которой стоимость перевозок наименьшая. Если и таких клеток несколько, то выбирают любую.

4) Из выбранной клетки осуществляют сдвиг по циклу.

Пример 6. В нашем примере:

1) Найдём оценки для клеток для клеток (i, j), в которых условие (8.3) нарушается (напоминаем, что u₃+v₁>c₃₁ и u₃+v₂>c₃₂, и условие (8.3) нарушается в клетках (3, 1) и (3, 2)): D₃₁=u₃+v₁-c₃₁=3+1-2=2, D₃₂=u₃+v₂-c₃₂=3+3-1=5.

2) Выбираем клетку с максимальным из D_ij>0: Это - (3, 2): D₃₂>D₃₁.

3) Из клетки (3, 2) строим помеченный цикл:

bj ai
		-	+
		+	-
				-1

4) Осуществляем сдвиг по циклу: минимальное содержимое клеток со знаком «-» оказалось равном 0, то есть этот 0 мы будем вычитать из клеток со знаком «-» и прибавлять в клетки со знаком «+». Фактически опорный план не изменится, но изменится система заполненных клеток (что тоже влияет на ход решения задачи!):

bj ai

Далее мы доведём решение задачи до конца:

2.1) Найдём потенциалы. Сначала присваиваем u₁=0 и по заполненным клеткам первой строки определяем v₁=c₁₁-u₁=1-0=1 и v₂=c₁₂-u₁=3-0=3. Теперь по заполненным клеткам второго столбца (а они оказались заполненными все) определяем u₂=c₂₂-v₂=3-3=0 и u₃=c₃₂-v₂=1-3=-2. Далее, по заполненной клетке второй строки определяем v₃=c₂₃-u₂=1-0=1. Наконец, по заполненной клетке третьей строки определяем v₄=c₃₄-u₃=2-(-2)=4. Найденные потенциалы записываем в клетках справа и снизу таблицы:

bj ai
					-2

2.2) Проверяем условие оптимальности для пустых клеток:

u₁+v₃=0+1<4=c₁₃, u₁+v₄=0+4<5=c₁₄, u₂+v₁=0+1<5=c₂₁,

u₂+v₄=0+4>2=c₂₄, u₃+v₁=-2+1<2=c₃₁, u₃+v₃=-2+1<4=c₃₃,

и условие оптимальности нарушается в единственной клетке (2.4).

2.3) Строим помеченный цикл из клетки (2, 4):

bj ai
		10 -		+
		+		-	-2

2.4) Имеем m= 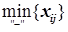= =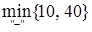10. Эти 10 единиц вычитаем из клеток со знаком «-» и прибавляем в клетки со знаком «+». Получаем очередной опорный план:

bj ai

3.1) Ищем потенциалы: u₁=0, v₁=c₁₁-u₁=1-0=1 и v₂=c₁₂-u₁=3-0=3, u₃=c₃₂-v₂=1-3=-2, v₄=c₃₄-u₃=2-(-2)=4, u₂=c₂₄-v₄=2-4=-2, v₃=c₂₃-u₂=1-(-2)=3:

bj ai
					-2
					-2

3.2) Проверяем условие оптимальности для пустых клеток:

u₁+v₃=0+1<4=c₁₃, u₁+v₄=0+4<5=c₁₄, u₂+v₁=-2+1<5=c₂₁,

u₂+v₂=-2+3<3=c₂₄, u₃+v₁=-2+1<2=c₃₁, u₃+v₃=-2+3<4=c₃₃.

Таким образом, условие оптимальности u_i+v_j£c_ij выполнено, то есть данный план оптимален. Вычислим, во сколько обойдутся перевозки при данном плане: 70×1+20×3+20×2+10×2+10×1+50×2=320.

Ответ: Матрица перевозок: 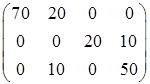. Стоимость перевозок F_min=320 у.е.

8.3.5. Метод наименьших затрат построения первоначального опорного плана.

Так же, как и с методом северо-западного угла, с методом наименьших затрат построения первоначального опорного плана познакомимся на конкретном примере задачи Таблицы 8.1. В отличие от метода северо-западного угла, в этом методе на очередном шаге из оставшихся клеток заполняется клетка с самыми дешёвыми перевозками. Но, как и в методе северо-западного угла, на каждом шаге, за исключением последнего, вычёркивается только один участник.

Наименьшая стоимость перевозок - в клетках (1, 1), (2, 3) и (3, 2). Заполняем, по возможности, эти клетки, вписывая соответственно 70, 20 и 30, и вычёркивая соответственно первый, третий и второй столбцы:

bj ai	-	-	-

Из оставшихся клеток наиболее дешёвыми являются клетки (2, 4), (3, 1) и (3, 4) со стоимостями c₂₄=c₃₁=c₃₄=2. Клетка (3, 1) не может участвовать при заполнении плана, так как первый столбец вычеркнут. В клетку (2, 4) вписываем 10 (так как у второго поставщика осталось только 10 единиц груза), вычеркнув второго поставщика, и клетку (3, 4) вписываем 10 (так как у третьего поставщика также осталось 10 единиц груза, а четвёртому потребителю требуется ещё 30 единиц груза), вычеркнув третьего поставщика:

bj ai	-	-	-
-
-

Невычеркнутыми, остались первая строка и последний столбец, что означает, что осталось заполнить только одну клетку (1, 4). Вписываем в неё 20:

bj ai	-	-	-	-
-
-
-

8.3.6. В заключение пункта 8.3 резюмируем алгоритм метода потенциалов:

1) Построить первоначальный опорный план.

2) Проверить план на оптимальность. Для этого:

2.1) Вычислить потенциалы u_i (i=1, 2, …, m) и v_j (j=1, 2, …, n).

2.2) Проверить условие оптимальности u_i+v_j=c_ij (i=1, 2, …, m, j=1, 2, …, n). Если критерий оптимальности не выполнен, то перейти к пункту 3). В противном случае задача решена. Перейти к пункту 5).

3) Перейти к очередному опорному плану. Для этого:

3.1) Найти оценки D_ij=u_i+v_j-c_ij для клеток (i, j) u_i+v_j>c_ij.

3.2) Выбрать клетку с максимальным D_ij>0.

3.3) Из выбранной клетки построить помеченный цикл.

3.4) Осуществить сдвиг по циклу.

4) Перейти к пункту 2).

5) Вычислить стоимость перевозок.

Пример 6. Решить транспортную задачу. Первоначальный опорный план построить методом наименьших затрат.

bj ai

Решение. 1) Построим первоначальный опорный план (методом наименьших затрат). Самые дешёвые перевозки - в клетках (1, 2), (2, 1) и (2, 4). Из них по полной «загрузим» первые две, после чего оставшиеся 20 единиц груза второго поставщика впишем в клетку (2, 4):

bj ai	-
-
-

Из оставшихся клеток самыми дешёвыми являются перевозки со стоимостью 4. Из всех клеток с этой стоимостью не вычеркнутой является клетка (3, 2), куда вписываем 10 (второму ещё потребителю требуется 10 единиц груза):

bj ai	-	-
-
-

Из оставшихся двух невычеркнутых клеток (3, 3) и (3, 4) сначала вписываем в клетку (3, 4) 20 (так как она дешевле клетки (3, 3), и четвёртому ещё требуется 30 единиц груза, а у третьего поставщика их 80 единиц), а затем остальные 50 вписываем в клетку (3, 3):

bj ai	-	-		-
-
-

2¹) Проверим план на оптимальность. Для этого

2.1¹) Найдём потенциалы:

bj ai

Присваиваем u₁=0 и по заполненной клетке (1, 2) первой строки определяем v₂=c₁₂-u₁=3-0=3. По заполненной клетке (3, 2) второго столбца определяем u₃=c₃₂-v₂=4-3=1. Далее, по заполненным клеткам (3, 3) и (3, 4) третьей строки определяем v₃=c₃₃-u₃=6-1=5 и v₄=c₃₄-u₃=5-1=5. Теперь по заполненной клетке (2, 4) второй строки определяем u₂=c₂₄-v₄=4-3=1. Наконец, по заполненной клетке (2, 1) второй строки определяем v₁=c₂₁-u₂=3-1=2.

2.2¹) Проверяем условие оптимальности для пустых клеток:

u₁+v₁=0+2<6=c₁₁, u₁+v₃=0+5>4=c₁₃, u₁+v₄=0+4=4=c₁₄,

u₂+v₂=1+3=4=c₂₂, u₂+v₃=1+5>5=c₂₃, u₃+v₁=1+2<4=c₃₃,

и условие оптимальности нарушается в клетках (1, 3) и (2, 3): u₁+v₃>c₁₃, u₂+v₃>c₂₃.

3.1¹) Вычисляем оценки клеток, в которых нарушается условие оптимальности (D₁₃=u₁+v₃-c₁₃=0+5-4=1, D₂₃=u₂+v₃-c₂₃=1+5-5=1).

3.2¹) Оценки оказались одинаковыми: выбираем клетку с наименее дешёвыми перевозками.

3.3¹) Строим помеченный цикл из выбранной клетки (1, 3):

bj ai
		50 -	+
		+	-

3.4¹) Перемещаем по циклу 50 единиц груза. Получили очередной опорный план:

bj ai

2²) Проверим план на оптимальность. Для этого

2.1²) Найдём потенциалы. Присваиваем u₁=0 и по заполненной клетке (1, 3) первой строки определяем v₃=c₁₃-u₁=4-0=3. По заполненной клетке (3, 3) третьего столбца определяем u₃=c₃₃-v₃=6-4=2. Далее, по заполненным клеткам (3, 2) и (3, 4) третьей строки определяем v₂=c₃₂-u₃=4-2=2 и v₄=c₃₄-u₃=5-2=3. Теперь по заполненной клетке (2, 4) второй строки определяем u₂=c₂₄-v₄=3-3=0. Наконец, по заполненной клетке (2, 1) второй строки определяем v₁=c₂₁-u₂=3-0=3:

bj ai

2.2² - 3.3²) Проверяем условие оптимальности для пустых клеток:

u₁+v₁=0+3<6=c₁₁, u₁+v₂=0+2<3=c₁₃, u₁+v₄=0+3<4=c₁₄,

u₂+v₂=0+2<4=c₂₂, u₂+v₃=0+4<5=c₂₃, u₃+v₁=2+3>4=c₃₃,

и условие оптимальности нарушается в единственно клетке (3, 1), из которой строим помеченный цикл.

bj ai
	40 -			+
	+			-

3.4²) Осуществляем сдвиг по циклу:

bj ai
				+

2³) Проверим план на оптимальность.

2.1³) Найдём потенциалы:

bj ai

2.2³) Проверив условие оптимальности, убеждаемся, это условие выполнено, и задача решена.

5) Вычисляем стоимость перевозок:

50×4+10×3+50×3+30×4+60×4=740.

Ответ: Матрица перевозок: 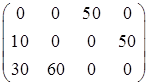. Стоимость перевозок F_min=740 у.е.