Условие интерференционных максимумов и минимумов

Билет № 1

Гармонические колебания- колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид: или

где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд; — полная фаза колебаний, — начальная фаза колебаний.

Фа́за колеба́ний — физическая величина, используемая для описания гармонических или близких к гармоническим колебаний, меняющаяся со временем (чаще всего равномерно растущая со временем), при заданной амплитуде и определяющая состояние колебательной системы в (любой) данный момент времени.

Период колебаний — время (в секундах) между двумя последовательными прохождениями тела через одно и то же положение в одном и том же направлении, величина, обратная частоте.

Период полураспада — время, за которое число ядер данного изотопа уменьшается в два раза.

Чaстота́ — физическая величина, равная числу полных циклов процесса, совершённых за единицу времени. Единицей частоты в Международной системе единиц (СИ) в общем случае является герц (Гц, Hz). Величина, обратная частоте, называется периодом. Частота, как и время, является одной из наиболее точно измеряемых физических величин: до относительной точности 10−17.

Циклическая частота́— скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения, угловая частота равна модулю вектора угловой скорости. В системах СИ и СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны). Угловая частота является производной по времени от фазы колебания:

Начальная фаза, то есть фаза, с которой начинаются колебания.

Ско́рость — векторная физическая величина, характеризующая быстроту перемещения и направления движения материальной точки в пространстве относительно выбранной системы отсчёта (например, угловая скорость). Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.

Ускоре́ние (обозначается а) — производная скорости по времени, векторная величина, показывающая, на сколько изменяется вектор скорости точки (тела) при её (его) движении за единицу времени (то есть ускорение учитывает не только изменение величины скорости, но и её направления). Единицей ускорения служит метр в секунду за секунду (m/s2, м/с2).

Потенциальная энергия U тела, смещенного на расстояние х от положения равновесия, измеряется той работой, которую произведет возвращающая сила, перемещая тело в положение равновесия.

Полная механическая энергия гармонически колеблющегося тела пропорциональна квадрату амплитуды колебания– кинетическая энергия.

Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m. В простейшем случае пружинный маятник представляет собой движущееся по горизонтальной плоскости твердое тело, прикрепленное пружиной к стене. Математи́ческий ма́ятник —осциллятор, представляет собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен и не зависит от амплитуды колебаний и массы маятника. Физический маятник— осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела. Период колебаний пружинного маятникаможет быть вычислен по следующей формуле: , где 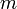— масса груза, — жёсткость пружины. Период колебаний математического маятника: где — длина подвеса (к примеру нити), — ускорение свободного падения.

Период колебаний (на Земле) математического маятника длиной 1 метр с хорошей точностью равен 2 секундам. Период колебаний физического маятника: где — момент инерции маятника относительно оси вращения, 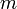— масса маятника, — расстояние от оси вращения до центра масс.

Приведённая длина — это условная характеристика физического маятника. Она численно равна длине математического маятника, период которого равен периоду данного физического маятника. Приведённая длина вычисляется следующим образом:
где I — момент инерции относительно точки подвеса, m — масса, a — расстояние от точки подвеса до центра масс.

Сложение колебаний. Колебания могут складываться и при этом усиливать или гасить друг друга, или изменять траекторию движения тела.

Фигу́ры Лиссажу́ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или вырождаются в отрезки прямых, а при разности фаз и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется.

Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной зависимостью от скорости колебаний или её квадрата.

Вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия. Примеры: листья на деревьях, поднятие и опускание руки. При вынужденных колебаниях может возникнуть явление резонанса:резкое возрастание амплитуды колебаний при совпадении собственной частоты осциллятора и частоты внешнего воздействия.

Свободные (или собственные) — это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие). Простейшими примерами свободных колебаний являются колебания груза, прикреплённого к пружине, или груза, подвешенного на нити.

Билет №2

Волна́— изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве. Другими словами, «…волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой физической величины — например, плотности вещества, напряжённости электрического поля, температуры.

Поперечные электромагнитные волны (радиоволны, свет, рентгеновские лучи), в определённой степени аналог компаундных волн, поскольку образуются переменными во времени диполями, характеристика этих волн распространения в пространстве аналогична акустическим; (волны сдвига, S-волны) — частицы среды колеблются перпендикулярно направлению распространения волны (электромагнитные волны, волны на поверхностях разделения сред);

Продольные ЭМ волны, возникающие при униполярном возбуждении переменным во времени монополем: Схема радиально расположенных диполей (красный цвет соответствует положительному заряду, а синий - отрицательному заряду диполя), волны (волны сжатия, P-волны) — частицы среды колеблются параллельно (по) направлению распространения волны (как, например, в случае распространения звука);

Бегущая волна - волна, которая при распространении в среде переносит энергию (в отличие от стоячей волны). Бегущая волна — волновое возмущение, изменяющееся во времени и пространстве согласно выражению

где — амплитудная огибающая волны, — волновое число и — фаза колебаний.

Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах, обычно длина волны обозначается греческой буквой 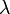. Одна из основных характеристик колебаний. Измеряется в единицах расстояния (метры, сантиметры и т. п.).

Когерентностью называется согласованность нескольких колебательных или волновых процессов во времени, проявляющаяся при их сложении. Колебания когерентны, если разность их фаз постоянна во времени и при сложении колебаний получается колебание той же частоты.

Интерференция — изменение в характере звуковых, тепловых, световых и электрических явлений, объясняемое колебательным движением: в первом случае частиц звучащего тела, в остальных трех — колебанием. Интерференция света — частный случай интерференции для видимой области электромагнитного спектра;Интерференция света — перераспределение интенсивности света в результате наложения (суперпозиции) нескольких световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной. — условие максимума;

— условие минимума, где k=0,1,2... и — оптическая длина пути первого и второго луча, соответственно.

Стоя́чая волна́ — колебания в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения.

Билет № 3

Молекулярная физика — раздел физики, который изучает физические свойства тел на основе рассмотрения их молекулярного строения. Задачи молекулярной физики решаются методами физической статистики, термодинамики и физической кинетики, они связаны с изучением движения и взаимодействия частиц (атомов, молекул, ионов), составляющих физические тела.

Молекулярно-кинетическая теория (сокращённо МКТ) — теория XIX века, рассматривавшая строение вещества, в основном газов, с точки зрения трёх основных приближенно верных положений:

1) все тела состоят из частиц: атомов, молекул и ионов;

2) частицы находятся в непрерывном хаотическом движении (тепловом);

3) частицы взаимодействуют друг с другом путём абсолютно упругих столкновений.

Основными доказательствами этих положений считались: диффузия, Броуновское движение, изменение агрегатных состояний вещества

Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.

Основное уравнение МКТ , где k - является постоянной Больцмана (отношение универсальной газовой постоянной R к числу Авогадро N_A), i — число степеней свободы молекул ( в большинстве задач про идеальные газы, где молекулы предполагаются сферами малого радиуса, физическим аналогом которых могут служить инертные газы), а T - абсолютная температура. Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) газовой системы с микроскопическими (масса молекул, средняя скорость их движения).

Понятие абсолютной температуры было введено У. Томсоном (Кельвином), в связи с чем шкалу абсолютной температуры называют шкалой Кельвина или термодинамической температурной шкалой. Единица абсолютной температуры — кельвин (К). Абсолютная шкала температуры называется так, потому что мера основного состояния нижнего предела температуры — абсолютный ноль, то есть наиболее низкая возможная температура, при которой в принципе невозможно извлечь из вещества тепловую энергию. Абсолютный ноль определён как 0 K, что равно −273.15 °C. Шкала температур Кельвина — это шкала, в которой начало отсчёта ведётся от абсолютного нуля.

Сте́пени свобо́ды — характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных (обобщённых координат), необходимых для полного описания движения механической системы.

Число степеней свободы. Формула внутренней энергии газа:

,и прямо связанная с ней формула для средней энергии молекулы газа

, где — количество степеней свободы молекулы газа, — количество газа ( 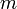— масса, — молярная масса газа), 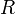— универсальная газовая постоянная, — константа Больцмана,

— абсолютная температура газа.

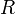Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид: где — давление, — молярный объём, — универсальная газовая постоянная — абсолютная температура,К.

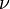Так как , где — количество вещества, а , где 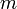— масса, — молярная масса, уравнение состояния можно записать: Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.

Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:

— закон Бойля — Мариотта.

— Закон Гей-Люссака.

— закон Шарля (второй закон Гей-Люссака, 1808 г.)

Законы Дальтона — два физических закона, определяющих суммарное давление и растворимость смеси газов. Сформулированы Джоном Дальтоном в начале XIX века^. Закон о суммарном давлении смеси газов: Давление смеси химически не взаимодействующих идеальных газов равно сумме парциальных давлений.

Закон о растворимости компонентов газовой смеси:При постоянной температуре растворимость в данной жидкости каждого из компонентов газовой смеси, находящейся над жидкостью, пропорциональна их парциальному давлению.

Закон Авога́дро — одно из важных основных положений химии, гласящее, что «в равных объёмах различных газов, взятых при одинаковых температуре и давлении, содержится одно и то же число молекул». Было сформулировано ещё в 1811 году Амедео Авогадро (1776—1856).

Первое следствие из закона Авогадро: один моль любого газа при одинаковых условиях занимает одинаковый объём. В частности, при нормальных условиях, бъём 1 моля газа, равен 22,4 л. Этот объём называют молярным объёмом газа V_m. Пересчитать эту величину на другие температуру и давление можно с помощью уравнения Менделеева-Клапейрона:

.

Второе следствие из закона Авогадро: молярная масса первого газа равна произведению молярной массы второго газа на относительную плотность первого газа по второму.

Билет № 4

Вну́тренняя эне́ргия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии: где — подведённая к телу теплота, измеренная в джоулях, — работа, совершаемая телом против внешних сил, измеренная в джоулях

Механическая работа— физическая величина, зависящая от векторов силы и перемещения. Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек) тела или системы

Теплота́ сгора́ния — это количество выделившейся теплоты при полном сгорании массовой (для твердых и жидких веществ) или объёмной (для газообразных) единицы вещества. Измеряется в джоулях или калориях. Теплота сгорания, отнесённая к единице массы или объёма топлива, называется удельной теплотой сгорания (дж или кал на 1 кг, м³ или моль).

Теплоемкость идеального газа — это отношение количества теплоты, сообщенного газу, к изменению температуры δТ, которое при этом произошло. . Теплоемкость идеального газа бывает: адиабатической, изотермической, изохорной, изобарной

Молярная теплоёмкость — это теплоёмкость одного моля вещества. Часто употребляется обозначение .Связь с удельной теплоёмкостью: , где c — удельная теплоёмкость, μ — молярная масса. Размерность молярной теплоёмкости [Дж/(К•моль)]

Уде́льная теплоёмкость вещества определяется как количество тепловой энергии, необходимой для повышения температуры одного килограмма вещества на один градус. Единицей СИ для удельной теплоёмкости является джоуль на килограмм-кельвин. Следовательно, удельную теплоёмкость можно рассматривать как теплоёмкость единицы массы вещества. Формула расчёта удельной теплоёмкости: , где — удельная теплоёмкость, — количество теплоты, полученное веществом при нагреве (или выделившееся при охлаждении), 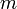— масса нагреваемого (охлаждающегося) вещества, — разность конечной и начальной температур вещества.

Показатель адиабаты (иногда называемый коэффициентом Пуассона) — отношение теплоёмкости при постоянном давлении ( ) к теплоёмкости при постоянном объёме ( ). Обозначается греческой буквой (гамма) или (каппа). Уравнение: , где — теплоёмкость газа, — удельная теплоёмкость (отношение теплоёмкости к единице массы) газа, индексы и обозначают условие постоянства давления или постоянства объёма.

Первое начало термодинамики — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии для термодинамических систем.1.В любой изолированной системе запас энергии остаётся постоянным. Формулировка Дж. П. Джоуля (1842 г.). 2.Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил 3.Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе, то есть, оно зависит только от начального и конечного состояния системы и не зависит от способа, которым осуществляется этот переход. Иными словами, внутренняя энергия является функцией состояния. В циклическом процессе внутренняя энергия не изменяется.

4. Изменение полной энергии системы в квазистатическом процессе равно количеству теплоты , сообщённому системе, в сумме с изменением энергии, связанной с количеством вещества 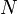при химическом потенциале , и работы , совершённой над системой внешними силами и полями, за вычетом работы 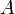, совершённой самой системой против внешних сил

.

В адиабатическом процессе теплообмена с окружающей средой не происходит, то есть . Однако, объём, давление и температура меняются, то есть .Следовательно, теплоемкость идеального газа в адиабатическом процессе равна нулю: . В изотермическом процессе постоянна температура, то есть . При изменении объема газу передается (или отбирается) некоторое количество тепла. Следовательно, теплоемкость идеального газа стремится к бесконечности: . В изохорном процессе постоянен объем, то есть . Элементарная работа газа равна произведению изменения объема на давление, при котором происходит изменение ( ). Первое Начало Термодинамики для изохорного процесса имеет вид: . А для идеального газа

В изобарном процессе ( )

Билет № 5

Адиабати́ческий, или адиаба́тный проце́сс — термодинамический процесс в макроскопической системе, при котором система не обменивается тепловой энергией с окружающим пространством. При Адиабатический процессе теплоёмкость газа равна нулю и, постоянна. Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётся равновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит.

Уравнение адиабатического процесса. Если термодинамический процесс в общем случае являет собой три процесса — теплообмен, совершение системой (или над системой) работы и изменение её внутренней энергии, то адиабатический процесс в силу отсутствия теплообмена ( ) системы со средой сводится только к последним двум процессам. Поэтому, первое начало термодинамики в этом случае приобретает вид где — изменение внутренней энергии тела, 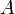— работа, совершаемая системой. Изменения энтропии S системы в обратимом адиабатическом процессе вследствие передачи тепла через границы системы не происходит: Здесь — температура системы, — теплота, полученная системой. Благодаря этому адиабатический процесс может быть составной частью обратимого цикла

Показатель адиабаты (называемый коэффициентом Пуассона) — отношение теплоёмкости при постоянном давлении ( ) к теплоёмкости при постоянном объёме ( ). Иногда его ещё называют фактором изоэнтропийного расширения. Обозначается греческой буквой (гамма) или (каппа). Буквенный символ в основном используется в химических инженерных дисциплинах. В теплотехнике используется латинская буква . Уравнение: , где — теплоёмкость газа, — удельная теплоёмкость (отношение теплоёмкости к единице массы) газа, индексы и обозначают условие постоянства давления или постоянства объёма, соответственно.

Работа в адиабатическом процессе. когда работа совершается через изменение объёма, можно определить её следующим способом: пусть газ заключён в цилиндрический сосуд, плотно закрытый легко скользящим поршнем, если газ будет расширяться, то он будет перемещать поршень и при перемещении на отрезок совершать работу где F — сила, с которой газ действует на поршень. Перепишем уравнение: где s — площадь поршня. Тогда работа будет равна где — давление газа, — малое приращение объёма. Основное уравнение термодинамики примет вид: скорость должна быть достаточно большой, чтобы можно было пренебречь обменом тепла с окружающей средой и процесс оставался адиабатическим.

Теплова́я маши́на — устройство, преобразующее тепловую энергию в механическую работу (тепловой двигатель) или механическую работу в тепло (холодильник). Принцип работы тепловой машины: преобразование осуществляется за счёт изменения внутренней энергии рабочего тела — на практике обычно пара или газа. Идеальная тепловая машина — машина, в которой произведённая работа и разница между количеством подведённого и отведённого тепла равны. Работа идеальной тепловой машины описывается циклом Карно. При работе часть тепла Q1 передается от нагревателя к рабочему телу, а затем часть энергии Q2 передается холодильнику, который охлаждает машину. КПД тепловой машины считается по формуле (Q1-Q2/Q1)х100.Периодически действующий двигатель, совершающий работу за счет получаемого извне тепла, называется тепловой машиной.

Цикл Карно́ — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно. Состоит из 2 адиабатических и 2 изотермических процессов. Одним из важных свойств цикла Карно является его обратимость: он может быть проведён как в прямом, так и в обратном направлении, при этом энтропия адиабатически изолированной системы не меняется. Цикл Карно состоит из четырёх стадий: Изотермическое расширение, Адиабатическое расширение, Изотермическое сжатие, Адиабатическое сжатие

КПД цикла Карно. Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно . Аналогично, при изотермическом сжатии рабочее тело отдало холодильнику

. Отсюда коэффициент полезного действия тепловой машины Карно равен

. КПД тепловой машины Карно зависит только от температур нагревателя и холодильника. КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Поэтому максимальный КПД любой тепловой машины будет меньше или равен КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника.

Билет № 6

Геометри́ческая о́птика — раздел оптики, изучающий законы распространения света в прозрачных средах и принципы построения изображений при прохождении света в оптических системах без учёта его волновых свойств.

В основе геометрической оптики лежат несколько простых эмпирических законов: 1) Закон прямолинейного распространения света 2) Закон независимого распространения лучей 3) Закон отражения света 4) Закон преломления света (Закон Снелла) 5) Закон обратимости светового луча. Согласно нему луч света, распространившийся по определённой траектории в одном направлении, повторит свой ход в точности при распространении и в обратном направлении.

Вну́треннее отраже́ние — явление отражения электромагнитных или звуковых волн от границы раздела двух сред при условии, что волна падает из среды, где скорость ее распространения меньше (в случае световых лучей это соответствует бо́льшему показателю преломления). Полное внутреннее отражение — внутреннее отражение, при условии, что угол падения превосходит некоторый критический угол. При этом падающая волна отражается полностью, и значение коэффициента отражения превосходит его самые большие значения для полированных поверхностей. Коэффициент отражения при полном внутреннем отражении не зависит от длины волны.

Мираж— оптическое явление в атмосфере: отражение света границей между резко различными по плотности слоями воздуха. Для наблюдателя такое отражение заключается в том, что вместе с отдалённым объектом (или участком неба) видно его мнимое изображение, смещённое относительно предмета. Миражи делят на нижние, видимые под объектом, верхние, — над объектом, и боковые.

Диспе́рсия све́та (разложение света) — это явление, обусловленное зависимостью абсолютного показателя преломления вещества от частоты (или длины волны) света (частотная дисперсия), или, то же самое, зависимость фазовой скорости света в веществе от длины волны (или частоты).. Пространственной дисперсией называется зависимость тензора диэлектрической проницаемости среды от волнового вектора. Такая зависимость вызывает ряд явлений, называемых эффектами пространственной поляризации.

Ра́дуга — атмосферное оптическое и метеорологическое явление, наблюдаемое при освещении Солнцем (иногда Луной) множества водяных капель (дождя или тумана). Радуга выглядит как разноцветная дуга или окружность, составленная из цветов спектра (от внешнего края внутрь: красный, оранжевый, жёлтый, зелёный, голубой, синий, фиолетовый). Это те семь цветов, которые принято выделять в радуге в русской культуре (возможно, вслед за Ньютоном, см. ниже), но следует иметь в виду, что на самом деле спектр непрерывен, и его цвета плавно переходят друг в друга через множество промежуточных оттенков. Центр окружности, описываемой радугой, лежит на прямой, проходящей через наблюдателя и Солнце, притом при наблюдении радуги Солнце всегда находится за спиной наблюдателя, и одновременно видеть Солнце и радугу без использования оптических приспособлений невозможно.

Интерференция света — перераспределение интенсивности света в результате наложения (суперпозиции) нескольких световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной.