Решение четырех основных задач способом замены плоскостей проекций

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ВЫПОЛНЕНИЮ РАБОТЫ № 2

Москва-2008

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ (МИИТ)

Институт пути, строительства и сооружений

Кафедра «Начертательная геометрия и черчение»

Н.П. ГОРБАЧЕВА

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ

Рекомендовано редакционно-издательским советом университета в качестве методических указаний для студентов ИПСС

Москва-2008

УДК 513

Г 67

Горбачева Нина Петровна. Начертательная геометрия. -М.: МИИТ, 2008.- 21с.

Настоящие методические указания составлены с целью оказания помощи студентам в процессе выполнения домашней работы №2 по начертательной геометрии по теме «Преобразование эпюра».

© Московский государственный университет путей сообщения (МИИТ), 2008

ВВЕДЕНИЕ

Работа № 2 по дисциплине «Начертательная геометрия» содержит метрические и позиционные задачи, решение которых значительно упрощается, когда рассматриваемые геометрические фигуры имеют частное положение. Так, например, если прямая параллельна плоскости проекций, то легко определяется ее натуральная величина. Так же легко определить проекции точки пересечения прямой с плоскостью частного положения и т.д. Возникает необходимость в создании таких приемов, которые позволили бы переводить фигуры из общего по отношению к плоскостям проекций положения в частное. С этой целью используют способ замены плоскостей проекций.

СПОСОБ ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ

Сущность способа замены плоскостей проекций заключается в том, что одна из основных плоскостей проекций заменяется новой плоскостью, перпендикулярной незаменяемой. Положение самого объекта в пространстве при этом останется неизменным. Последовательное введение новых плоскостей проекций дает

возможность получить такую новую систему плоскостей, относительно которой геометрический элемент займет частное положение.

ОСНОВЫ СПОСОБА

Основы способа замены плоскостей проекций заключаются в следующем:

1. Положение рассматриваемой геометрической фигуры в пространстве не изменяется по отношению к исходной «старой» системе плоскостей проекций.

2. «Новая» система взаимно перпендикулярных плоскостей выбирается так, чтобы рассматриваемая геометрическая фигура оказалась бы в частном положении по отношению к одной из плоскостей новой системы.

3. Построенная на такой плоскости ортогональная проекция геометрической фигуры является искомой вспомогательной проекцией этой фигуры.

В некоторых случаях достаточно заменить только одну плоскость старой системы, в неко-

торых – необходима последовательная замена обеих плоскостей

На рис. 1 показана точка A, заданная в системе плоскостей П₂/П₁.

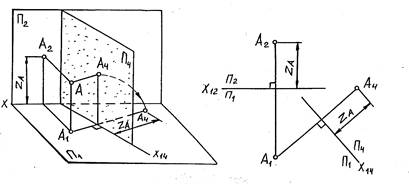Рис. 1 Рис. 2

Заменим плоскость П₂ новой фронтальной плоскостью П₄, перпендикулярной к П₁. Построим новую фронтальную проекцию точки на эту плоскость. Так как горизонтальная плоскость проекции П₁ является общей для «старой» и «новой» систем, координата Z точки А остается неизменной. Следовательно, расстояние от новой фронтальной проекции до новой оси X₁₄ равно координате Z старой системы. При этом горизонтальная проекция

точки A остается прежней, а координата Y точки будет равна расстоянию от точки A до плоскости П₄. Для получения эпюра плоскость П₄ вращением вокруг оси X₁₄ совмещается с П₁. При этом A₄ окажется на общем перпендикуляре к новой оси X₁₄ (рис.2).

Аналогично можно заменить горизонтальную плоскость проекций П₁ плоскостью П₅ (рис. 3). В этом случае общей плоскостью для обеих систем является плоскость П₂. При построении «новой» горизонтальной проекции точки от оси X₂₅ отложена Y_A взятая в системе П₂/П₁.

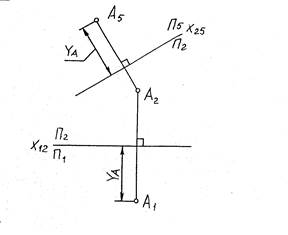
Рис. 3

РЕШЕНИЕ ЧЕТЫРЕХ ОСНОВНЫХ ЗАДАЧ СПОСОБОМ ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ