Постановка задачи линейного программирования

Задачей линейного программирования (ЗЛП) в нормальной форме называется задача максимизации (минимизации) целевой функции

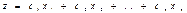(1)

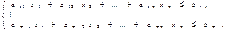
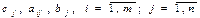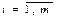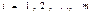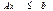
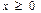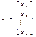
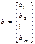
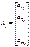
по переменным удовлетворяющим неравенствам , где постоянные числа. Запись означает, что .В матричной форме задача имеет вид , (4) , , 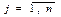, 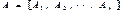. x называется вектором-переменной, 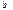− вектор ограничений, c − вектор стоимости, 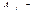векторы условий, 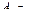матрица условий, символ 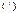означает транспонирование.Наряду с нормальной формой задачи линейного программирования (4)−(6), широкое распространение получила каноническая форма, под которой понимается следующая задача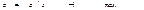 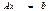, 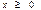где все компоненты вектора x неотрицательны.Две формы ЗЛП отличаются лишь типом ограничений. В нормальной форме ограничения типа неравенств, в канонической − типа равенств. Ограничения типа неравенств можно свести введением неотрицательных свободных переменных к ограничениям типа равенств. В первое неравенство ограничений (2) добавим свободную переменную 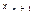, второе − 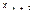, последнее − 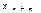. Коэффициенты 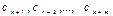, соответствующие свободным переменным, равны нулю.

Одним из основных аналитических методов решения ЗЛП является симплекс-метод[6-8]. Теория и алгоритм симплекс-метода строится только для канонической формы (7) − (9) ЗЛП.

Планом или допустимым решением ЗЛП называется вектор 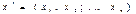, удовлетворяющий системе ограничений (8)-(9). План задачи (7)−(9), для которого линейная форма достигает максимума, называется оптимальным. План называется базисным (опорным), если вектора условий 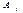соответствующие

ненулевым компонентам, линейно независимы. Базисный план называется невырожденным, если он содержит ровно m положительных компонент.

Решение ЗЛП состоит из трех основных этапов: 1) построение первоначального невырожденного базисного плана; 2) проверка плана на оптимальность; 3) в случае неоптимальности плана указание процедуры перехода к новому плану.

2 этап. Критерий оптимальности базисного плана. Критерием оптимальности рассматриваемого решения (плана) является выполнение условия 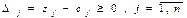.Если это условие не выполняется для некоторого номера j и все элементы 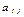этого столбца неположительные, то целевая функция не ограничена на множестве допустимых планов. Если же существуют столбцы с 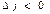, но в каждом из них имеются положительные элементы 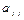тогда следует искать новый план, при котором значение функции z было бы больше. Для этого переходим к новому базису. Чтобы определить, какой вектор следует ввести в базис, просматривают последнюю строку. Вектор, соответствующий минимальному отрицательному 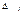, вводится в базис (если имеется несколько таких одинаковых 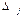, то берется любой). Пуст 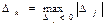, тогда вектор 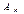нужно ввести в базис. Столбец, содержащий число 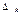, называется разрешающим столбцом симплексной таблицы. Чтобы определить, какой вектор нужно вывести из базиса, вычисляют минимальное отношение координат 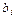вектора 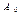к положительным элементам 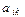разрешающего столбца, т. е. находятся симплексные отношени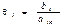я для 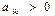и помещают их в столбец 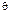, затем среди них выбирают наименьшее − 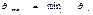. Пусть 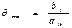, тогда вектор 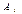нужно исключить из базиса. В симплексной таблице строка, содержащая число 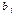, называется разрешающей, а элемент 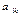, стоящий на пересечении разрешающих столбца и строки, − разрешающим (ключевым) элементом.

Разрешающие строка и столбец в симплексной таблице (табл. 1) выделяются двойными линиями и отмечаются стрелками.

3 этап. Переход к новому базисному плану. После того, как определены разрешающие строка и столбец, строится новая симплексная таблица. В первом столбце записывается новый базис. Он отличается от старого одним вектором: вместо вектора 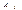в базис вводится вектор 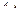. Соответственно заменяется коэффициент 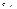коэффициентом 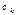в столбце .

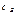Новые координаты векторов 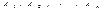находим по формулам: 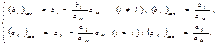При построении новой симплекс-таблицы рекомендуются следующие правила: 1) элементы разрешающей строки, начиная со столбца b, делятся на разрешающий элемент; 2) вместо элементов разрешающего столбца, кроме разрешающего элемента, пишутся нули, а на месте разрешающего элемента − единица; 3) все остальные элементы 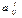, начиная со столбца b, находятся по правилу “прямоугольника” (Рис.1). В первоначальной таблице строят прямоугольник с вершинами в разрешающем элементе, на разрешающей строке и на разрешающем столбце, т. е. 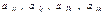Перемножаем элементы 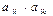, не лежащие на одной диагонали с 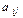, делим результат на 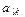и полученное число вычитаем из 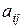. В результате получаем новое значение 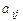. Аналогично вычисляются и значения 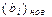. 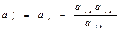Новую симплекс-таблицу можно также строить по правилу “сложения строк”. В этом случае рекомендуются следующие правила заполнения симплекс-таблицы: 1) элементы разрешающей строки, начиная со столбца b, делятся на разрешающий элемент; 2) умножением элементов разрешающей строки на 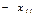(i-й элемент разрешающего столбца, умноженный на минус единицу) и сложением с соответствующими элементами i-й строки получают i-ю строку новой симплекс-таблицы, при этом разрешающий столбец становится единичным (1 на месте разрешающего элемента, нули − на остальных местах). После заполнения новой симплекс-таблицы проверяем план 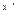на оптимальность. Если при решении задачи на максимум в новой таблице все оценки 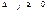, то план 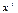является оптимальным; если же хотя бы одна из разностей 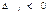, то нужно строить новую симплексную таблицу по тем же правилам. Процесс продолжается до тех пор, пока не будет получен оптимальный план, т. е. пока не станут положительными все оценки, 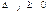. Все отличные от нуля координаты вектора 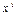находятся в столбце вектора b, номер (индекс) координаты совпадает с номером базисного вектора, стоящего в той же строке, что и сама координата.

Поток событий. Основные понятия и характеристики

Потоком событийназывается последовательность событий, происходящих один за другим в какие- то моменты времени.

Характер событий, образующих поток может быть различным, а если события отличаются друг от друга только моментом времени, в который они происходят, то такой поток событий называется однородным.

Однородный поток можно изобразить последовательностью точек на оси, соответствующей времени:

Поток событий называется регулярным, если события следует одно за другим через строго определенные промежутки времени.

Поток событий называется стационарным, если вероятность попадания того ли иного числа событий на участок времени t зависит только от длины участка и не зависит от того, где именно на оси расположен этот участок.

Стационарность потока событий означает, что плотность потока постоянна, отсутствуют промежутки времени, в течение которых событий больше чем обычно. Классический пример – “час пик” на транспорте.

Поток событий называется потоком без последействий, если для любых неперекрещивающихся участков времени число событий, попадающих на один из них, не зависит от числа событий, опадающих на другие.

Поток событий называется ординарным, если вероятность попадания на элементарный участок Dt двух или более событий достаточно мало по сравнению с вероятностью попадания одного события.

Условие ординарности означает, что заявки на систему приходят по одному, а не парами, тройками и т.д. Однако, если заявки поступают только парами, только тройками и т.д., то такой поток легко свести к ординарному.

Если поток событий стационарен, ординарен и без последействий, то такой поток называется простейшим (пуассоновским)потоком.

Это название связано с тем, что в этом случае число событий, попадающих на любой фиксированный интервал времени, распределено по распределению Пуассона .

В соответствии с этим законом распределения математическое ожидание числа точек, попавших попадающих на участок времени t, имеет вид:

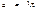l - плотность потока – среднее число событий в единицу времени.

Вероятность того, что за время t произойдет ровно т событий, равна

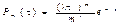
Вероятность того, что в течение данного времени не произойдет ни одного события, равна:

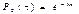
Пусть Т – промежуток времени между двумя произвольными соседними событиями в простейшем потоке. Найдем функцию распределения

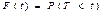
В соответствии с законом распределения Пуассона, получаем:

Математическое ожидание, дисперсия и среднее квадратическое отклонение этой величины соответственно равны:

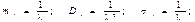
Марковские прочесы.

Определение. Процесс, протекающий в физической системе, называется марковским, если в любой момент времени вероятность любого состояния системы в будущем зависит только от состояния системы в текущий момент и не зависит от того, каким образом система пришла в это состояние.

Определение. Цепью Маркова называется последовательность испытаний, в каждом из которых появляется только одно из k несовместных событий A_i из полной группы. При этом условная вероятность p_ij(s) того, что в s –ом испытании наступит событие A_j при условии, что в (s – 1) – ом испытании наступило событие A_i, не зависит от результатов предшествующих испытаний.

Независимые испытания являются частным случаем цепи Маркова. События называются состояниями системы, а испытания – изменениями состояний системы.

По характеру изменений состояний цепи Маркова можно разделить на две группы.

Определение. Цепью Маркова с дискретным временемназывается цепь, изменение состояний которой происходит в определенные фиксированные моменты времени. Цепью Маркова с непрерывным временемназывается цепь, изменение состояний которой возможно в любые случайные моменты времени.

Определение. Однороднойназывается цепь Маркова, если условная вероятность p_ij перехода системы из состояния i в состояние j не зависит от номера испытания. Вероятность p_ij называется переходной вероятностью.

Допустим, число состояний конечно и равно k.

Тогда матрица, составленная из условных вероятностей перехода будет иметь вид:

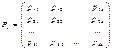
Эта матрица называется матрицей перехода системы.

Т.к. в каждой строке содержаться вероятности событий, которые образуют полную группу, то, очевидно, что сумма элементов каждой строки матрицы равна единице.

На основе матрицы перехода системы можно построить так называемый граф состояний системы,его еще называют размеченный граф состояний. Это удобно для наглядного представления цепи. Порядок построения граф рассмотрим на примере.

Пусть P_ij(n) – вероятность того, что в результате n испытаний система перейдет из состояния i в состояние j, r – некоторое промежуточное состояние между состояниями i и j. Вероятности перехода из одного состояния в другое p_ij(1) = p_ij.

Тогда вероятность P_ij(n) может быть найдена по формуле, называемой равенством Маркова:

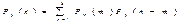
Здесь т – число шагов (испытаний), за которое система перешла из состояния i в состояние r.

В принципе, равенство Маркова есть ни что иное как несколько видоизменная формула полной вероятности.

Зная переходные вероятности (т.е. зная матрицу перехода Р₁), можно найти вероятности перехода из состояния в состояние за два шага P_ij(2), т.е. матрицу Р₂, зная ее – найти матрицу Р₃, и т.д.

Непосредственное применений полученной выше формулы не очень удобно, поэтому, можно воспользоваться приемами матричного исчисления (ведь эта формула по сути – не что иное как формула перемножения двух матриц).

Тогда в общем виде можно записать: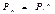

Вообще то этот факт обычно формулируется в виде теоремы, однако, ее доказательство достаточно простое, поэтому приводить его не буду.

Финальные вероятности

Теорема. (теорема о предельных вероятностях) Пусть дана регулярная цепь Маркова с п состояниями и Р – ее матрица вероятностей перехода. Тогда существует предел 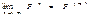и матрица Р^(¥) имеет вид: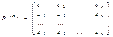

Т.е. матрица состоит из одинаковых строк.

Теперь о величинах u_i. Числа u₁, u₂, …, u_n называются предельными вероятностями.Эти вероятности не зависят от исходного состояния системы и являются компонентами собственного вектора матрицы Р^Т (транспонированной к матрице Р).

Этот вектор полностью определяется из условий:

Пример. Найдем предельные вероятности для рассмотренного выше примера.

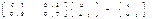
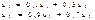
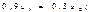
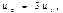C учетом того, что u₁ + u₂ = 1, получаем:

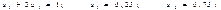Получаем: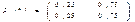

Процесс гибели – размножения и циклический процесс.

Определение. Марковский процесс с дискретными состояниями называют процессом гибели – размножения, если он имеет размеченный граф состояний следующего вида:

Т.е. каждое из состояний системы связано с двумя соседними состояниями прямой и обратной связью, крайние состояния имеют только по одному соседнему.

Здесь l_ij – плотность вероятности перехода системы из состояния S_i в состояние S_j в момент времени t.

Эта плотность находится по формуле:

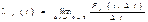
Dt – время перехода из одного состояния в другое.

Изменив знак целвой функции (1) от ЗЛП на max можно перейти к задаче на min и наоборот.шзшзш

лица 2