Тема 8. Исследование функций

Тема 1. Матрицы и определители

1. Вычислить определитель.

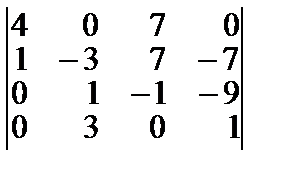
Решение:

Вычислим определитель 4 порядка с помощью разложения по первому столбцу.

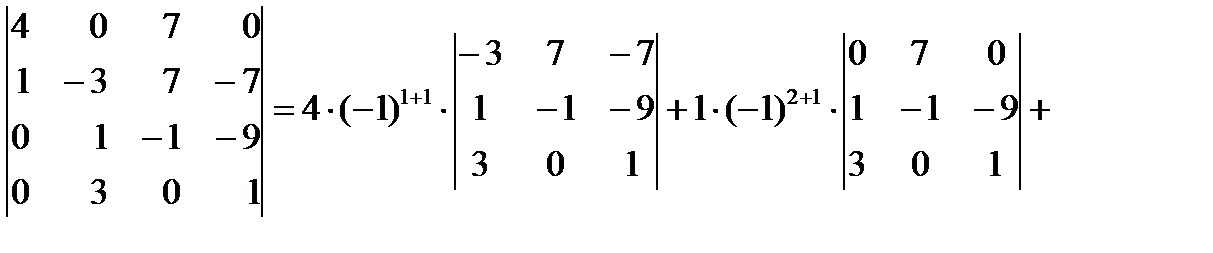
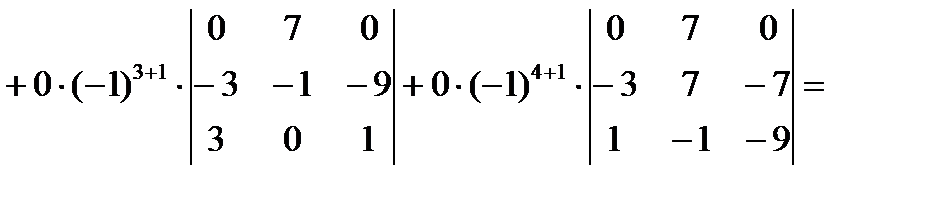
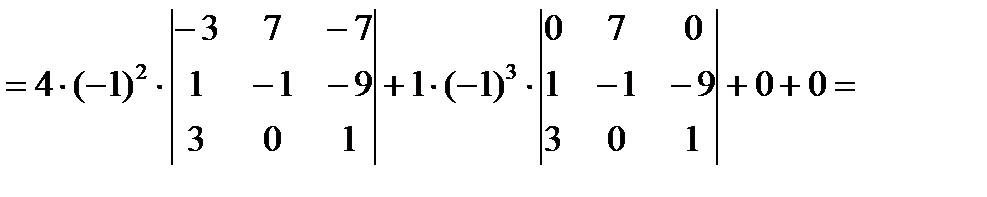
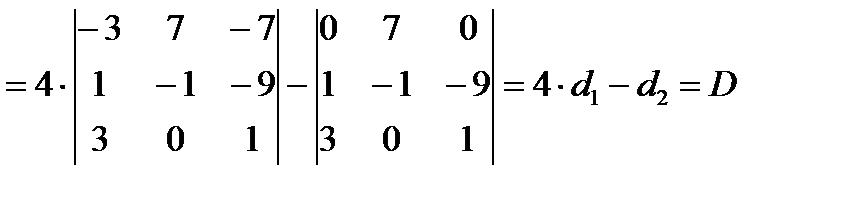
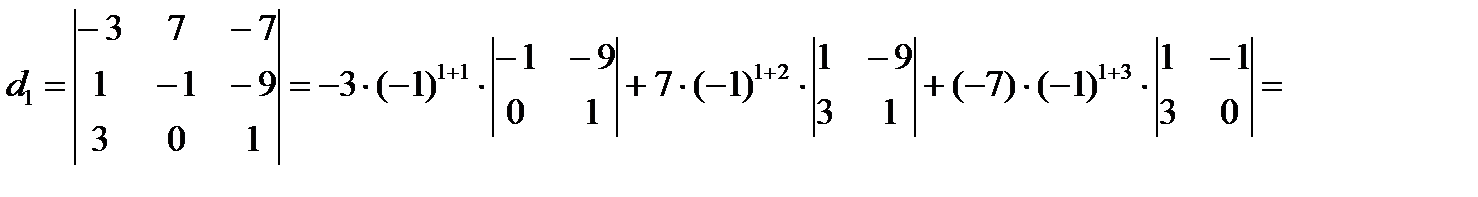
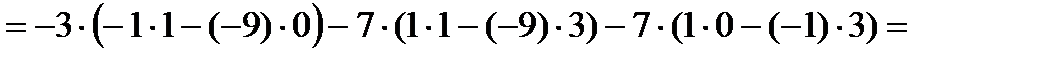
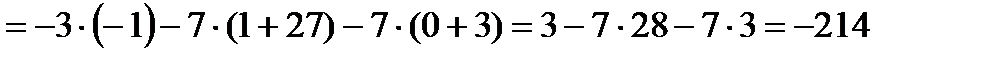
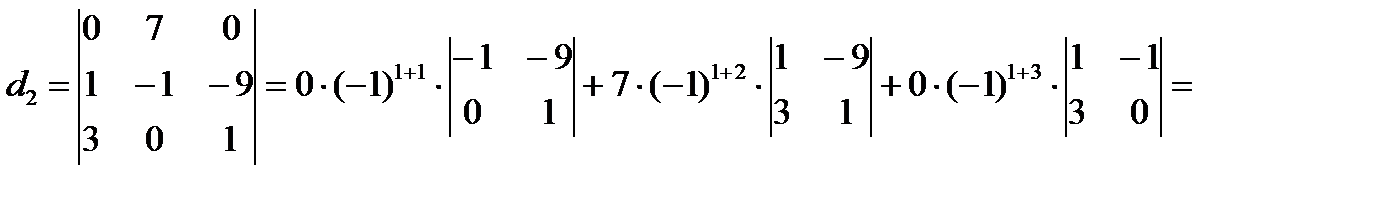
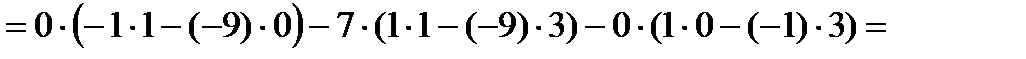
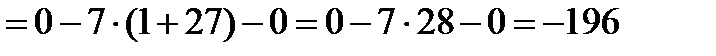
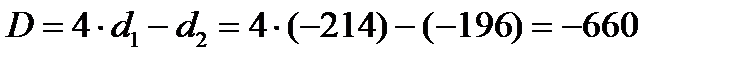
Ответ: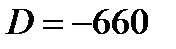

1.2. Найти обратную матрицу для матрицыА и сделать проверку.

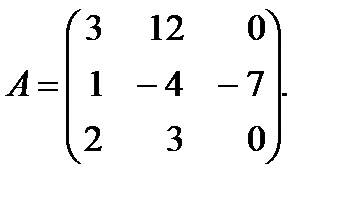
Решение:

Найдем обратную матрицу с помощью миноров.

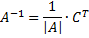
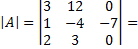
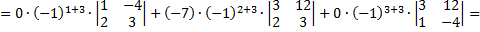
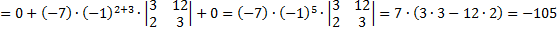
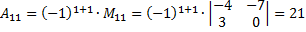
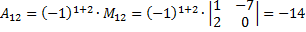
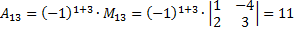
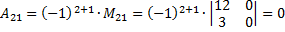
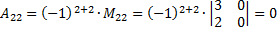
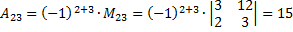
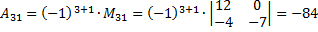
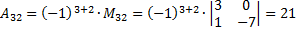
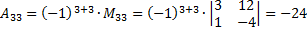
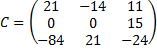
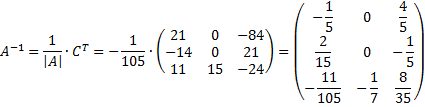
Проверим.

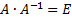
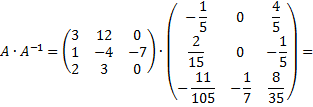
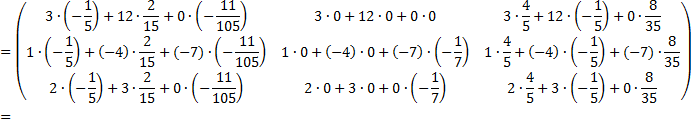
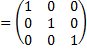
Значит, обратная матрица найдена верно.

Тема 2. Системы линейных уравнений

Решить систему уравнений тремя способами: методом обратной матрицы, методом Гаусса или методом Жордана–Гаусса.

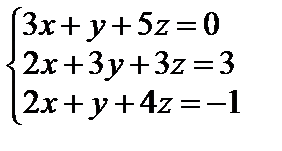
Решение:

Решим методом Гаусса.

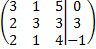
Из третьей строки вычтем вторую.

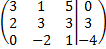
Разделим вторую строку на 2. Разделим первую строку на 3.

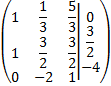
Из второй строки вычтем первую:

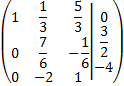
Умножим вторую строку на

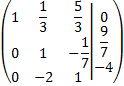
К третьей строке прибавим вторую, умноженную на 2.

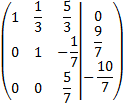
Получили:

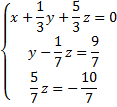
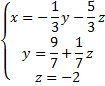
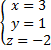
Ответ: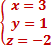

Тема 4. Уравнение плоскости

Даны точки М₁ и М₂.

Составить уравнение плоскости, проходящей через точку ш₁ перпендикулярно вектору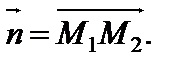

Найти отрезки, отсекаемые данной плоскостью на осях координат. Начертить эту плоскость.

Составить уравнение плоскости, проходящей через точку ш₁ перпендикулярно вектору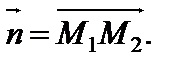

Найти отрезки, отсекаемые данной плоскостью на осях координат. Начертить эту плоскость.

7. М₁(3; 2; –2); М₂(5; 1; 2).

Решение:

Составим уравнение вектора нормали:

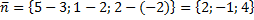
Уравнение плоскости с помощью нормального вектора записывается в виде:

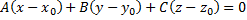
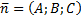
Значит,

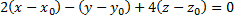
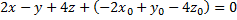уравнение плоскости.

Тема 3–4. Векторная алгебра. Уравнение прямой

По координатам вершин треугольника ABC найти: периметр треугольника; уравнения сторон AB и BC; уравнение высоты AD; угол ABC; площадь треугольника. Сделать чертеж.

7. А(–1; 4) В(–1; 2); С(–7; 3).

Решение:

Чертеж:

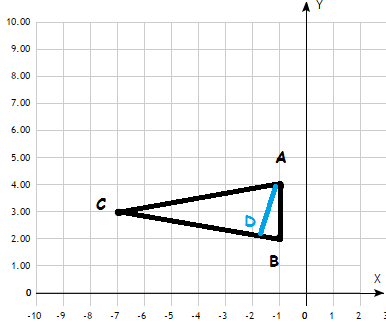
Уравнение сторон:

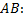
А(–1; 4) В(–1; 2)

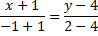
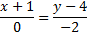
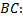
В(–1; 2); С(–7; 3)

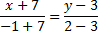
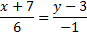
Уравнение высоты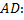

Нужно найти прямую, проходящую через точку 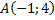и перпендикулярно прямой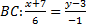

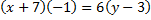
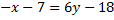
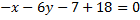
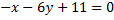
Значит, нормальный вектор для 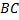совпадает с направляющим вектором высоты.

Значит,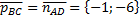

Значит,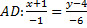

Тема 5. Линии второго порядка

Составьте уравнение окружности с центром в заданной точкеА и данным радиусом R. Сделать чертеж.

Уравнение окружности имеет вид: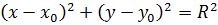
1. А(1; –7); R = 1.

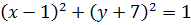
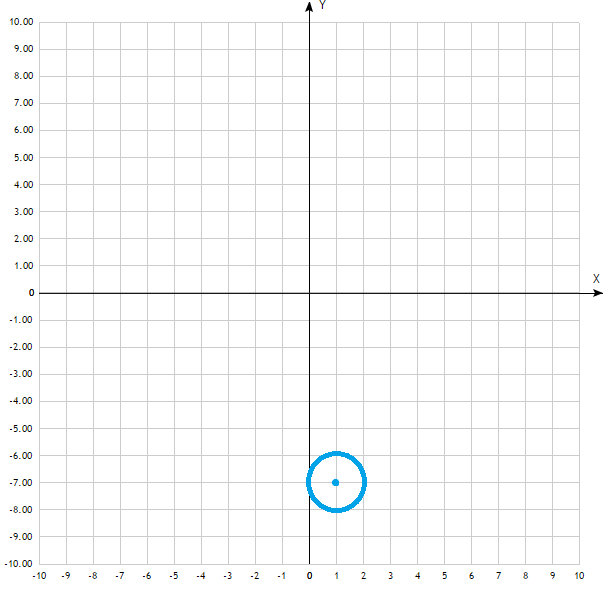
2. А(–2; 6); R = 2.

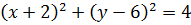
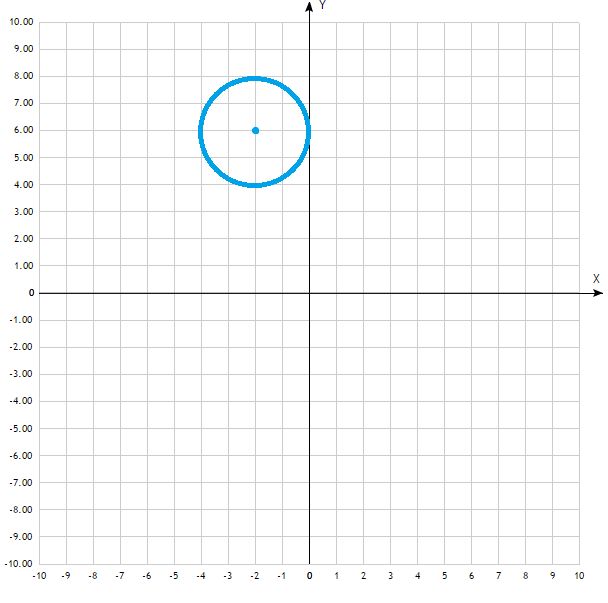
3. А(–3; 2); R = 3.

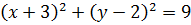
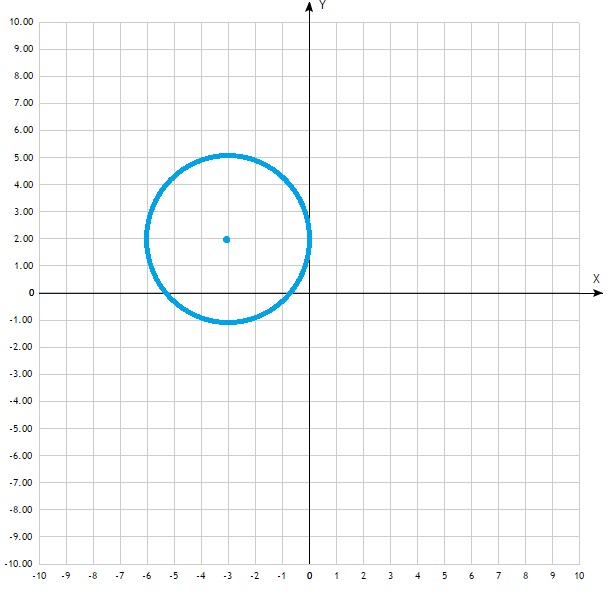
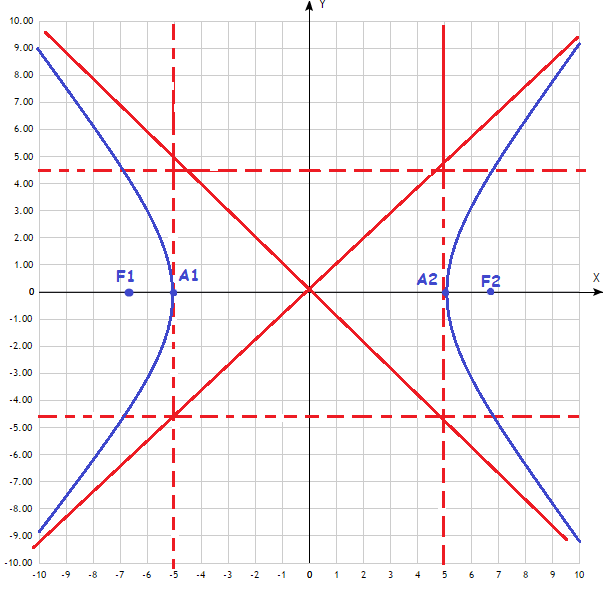
По заданному уравнению гиперболы найти: координаты вершин, координаты фокусов, эксцентриситет, уравнение асимптот. Сделать чертеж.

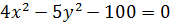
Приведем к каноническому виду:

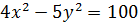
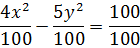
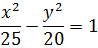
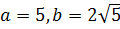
Координаты вершин: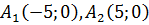

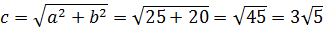
Координаты фокусов: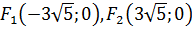

Эксцентриситет: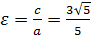

Уравнение асимптот: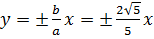

Сделать чертеж.

Тема 6. Пределы функций

Вычислить пределы.

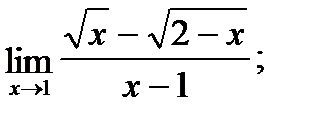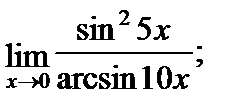7. а) б) в)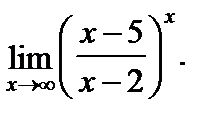

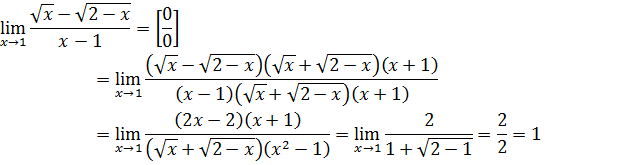
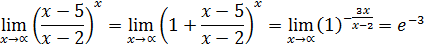
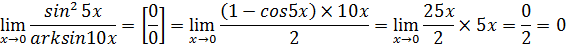
Тема 7. Основы дифференцирования

Найти производную сложной функции.

7. ; ;

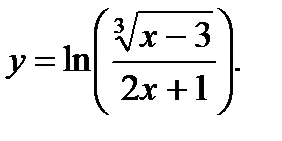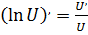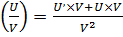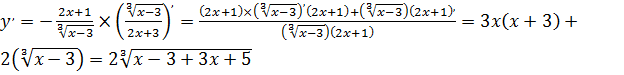Тема 8. Исследование функций

Исследовать функцию и построить ее график.

7.

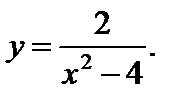1. Найдем область определения функции.

Функция 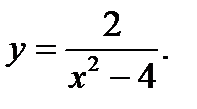определена на всем множестве вещественных чисел, кроме тех значений при которых знаменатель обращается в ноль: 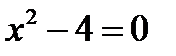при 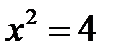, 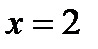; 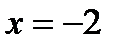, следовательно .

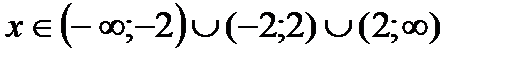2. Исследуем функцию на четность

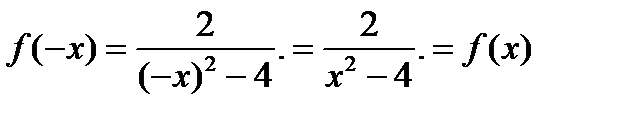
Данная функция является четной, т.е. ее график симметричен относительно оси ординат.

3. Найдем вертикальные асимптоты к графику функции.

Вертикальные асимптоты могут быть в точках разрыва графика функции x=2 и x=-2

При 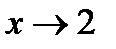слева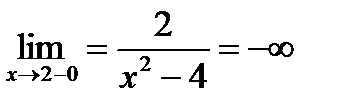

При 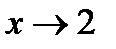справа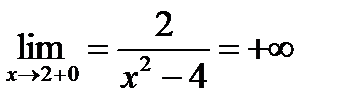

Таким образом, х=2 и х=-2(т.к. функция четная, симметричная) – вертикальные асимптоты.

4. Найдем горизонтальные и наклонные асимптоты:

Для этого найдем пределы функции пр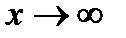и , и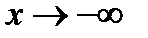

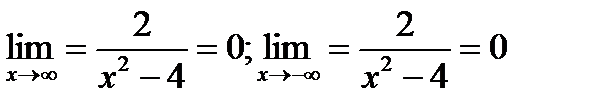, следовательно, прямая у=0 – горизонтальная асимптота

Для того чтобы найти наклонные асимптоты, нужно исследовать предел 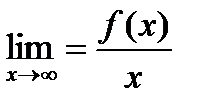. Если он существует и равен конечной величине 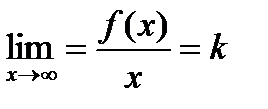, а также существует конечный предел 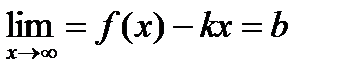, то прямая у=kx+b является наклонной асимптотой. В нашем случае 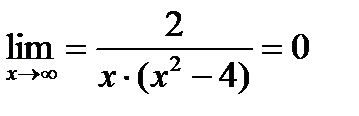, конечного предела не существует, наклонных асимптот нет.

5. Найдем экстремумы и интервалы монотонности функции

Для этого вычислим первую производную функции

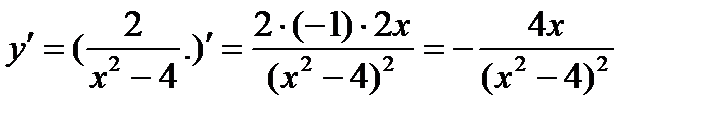
Найдем значения х при которых 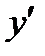обращается в ноль или не существует

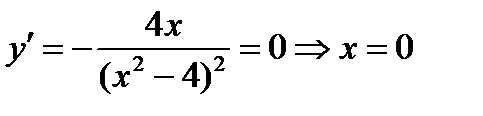
Производная не существует в точках х=2 и х=-2, но эти точки не входят в область определения функции, поэтому критической является только точка х=0.

+

-

На промежутке 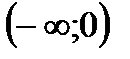первая производная 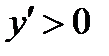функция возрастает

На промежутке 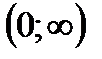первая производная 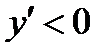функция убывает

Поскольку в точке х=0 производная меняет знак, точка х=0 является точкой максимума.

6.Найдем интервалы выпуклости и точки перегиба.

Для этого найдем вторую производную

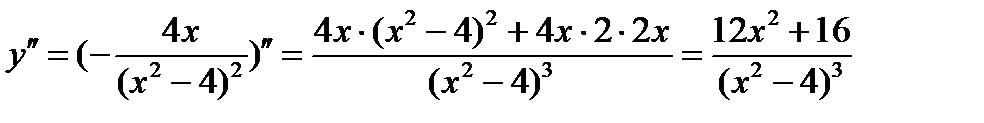
Точек, в которых вторая производная обращается в ноль нет, числитель будет всегда положительным, поэтому знак второй производной

определяется знаменателем m .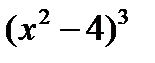

s c1BLAQItABQABgAIAAAAIQCFyneHXQQAAMIRAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9j LnhtbFBLAQItABQABgAIAAAAIQCVQU4D4AAAAAkBAAAPAAAAAAAAAAAAAAAAALcGAABkcnMvZG93 bnJldi54bWxQSwUGAAAAAAQABADzAAAAxAcAAAAA "> t ABQABgAIAAAAIQBvDPLdVwQAAMIRAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBL AQItABQABgAIAAAAIQBDk4Qf4AAAAAgBAAAPAAAAAAAAAAAAAAAAALEGAABkcnMvZG93bnJldi54 bWxQSwUGAAAAAAQABADzAAAAvgcAAAAA ">

+

+

-

-2

На промежутках 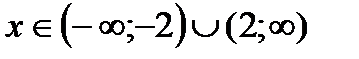вторая производная будет положительна, значит функция будет вогнута вниз.

На промежутке 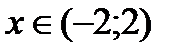вторая производная будет отрицательна, значит функция будет выпукла вверх.

7. Найдем точки пересечения графика функции с осями.

Полагаем, что x=0 тогда 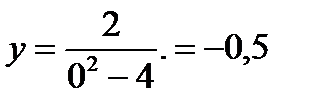, точка пересечения с осью ординат (0;-0,5)

y

Теперь предположим, что y=0. Нет таких значений x, которые бы удовлетворяли данному требованию. Поэтому график функции не пересекает ось абсцисс.

X=2

X=-2

Построим график.

x

-2

2

-0,5