Системы линейных уравнений

Системой линейных уравнений (СЛУ) называется система уравнений вида:

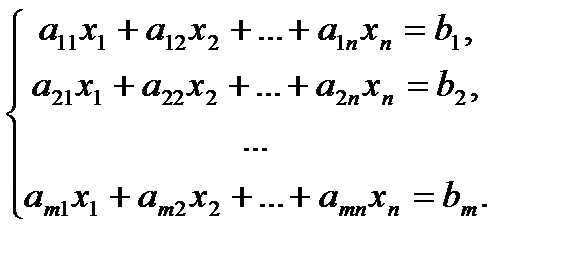
Система называется однородной, если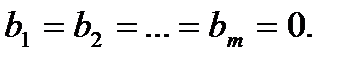

Матрица 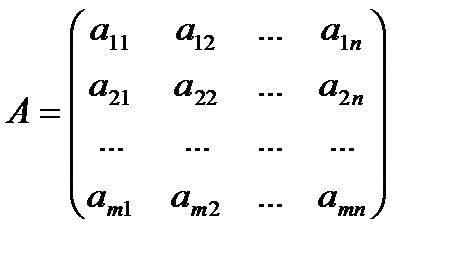называется матрицей коэффициентов.

Матрица 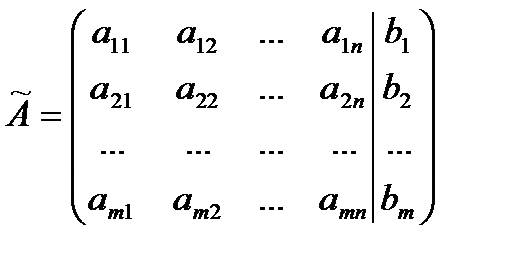называют расширенной матрицей системы.

Столбец 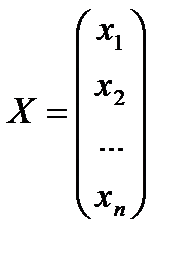называют столбцом неизвестных.

Столбец 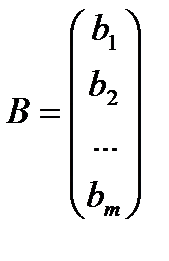называют столбцом свободных членов.

С учётом этих обозначений можно записать систему в матричной форме

.

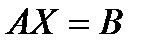Рассмотрим отдельно случай квадратной системы, когда 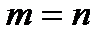, и общий случай, когда .

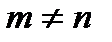1) Квадратная система

Пусть дана СЛУ, в которой 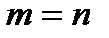и .

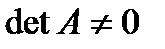Существуют три основных метода решения СЛУ:

а) метод Крамера

б) метод обратной матрицы

в) метод Гаусса

а) Обозначим

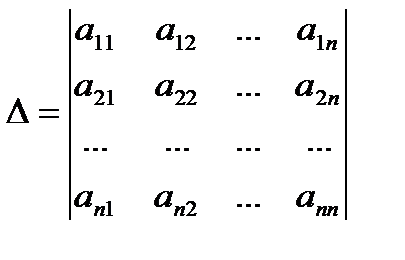
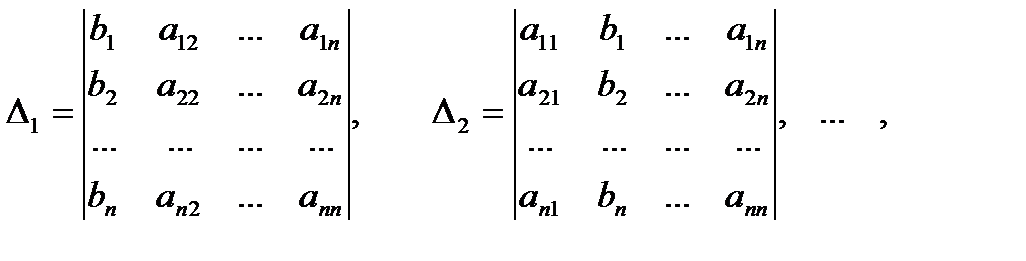
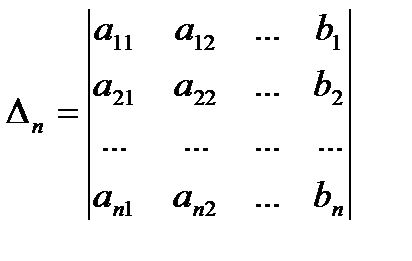
(определитель 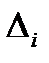получается из заменой i-го столбца на столбец свободных членов)

Тогда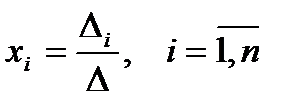

б) Рассмотрим СЛУ в матричной форме

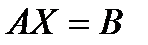
Домножим слева на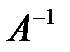

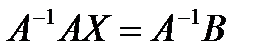
Но произведение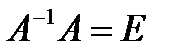

Таким образом

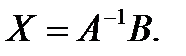
в) При решении СЛУ методом Гаусса, расширенную матрицу системы приводят к треугольному виду с помощью элементарных преобразований

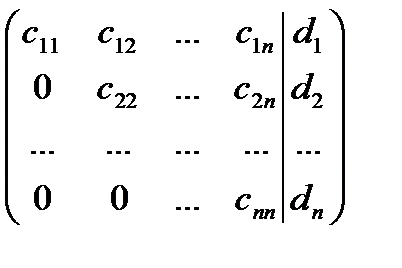
По данной матрице составляется система

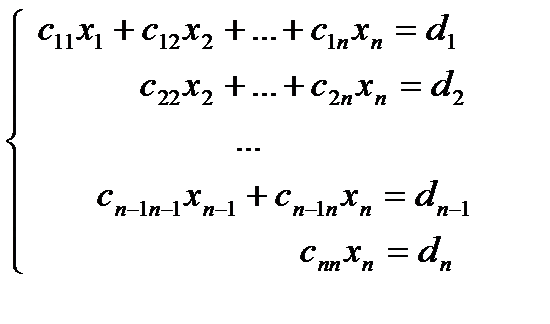
Из последнего равенства найдём 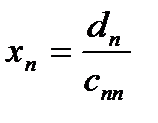и подставим его в предыдущее

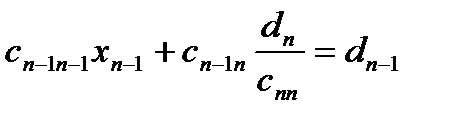
Из этого равенства найдём 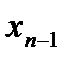и подставим в предыдущее и т.д.

2) Общий случай

Теорема Кронекера-Капелли

Система линейных уравнений совместна тогда и только тогда, когда

.

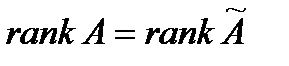В случае, когда число уравнений не равно числу неизвестных, систему удобно решать методом Гаусса, который состоит в приведении расширенной матрицы к трапецеидальному виду путём применения элементарных преобразований. Если при этом на некотором этапе получается строка, в которой все элементы, кроме столбца свободных членов, равны нулю, то система несовместна (это случай, когда 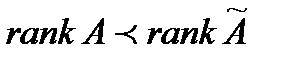). Если 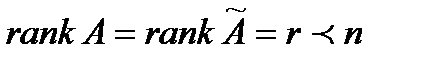, то система имеет бесконечно много решений, и каждое решение зависит от 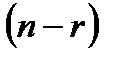не зависящих друг от друга параметров, т.е. степень свободы системы 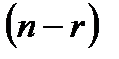. В качестве параметров удобно брать «лишние неизвестные», которые объявляются свободными, остальные переменные – базисные выражаются через свободные.

Однородная система линейных уравнений

Расширенная матрица отличается от матрицы коэффициентов наличием нулевого столбца, т.е. 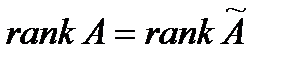. Значит, по теореме Кронекера-Капелли система всегда совместна. Одно решение очевидно - 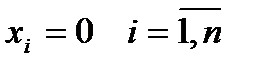. Это решение называется тривиальным. Если 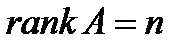, то решение единственное – тривиальное, если 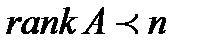, то решений бесконечно много.

Обозначим базисные неизвестные 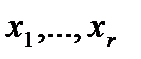, тогда

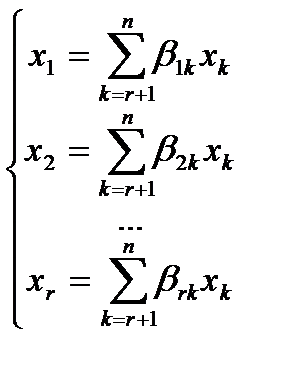
В матричной форме

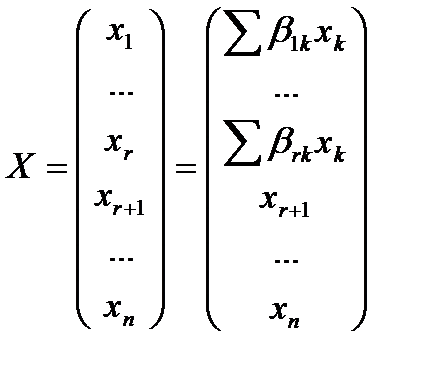
Можно записать так:

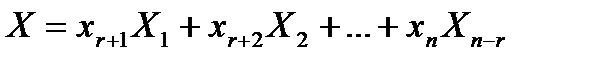, где

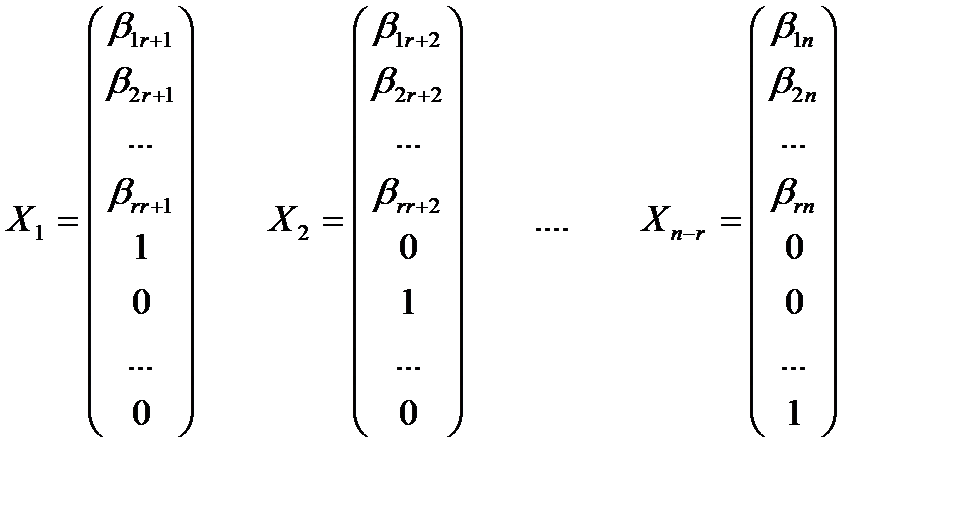
Решение 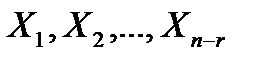называется фундаментальной системой решений (ФСР) однородной системы. Общее решение системы является линейной комбинацией фундаментальной системы решений.

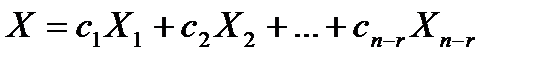
Примеры

1. Даны матрицы 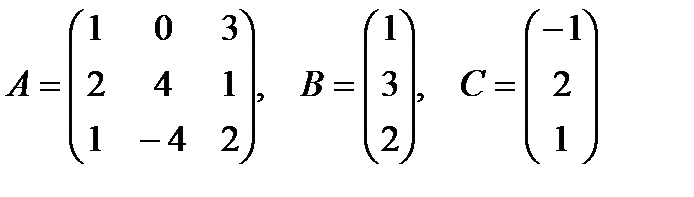и число 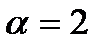. Найти .

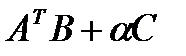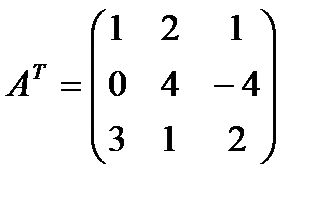
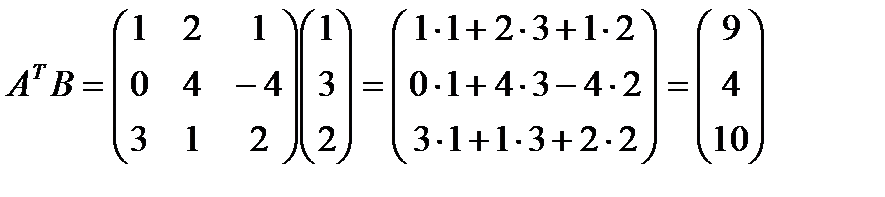
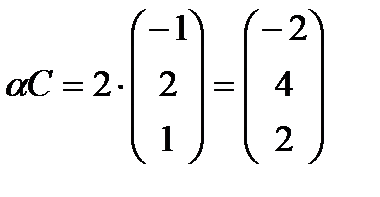
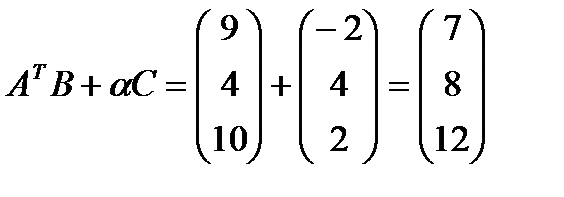
2. Дана матрица 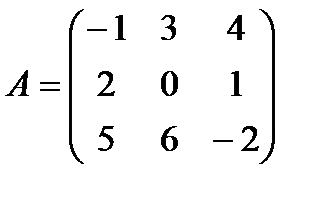. Найти .

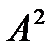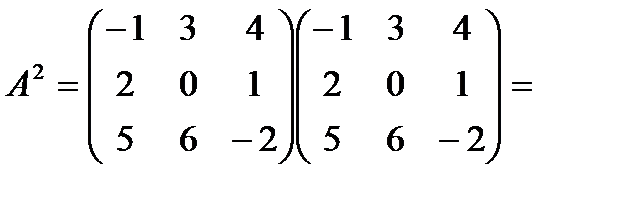
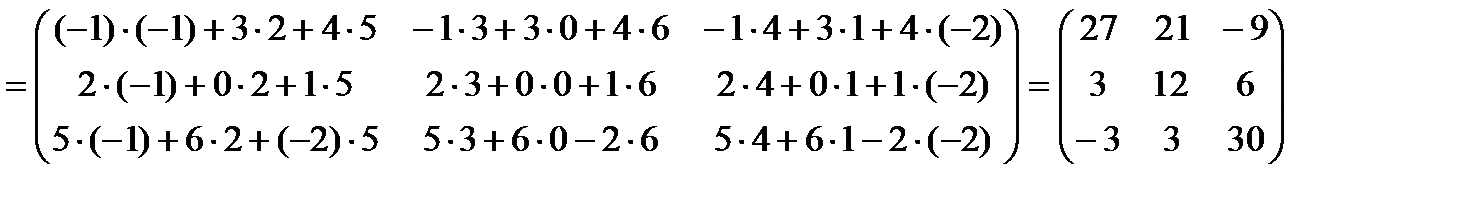
3. Даны матрицы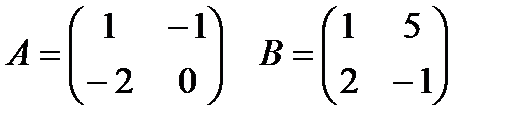

Найдите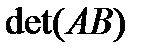

I способ.

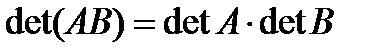
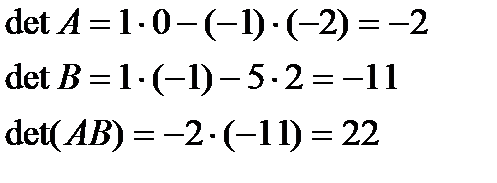
II способ.

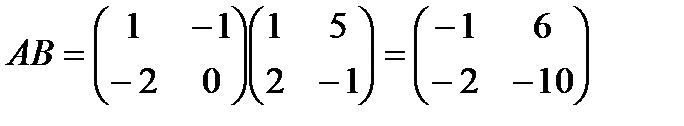
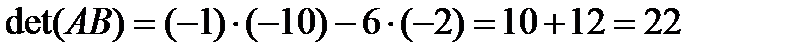
4. Вычислить определитель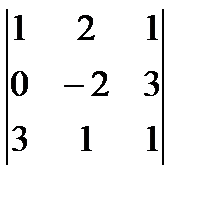

Вычислим определитель различными способами:

1) по правилу треугольников

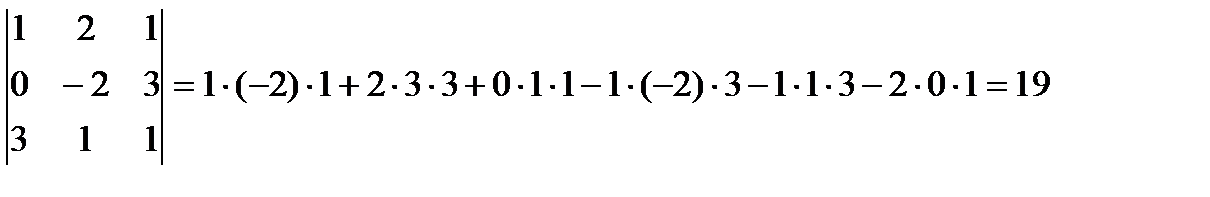
2) разложим определитель по первой строке

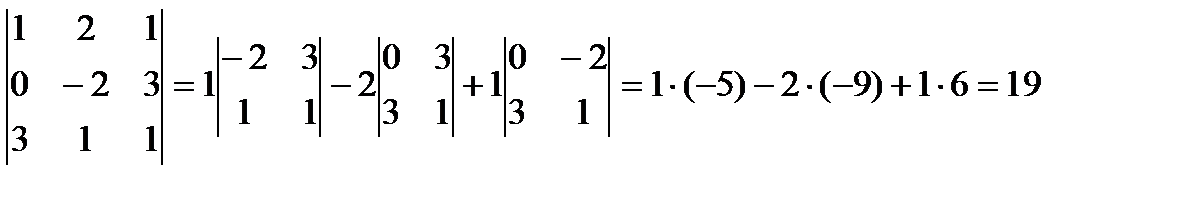
3) приведём определитель к треугольному виду

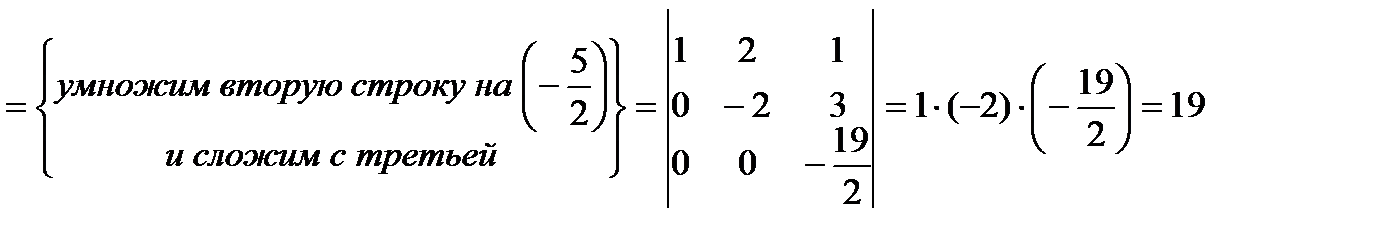
5. Вычислить определитель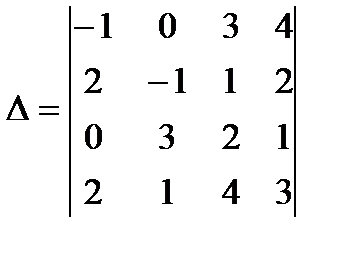

I способ.

Лучше разложить данный определитель по строке или столбцу, содержащим нули, т.к. наличие нуля уменьшает вычисления. Выберем, например, второй столбец.

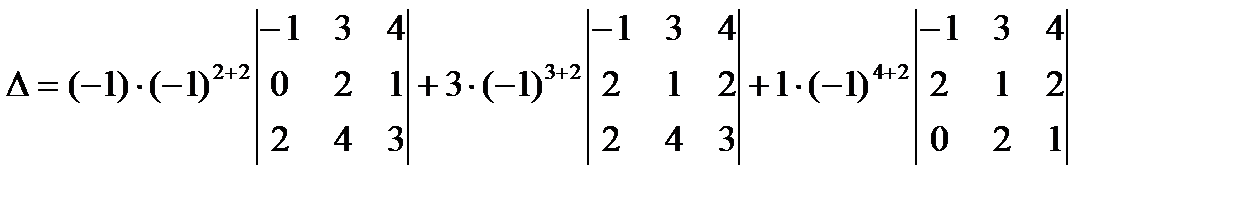
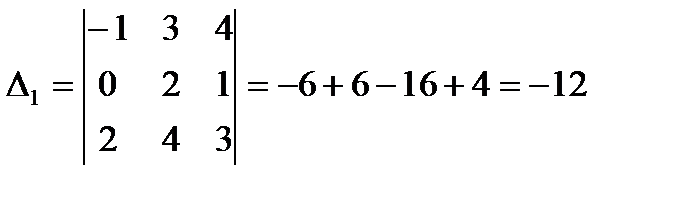
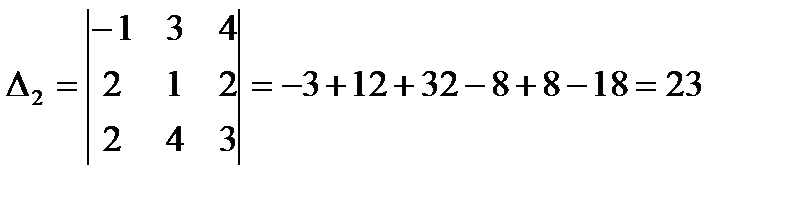
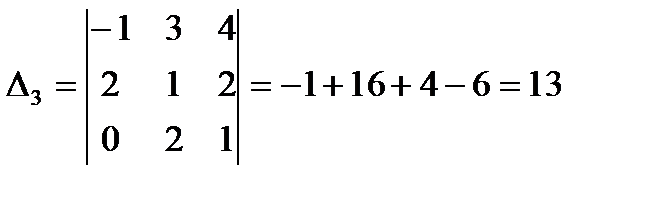
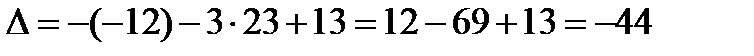
II способ.

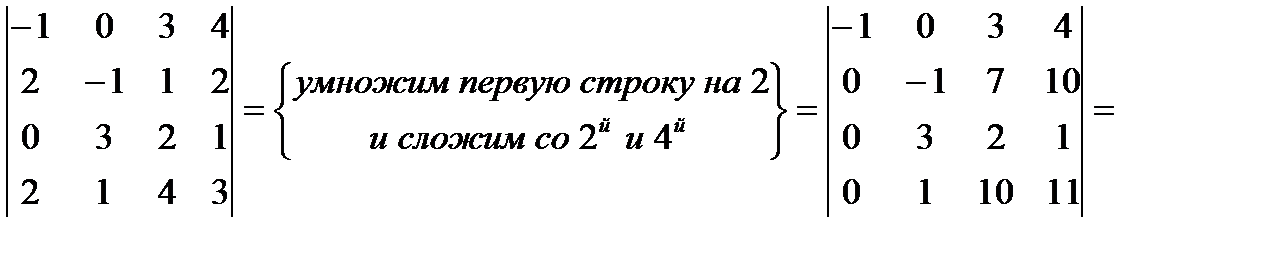
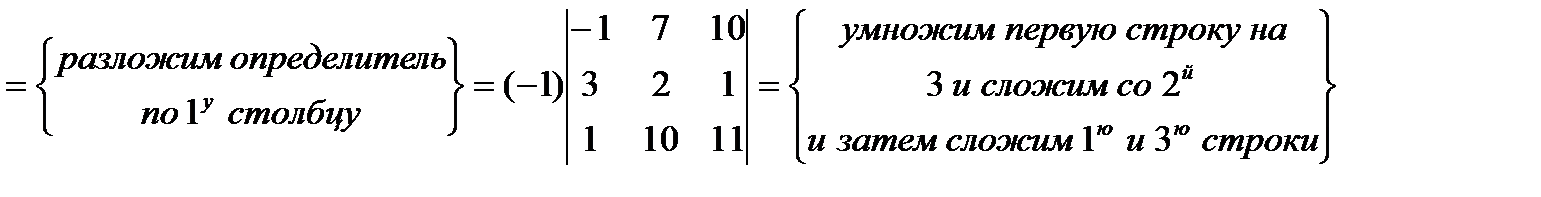
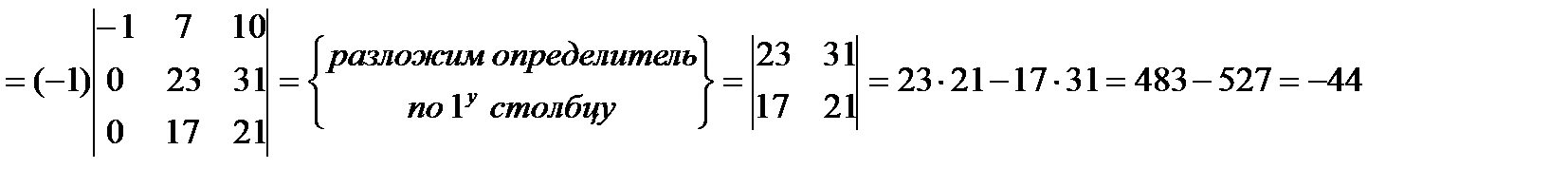
6. Найти 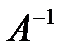, если 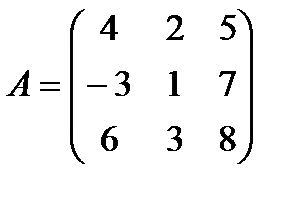. Сделать проверку.

1) 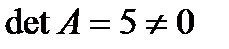, значит существует .

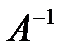2) Найдём алгебраические дополнения

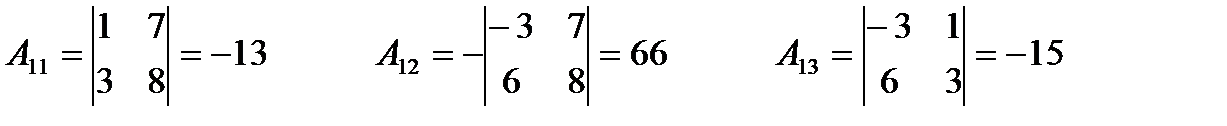
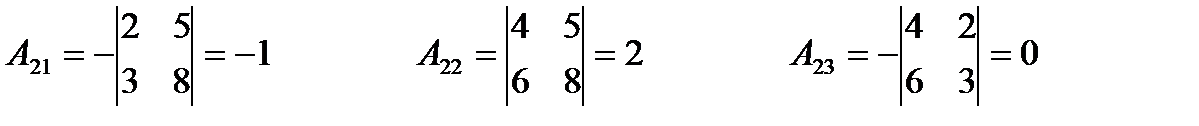
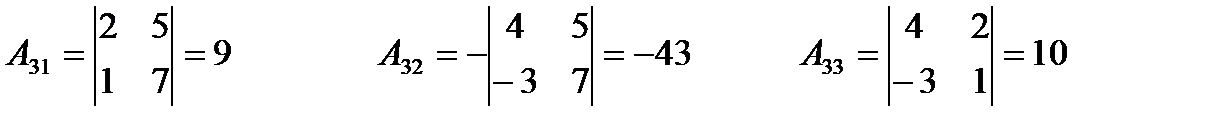
3)

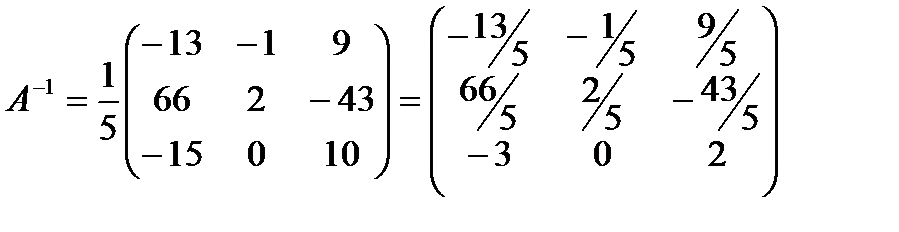
4) Проверка

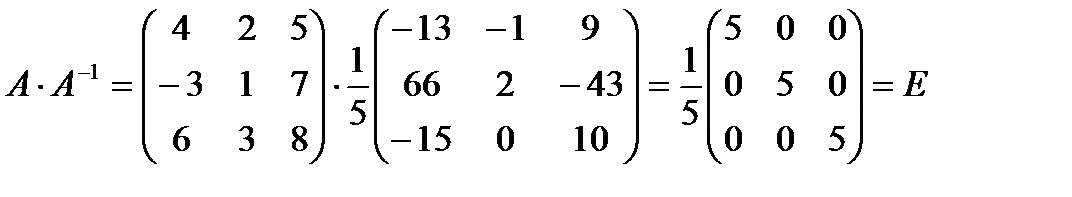
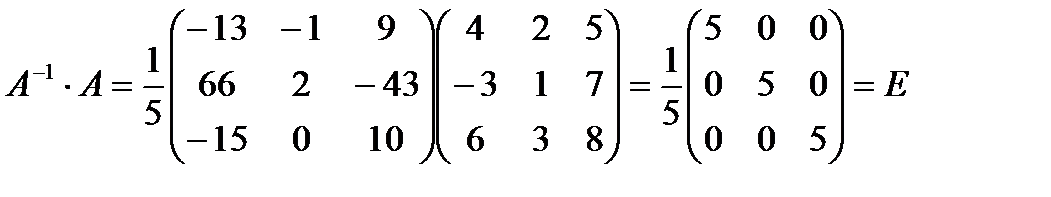
7. Методом элементарных преобразований найти 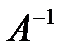для матрицы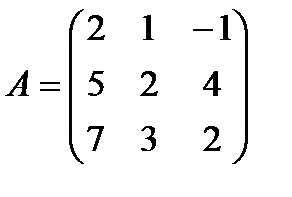

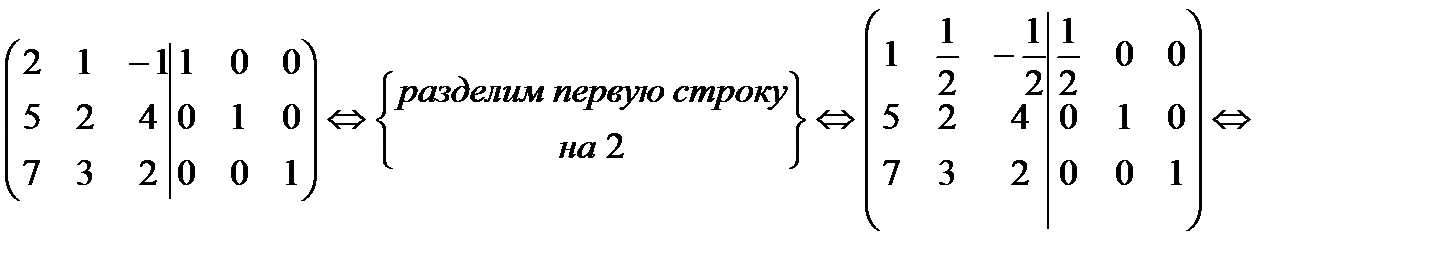
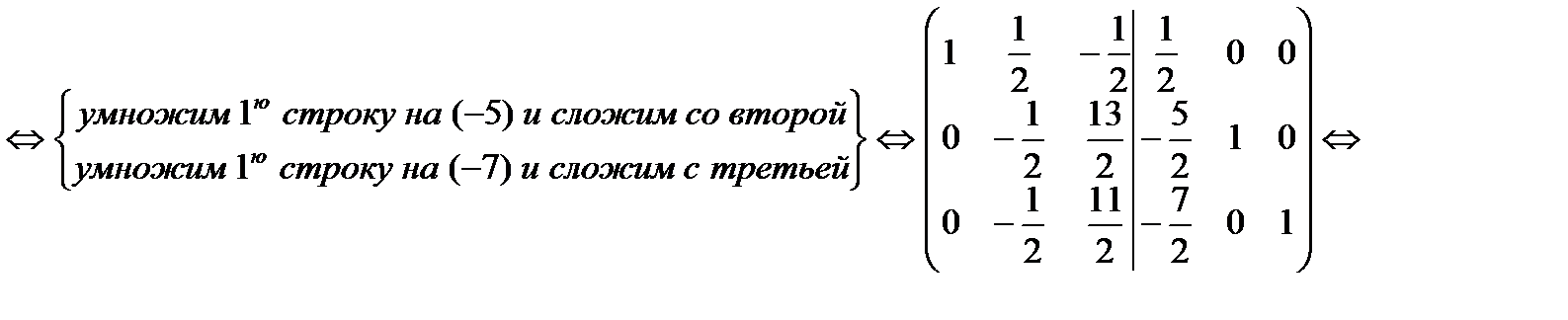
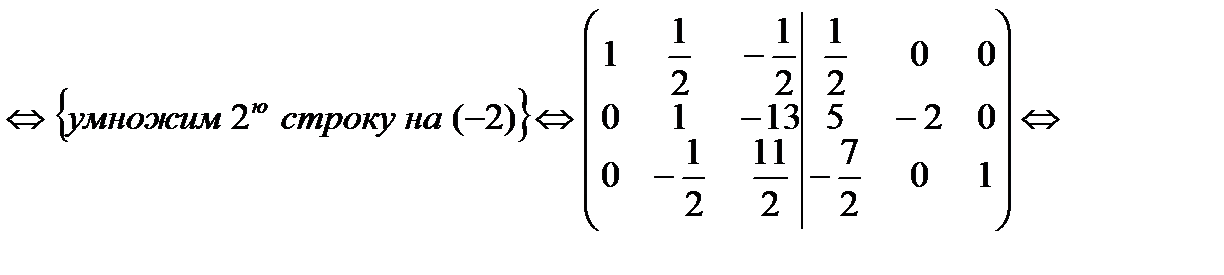
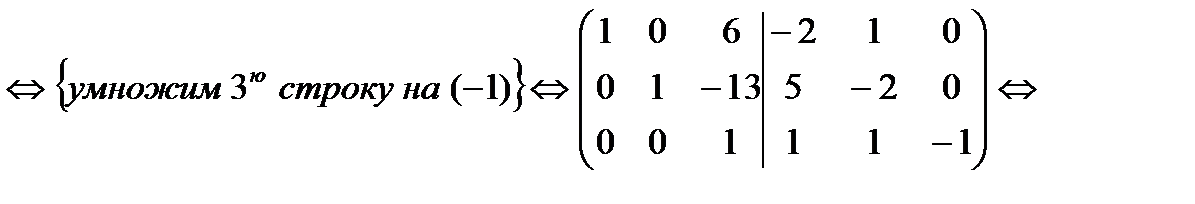
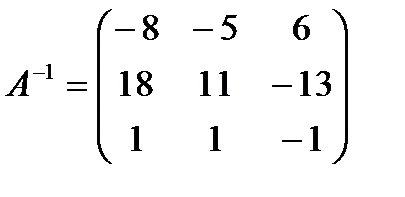
8. Найти ранг матрицы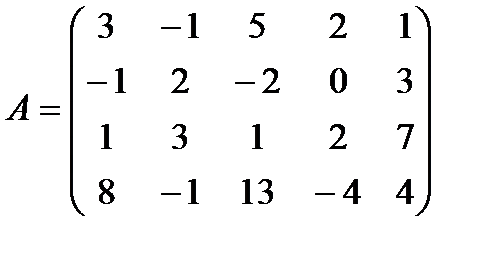

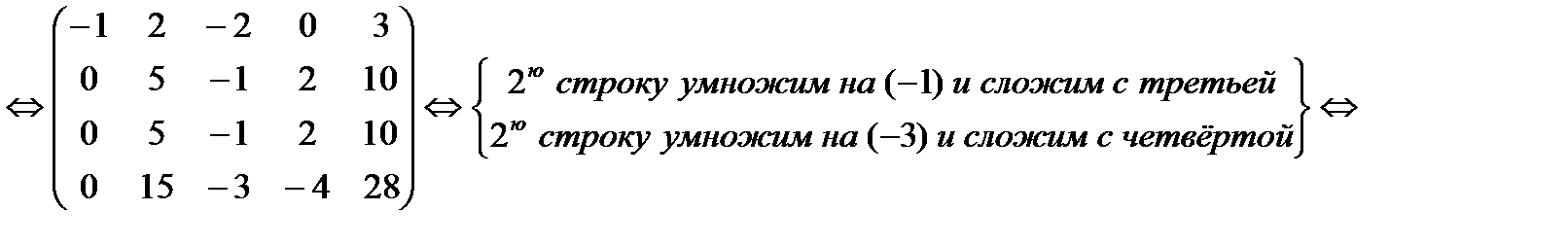
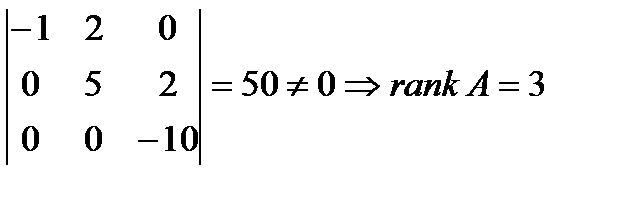
9. Решить систему уравнений

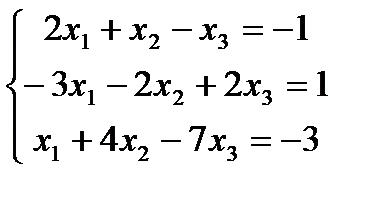
а) методом Крамера

б) матричным способом

в) методом Гаусса

а)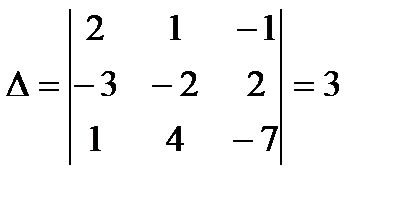

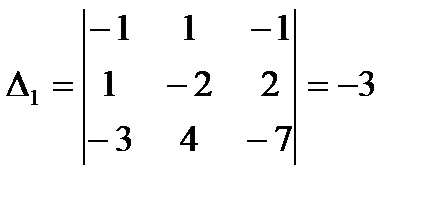
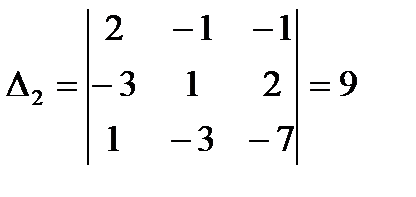
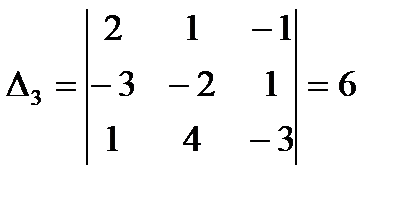
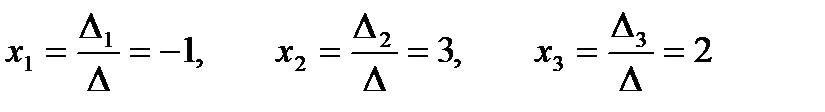
б)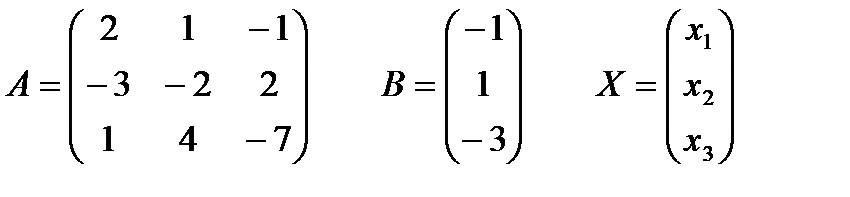

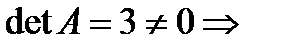существует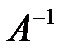

Найдём .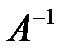

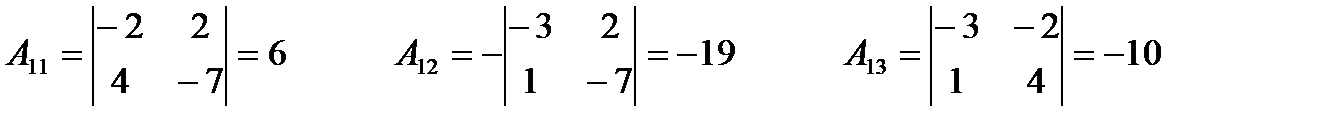
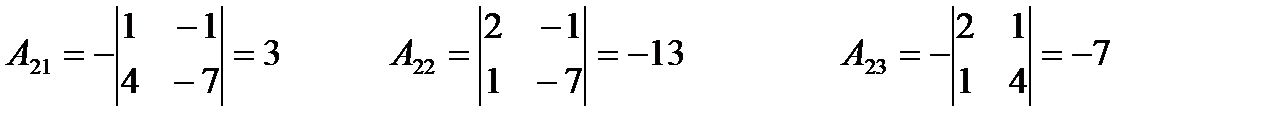
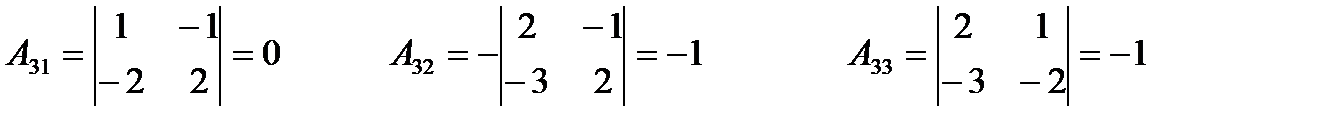
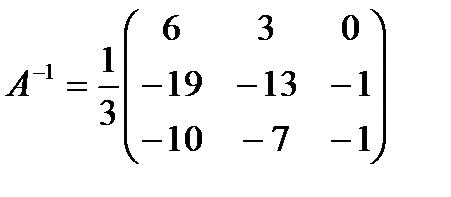
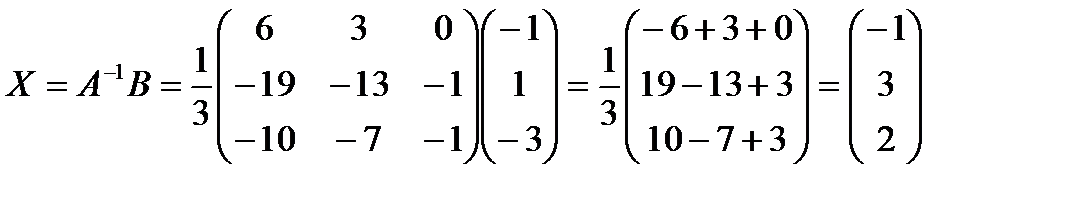
в)

По данной матрице запишем систему уравнений

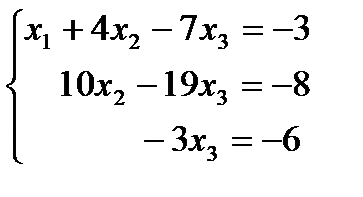
Из последнего уравнения найдём 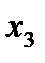, подставим его во второе уравнение, найдём 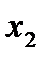, а затем из первого найдём .

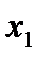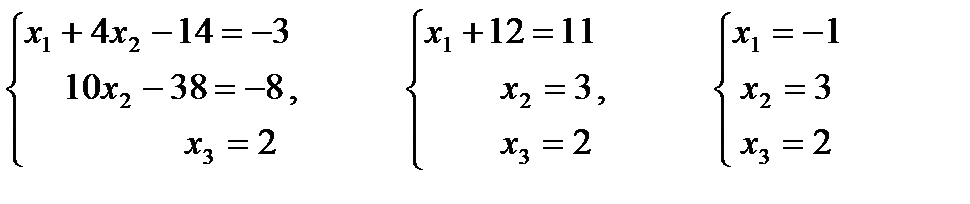
10. Определить совместность системы

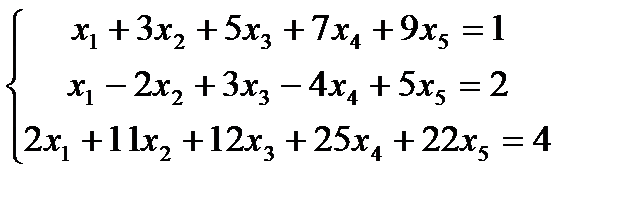
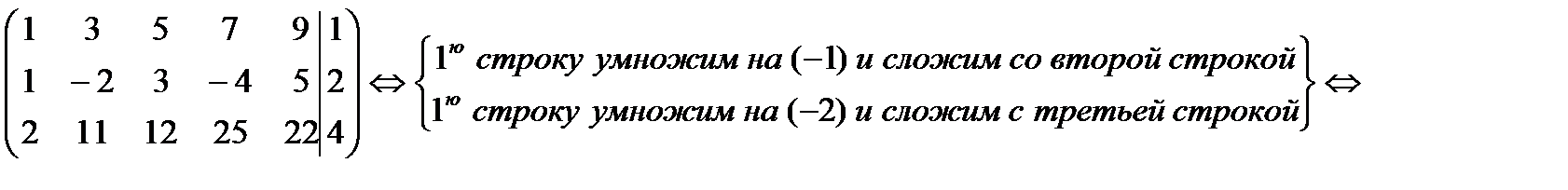
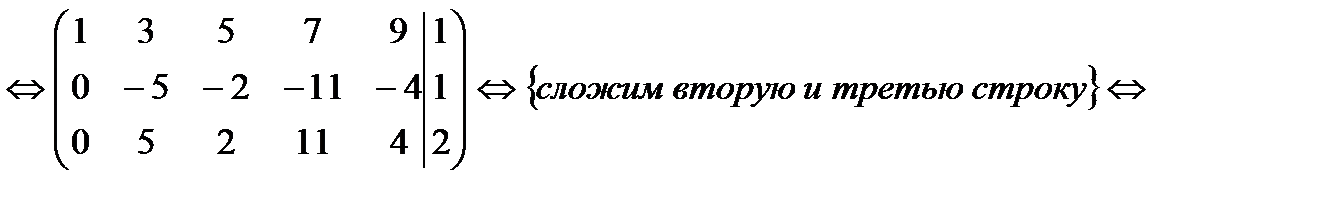
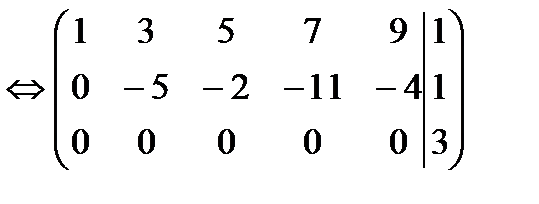
Ранг матрицы коэффициентов равен 2. Ранг расширенной матрицы равен 3. Следовательно, система несовместна.

11. Решить систему уравнений

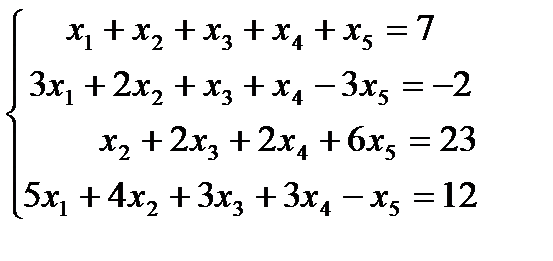
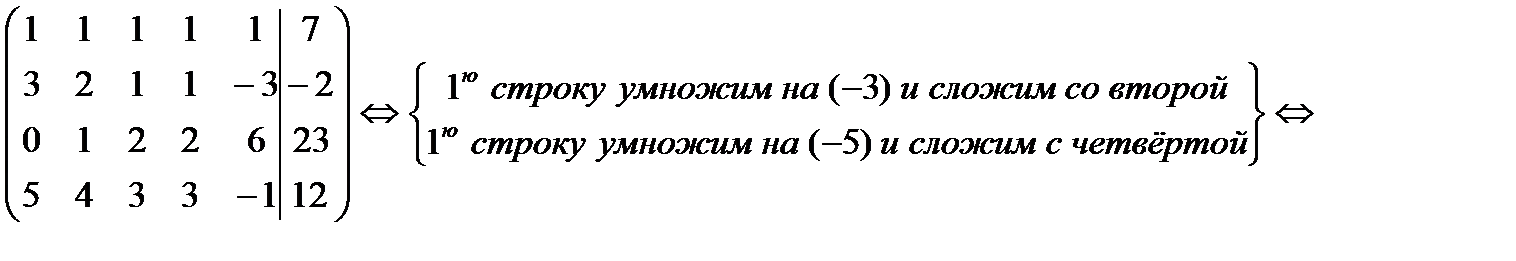
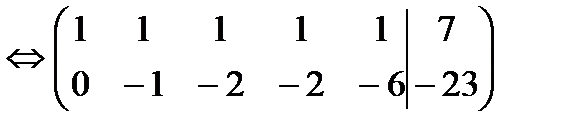
Матрица приведена к трапецеидальному виду, под главной диагональю элемент равен нулю. Полученная матрица является расширенной матрицей системы, равносильной исходной. Ранг этой матрицы совпадает с рангом исходной. Поэтому заключаем, что система совместна, т.к. ранг матрицы коэффициентов равен рангу расширенной матрицы и равен 2. Система будет иметь 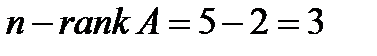свободных неизвестных и 2 базисных.

Пусть 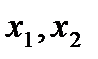- базисные переменные,

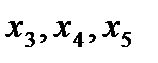- свободные

Тогда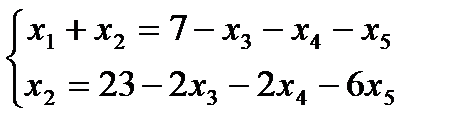

Выразим 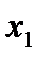из первого равенства через свободные

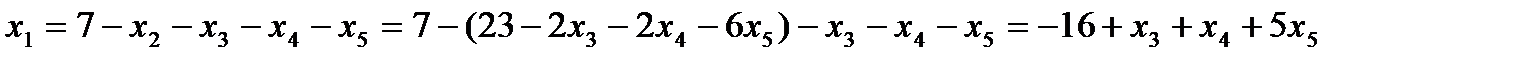
Общее решение может быть записано в виде

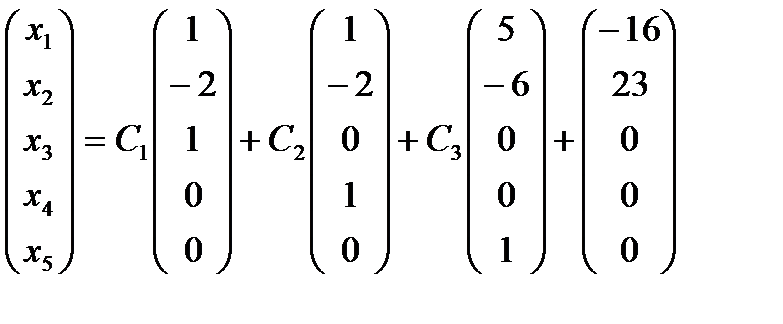
Замечание. Поскольку существует свобода выбора базисных и свободных переменных, то общее решение может быть записано в различных, но естественно, равносильных формах.

12. Решить систему уравнений.

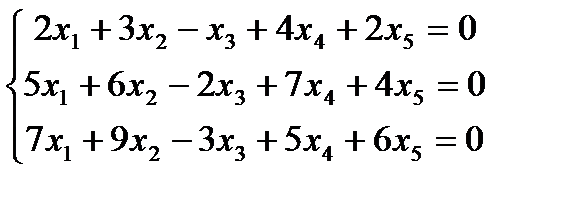
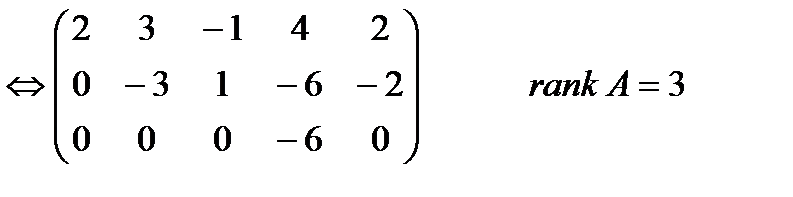
Запишем систему уравнений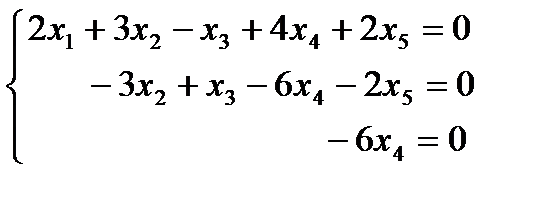

Из последнего уравнения 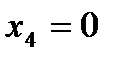. Так как 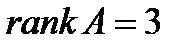, то в системе 3 базисные переменные и 2 свободные. Так как 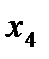однозначно определена, то она базисная и пусть 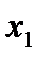и 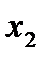- тоже базисные. Тогда 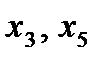- свободные. (За базисные неизвестные необходимо выбирать такие, при которых матрица коэффициентов не вырождена).

Выразим 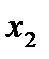из второго уравнения через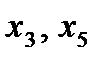

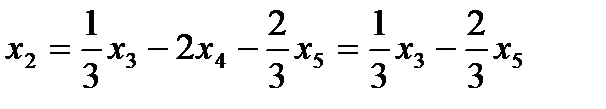
Из первого уравнения найдём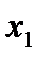

.

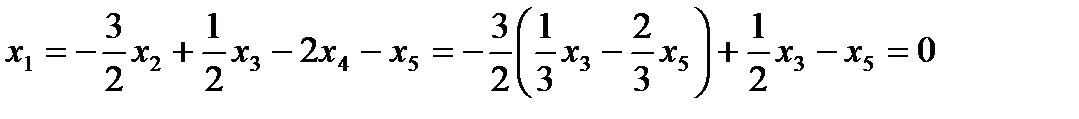Тогда общее решение системы имеет вид

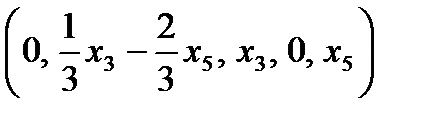, где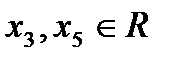

Обозначим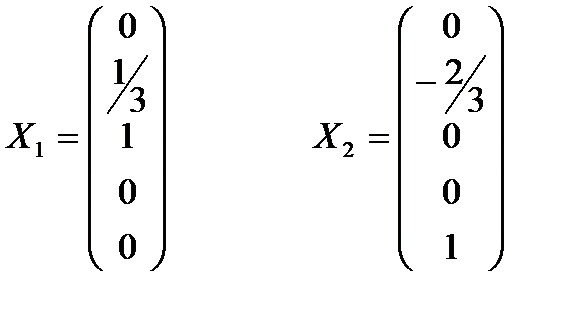

Эти векторы образуют фундаментальную систему решений.

Любое решение системы запишется в виде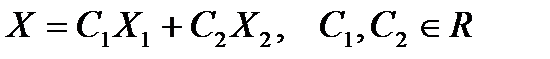

ТЕМА 2. ВЕКТОРНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ