Уравновешивание углов сети теодолитных ходов по способу полигонов профессора В.В.Попова

2.2.1. Задание.

Уравновесить углы и вычислить дирекционные углы сторон сети, изображенной на

рисунке 6.

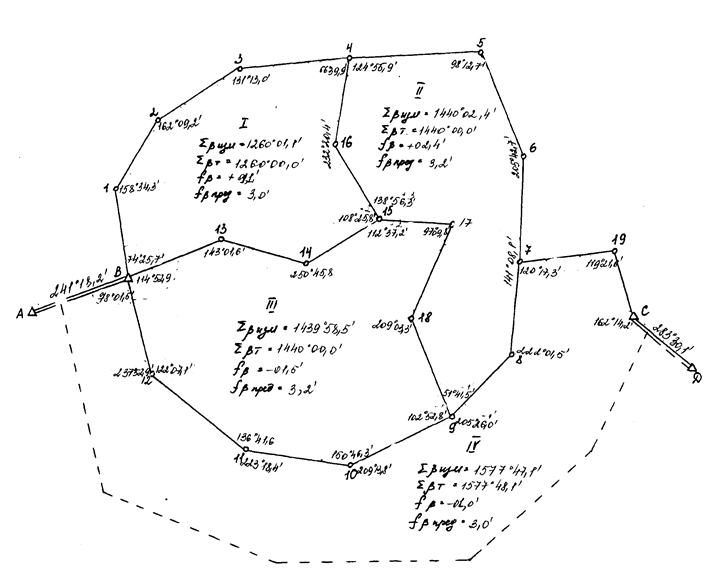
В таблице 15 по вариантам предложены начальный а вех и конечный Оср. дирекционные углы опорных линий АВ и СО .

Таблица 15

Исходные данные.

№№ вариантов	Дирекционные углы

2.2.2. Порядок решения.

2.2.2.1. Подсчитываем число полигонов, включая и несомкнутый полигон между твердыми (исходными) сторонамиАВ и CD.

2.2.2.2. Исправить непосредственно на схеме полигонов (рисунок б) сумму углов при каждой внутренней узловой точке (15 и 9) для соблюдения условий горизонта (360°), внеся поправки поровну. на каждый угол до десяти долей минуты. Поправки записываем на схеме у соответствующих углов в десятых долях минуты в скобках. Например, поправку +0,1' записываем в виде +1.

2.2.2.3. Подсчитываем сумму измеренных углов в каждом полигоне с учетом поправок за условие горизонта и записываем ее на схеме внутри соответствующего полигона (см. рисунок б). Несомкнутый полигон IV, включающий твердые линии АВ и CD условно считаем сомкнутыми при помощи пунктирной линии. Число углов, сторон или направлений по этой пунктирной линии в процессе вычислений считается равным нулю.

Под практической суммой углов в каждом полигоне записываем сумму углов теоретическую, причем по полигону IV теоретическую сумму углов следует вычислять по формуле:

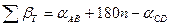(42)

Вычисляем для каждого полигона полученную невязку в сумме углов

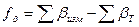(43)

и сравниваем ее с предельной 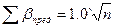(44)

где n- число углов полигона.

Полученные предельные невязки записываем на схеме (см. рис. б) под соответствующими суммами углов в каждом полигоне.

2.2.2.4. Составляем схему сети теодолитных ходов для уравновешивания углов (рисунок 7). На этойсхеме выписываем номера узловых точек и полигонов. Внутри каждого полигона под его номером заготовить табличку невязок и около каждого звена, кроме пунктирного, таблички поправок. В таблички записываем полученные невязки.

2.2.2.5. Вычисляем красные числа для каждого звена всех полигонов по правилу:

красное число звена равно числу направлений в звене деленному на число

направлений в звене, деленному на число направлений в полигоне.

При этом каждую линию в замкнутых полигонах |,||, и а в полигоне IV твердые

линии АВ и СD считаем каждую за одно направление. Поэтому на чертеже пунктирная линия, условно замыкающая полигон, вычерчивается у середины твердых линий, включая в полигоне не целые линии, а одно направление. Контроль: сумма красных чисел по каждого полигону должна быть точно равна единице. Красные числа выписать красным цветом под соответствующими табличками.

2.2.2.6. Распределяем невязки пропорционально красным числам соответствующих полигонов. Начинаем с полигона, имеющего наибольшую по абсолютной величине невязку, умножая, ее последовательно на красные числа звеньев данного полигона и вносим произведения в соответствующие таблички поправок со знаком невязки, с округлением до 0.1΄

2.2.2.7. Подсчитываем алгебраические суммы чисел, а таблицу поправок и записываем их над двойной чертой.

Подсчитываем поправки во внутренние углы каждого полигона по всем звеньям. Для внутренних звеньев сети поправки получаем так: изменяем, знак суммы чисел внешней по отношению к полигону таблички и складываем с суммой чисел внутренней таблички того же знака. Для каждого внешнего звена сети поправка равна итогу внешней таблички с противоположным знаком. Все поправки на звенья записываем в скобках внутри полигона у соответствующих звеньев (см. рис. 7).

Контроль вычислений поправок: их сумма по каждому полигону должна быть равна невязке полигона с обратным знаком.

Таблица 16

Ведомость вычисления дирекционных углов.

№№ точек	Углы	№ точек	Углы
Измер	Исправл.	Дирекц.	Измер.	Исправл.	Дирекц.
					б
А   В
C D

Уравновешивание системы полигонометрических ходов способом последовательных приближений

2.3.1. Задание.

По данным, указанным на схеме полигонометрических ходов (рис. 8, 9), способом последовательных приближений произвести уравновешивание:

• дирекционных углов узловой линий;

• координат узловых точек.

В таблице 17 приведены по вариантам углы при точках № 1,12,16. Остальные

углы принять такими же, как и на схеме (см. рис. 8).

Таблица 17 Значения углов № 1,12,16.

№№ варианта	Углы

В таблице 18 приведены суммы приращений координат в звеньях по вариантам.

Таблица 18 Суммы приращений координат по звеньям.

№№ варианта	Суммы приращений координат
Звено 1	Звено 2	Звено 3	Звено 4	Звено 5	Звено б

2.3.2.2 Порядок уравновешения.

2.3.2.1.Вычисление дирекционных углов.

2.3.2.1.1. На схематическом чертеже (см. рис. 8) у каждого звена выписываем в виде дроби: в числителе номер звена и сумму измеренных углов, в знаменателе - число углов (звеном называют часть хода, заключенногомежду угловыми линиями или между «твердой» и узловой линией)

2.3.2.1.2. По данным, представленным на чертеже, подсчитываем угловые невязки по ходам и замкнутому полигону и выписываемих на чертеж (см. рис. 8). Если угловые невязки не превышают допустимой, то продолжаем вычисление.

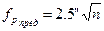
2.3.2.1.2. Заполняем ведомость вычисления дирекционных углов (таблица 19) в следующем порядке:

• выписываем исходные данные дирекционные углы «твердых» линий с чертежа сети;

• в графу 1 выписываем название узловых линий, для которых вычисляются дирекционные углы;

• в графу 2 выписываем наименование начальных (исходных) линий (твердых и узловых) звена, от которых можно вычислить искомые дирекционные углы, при этом в первую очередь выписываем наименование «твердых», исходных сторон;

• в графу 3 выписываем номера звеньев примыкающих к соответствующей узловой (искомой) линии, графы 4, 5 и 6 заполняем со схемы ходов в соответствии с их названием;

• вычисляем веса дирекционных углов по каждому звену (до 0,01) по формуле:

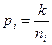(46)

где i = 1,2,3,... „- номер звена;

k - произвольный постоянный коэффициент обычно выбираем так, чтобы веса выражались числами близкими к единице;

n_i - число углов звена.

Для дирекционного угла каждой узловой линии вычисляем сумму весов

примыкающих к ней звеньев и определяем веса по формуле:

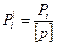(47)

Контроль:[P΄]=1

• вычисляем методом последовательных приближений значения дирекционных

углов узловых линий.

Нулевое приближение для дирекционных углов каждой узловой линии вычисляем непосредственно от « твердой» стороны:

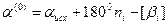(48)

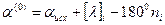(49)

Нулевое приближение записываем в первых строках каждого блока графы 9 и подчеркиваем;

• для вычисления первого приближения дирекционного угла каждой узловой линии находим значения дирекционного угла этой линии путем передачи от исходных данных по воем примыкающим к ней звеньям. Из полученных значений найти среднее весовое значение (графы 9,10)

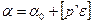(50)

гдеα₀ - приближенное (наименьшее) значение дирекционного угла узловой линии (взятое до целых минут) из полученных значений по каждому примыкающему звену:

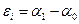(51)

Это и будет первым приближением.

Аналогично вычисляем второе, а затем и следующие приближения (графы 11,...). При вычислении каждого последующего приближения за исходные данные принимаем самые последние значения приближений.

Приближения заканчиваем,

тогда когда последнее вычисленное приближение дает одинаковый результат с предыдущим. Это последнее приближение и является окончательным значением о. Величины ε_i и α вычисляем до целых секунд;

• для контроля вычислений определяем поправки в углы по звеньям.

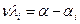(углы левые), (52)

где α и α_i - значения дирекционных углов соответственно узловой линии, записанные в графы последнего приближения, и окончательное. Выполнение равенства:

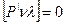(53)

служит контролем правильности вычисления окончательного значения

дирекционного угла.

Из-за погрешностей округления Σ P`_iν_i может быть не равно нулю, но должна быть

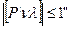(54)

Значения поправок ν_i выписать на схему ходов (см. рис. 8) красным цветом над суммой измеренных углов соответствующего звена и произвести подсчет поправок по ходам, имея в виду, что

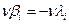(55)

т.е. в случае правых углов знак полученной поправки должен быть изменен на

противоположный.

Контроль: сумма поправок по ходу должна быть равна невязке с обратным знаком.

Таблица 19