Зона рассеяния центра электрических нагрузок промышленного предприятия
До сих пор все рассуждения по определению ЦЭН, наивыгоднейшего места расположения источника питания, изучению распределения нагрузок на территории проектируемого объекта велись при условии, что нагрузки приёмников являются фиксированными величинами. Поэтому ЦЭН определялся как некоторая стабильная точка. Однако каждый приёмник электроэнергии, цех и промышленное предприятие работают в соответствии с графиком нагрузок, причём нагрузки приёмников с течением времени (например, смены, суток) изменяются в соответствии с технологическим процессом производства. Поэтому при таких условиях не имеет смысла говорить о ЦЭН как о стабильной точке, координаты ЦЭН в каждый момент времени будут принимать значения, определенные нагрузками графика.
Рассмотрим приёмники электроэнергии промышленного предприятия.
Пусть для каждого приёмника электроэнергии заданы графики нагрузок  , где
, где 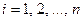 ;
;  , тогда координаты ЦЭН промышленного объекта являются значениями функции времени
, тогда координаты ЦЭН промышленного объекта являются значениями функции времени
 . (51)
. (51)
Для сокращения записей введём обозначения
 .
.
Величина  представляет собой отношение нагрузки приёмника с номером
представляет собой отношение нагрузки приёмника с номером  к суммарной нагрузке всех приёмников объекта в один и тот же момент времени
к суммарной нагрузке всех приёмников объекта в один и тот же момент времени  . Эту величину будем называть относительной нагрузкой приёмника с номером
. Эту величину будем называть относительной нагрузкой приёмника с номером  в момент времени
в момент времени  . На основании этого обозначения значения функции координат ЦЭН равны
. На основании этого обозначения значения функции координат ЦЭН равны
 . (52)
. (52)
Эти функции описывают перемещение ЦЭН; значения их, вычисленные в дискретные моменты времени  , образуют множество точек G, заполняющих некоторую область (рис. 6), которую называют зоной рассеяния ЦЭН. Размеры, форма зоны рассеяния, её центр определяют область наивыгоднейшего расположения источника питания на территории промышленного предприятия. Положения ЦЭН в зоне рассеяния зависят от координат мест расположения приёмников в группе и от их относительных нагрузок в данный момент времени.
, образуют множество точек G, заполняющих некоторую область (рис. 6), которую называют зоной рассеяния ЦЭН. Размеры, форма зоны рассеяния, её центр определяют область наивыгоднейшего расположения источника питания на территории промышленного предприятия. Положения ЦЭН в зоне рассеяния зависят от координат мест расположения приёмников в группе и от их относительных нагрузок в данный момент времени.
Следовательно, зона рассеяния ЦЭН является геометрической характеристикой взаимного расположения приёмников объекта и измерений их нагрузок во времени, а функция (52) её аналитическим выражением.
Центр зоны рассеяния определим соотношениями
 . (53)
. (53)
где  – осреднённое по времени значение относительной нагрузки
– осреднённое по времени значение относительной нагрузки  -го приёмника. Простейшими характеристиками зоны рассеяния являются отклонения координат ЦЭН от центра зоны в каждый момент времени t
-го приёмника. Простейшими характеристиками зоны рассеяния являются отклонения координат ЦЭН от центра зоны в каждый момент времени t
 . (54)
. (54)

Рис. 6. Множество точек ЦЭН
Внесём в (54) выражения для  ,
,  и
и  ,
,  из (52) и (53), найдём, что
из (52) и (53), найдём, что
 , (55)
, (55)
где  – отклонения относительных нагрузок приёмников с номерами
– отклонения относительных нагрузок приёмников с номерами 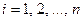 от средних значений.
от средних значений.
Величины  и
и  могут быть как положительными, так и отрицательными, они не зависят от параллельного сдвига системы координат, так как
могут быть как положительными, так и отрицательными, они не зависят от параллельного сдвига системы координат, так как
 (56)
(56)
Дальнейшее изучение зоны рассеяния связано с рассмотрением центральных моментов 2-го порядка отклонений
 (57)
(57)
Моменты  и
и  измеряют осреднённые по времени квадраты отклонений ЦЭН от центра зоны вдоль осей
измеряют осреднённые по времени квадраты отклонений ЦЭН от центра зоны вдоль осей  и
и  ; они являются показателями разброса координат ЦЭН нагрузок вдоль осей. Смысл величины
; они являются показателями разброса координат ЦЭН нагрузок вдоль осей. Смысл величины  раскрывается аналогично тому, как был раскрыт в разделе «Задача о числе источников питания» смысл компоненты
раскрывается аналогично тому, как был раскрыт в разделе «Задача о числе источников питания» смысл компоненты  тензора (30). Величина
тензора (30). Величина  является моментом связи отклонений
является моментом связи отклонений  и
и  . Внесём в правые части равенств (57) вместо отклонений их выражения из (55), получим
. Внесём в правые части равенств (57) вместо отклонений их выражения из (55), получим
 (58)
(58)
В этих формулах символом  обозначены ковариации относительных нагрузок приёмников с номерами i и j
обозначены ковариации относительных нагрузок приёмников с номерами i и j
 . (59)
. (59)
При  ковариация
ковариация  является дисперсией относительной нагрузки i-го приёмника. Далее заметим, что центральные моменты (58) обладают следующими свойствами:
является дисперсией относительной нагрузки i-го приёмника. Далее заметим, что центральные моменты (58) обладают следующими свойствами:
а) при параллельном сдвиге исходной системы координат  вдоль осей
вдоль осей  и
и  на величины а и b соответственно координаты ЦЭН группы приёмников преобразуют по формулам (5), а величины
на величины а и b соответственно координаты ЦЭН группы приёмников преобразуют по формулам (5), а величины  ,
,  и
и  остаются неизменными:
остаются неизменными:
 ; (60)
; (60)
б) при повороте исходной системы координат на угол  координаты ЦЭН группы приёмников преобразуют по (7), а эти же величины по формулам
координаты ЦЭН группы приёмников преобразуют по (7), а эти же величины по формулам
 (61)
(61)
Оба свойства устанавливают подстановкой соответствующих формул (5) или (7) в (58). Из второго свойства следует, что моменты (58) являются компонентами симметрического тензора 2-го порядка. Они выражаются в любой системе координат через исходные по (61), которые положены в определение этого тензора. По этим формулам вычисляют показатели разброса отклонений вдоль осей  и
и  и момент связи этих отклонений в любой системе координат. Тензор (58) будем называть тензором отклонений ЦЭН группы приёмников.
и момент связи этих отклонений в любой системе координат. Тензор (58) будем называть тензором отклонений ЦЭН группы приёмников.
В разделе «Тензорная природа характеристических свойств распределения нагрузок приёмников» показано, что тензор геометрически иллюстрируется эллипсом. Уравнение эллипса тензора отклонений ЦЭН группы приёмников имеет вид:
 , (62)
, (62)
которое получаем подстановкой (33) во второе равенство (58). Надо иметь в виду, что в (33) координаты х и у текущей точки линии заменены соответственно на  и
и  .
.
Зона рассеяния ЦЭН приёмников электроэнергии имеет форму, подобную эллипсу тензора. Таким образом, зона рассеяния ЦЭН цеха или промышленного предприятия при соответствующем подборе величины  ограничена эллипсом тензора.
ограничена эллипсом тензора.
[1] Разложение показателя разброса нагрузок на составляющие
[2] упорядоченное в виде строки, матрицы, параллелепипеда множество математических элементов.
