Пример решения транспортной задачи
Задача. Поставщик товара – оптовые коммерческие предприятия А1, А2, А3, А4 имеют запасы товаров а1=280, а2=350, а3=415, а4=255 единиц и розничные торговые предприятия В1, В2, В3 – подали заявки на закупку товара в объемах b1=620, b2=490, b3=150 единиц.
 Тарифы перевозок единицы груза с каждого из пунктов поставки в соответствующие пункты потребления заданы матрицей перевозок:
Тарифы перевозок единицы груза с каждого из пунктов поставки в соответствующие пункты потребления заданы матрицей перевозок:
4 17 7
C= 14 20 8
18 5 4
3 2 11
Найти такой план перевозки груза от поставщиков к потребителю, чтобы совокупные затраты на перевозку были минимальными.
Решение.
1) Проверим необходимое и достаточное условие разрешимости задачи:
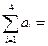 280 + 350 + 415 + 255 = 1300
280 + 350 + 415 + 255 = 1300
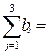 630+490+150 = 1260
630+490+150 = 1260
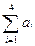 >
> 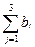 , следовательно, модель исходной
, следовательно, модель исходной
транспортной задачи является открытой.
Чтобы получить закрытую модель, введем фиктивного потребителя В4 с заявкой на Ь4=40 единиц товара. Тарифы перевозки для В4 полагаем равными нулю. Занесем данные в таблицу 16.
Табл. 16
 bj ai bj ai | ||||
2) Используя метод «северо-западного угла» построим первый опорный план.
Табл. 17
 bj ai bj ai | ||||
| 2804 | -17 | -7 | -0 | |
| 34014 | 1020 | -8 | -0 | |
| -18 | 4155 | -4 | -0 | |
| 2553 | 652 | 15011 | 400 |
Число занятых клеток - 7, а должно быть т+п-1=4+4-1=7. Следовательно, опорный план является невырожденным. Значение целевой функции плана 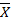 1:
1:
F (  )= 280∙4+340∙14+10∙20 + 415∙5+65∙2+150∙ 11 + 40∙ 0 = 9935
)= 280∙4+340∙14+10∙20 + 415∙5+65∙2+150∙ 11 + 40∙ 0 = 9935
3) Проверим оптимальность плана 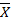 1 для этого дополним таблицу 17 столбцом и строкой потенциалами.
1 для этого дополним таблицу 17 столбцом и строкой потенциалами.
Табл. 18
 bj ai bj ai | ui | ||||
| 2804 | -17 | -7 | -0 | u1=0 | |
| 34014 | 1020 | -8 | -0 | u2=10 | |
| -18 | 4155 | -4 | -0 | u3= - 5 | |
| 2553 | 652 | 15011 | 400 | u4= - 8 | |
| vj | v1=0 | v2=10 | v3=19 | 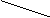  v4=8 v4=8 |
Найдем потенциалы по занятым клеткам uj + ui = cij и занесем в таблицу 18.
u1+v1=4 ] u1=0
u2+v1=14 v1=4
u2+v2=20 u2=10
u3+v2=5 v2=10
u4+v2=2 u3=-5
u4+v3=11 u4=-8
u4+v4=0 v3=19
v4=8
Оценим пустые клетки  ij=cij – ( ui + vj).
ij=cij – ( ui + vj).
 12=17 – (0+10) = 7
12=17 – (0+10) = 7
 13=7 – (0+19) = - 12
13=7 – (0+19) = - 12
 14=0 – (0+8) = - 8
14=0 – (0+8) = - 8
 23= 8 – (10+9) = - 21
23= 8 – (10+9) = - 21
 24=0 - (10+8 )= - 18
24=0 - (10+8 )= - 18
 31=18– (-5 – 4) =19
31=18– (-5 – 4) =19
 33=4 – (-5 +19) = -10
33=4 – (-5 +19) = -10
 34=0- (-5+8) = -3
34=0- (-5+8) = -3
 44=3 – (-8 +4) =7
44=3 – (-8 +4) =7
Первый опорный план не является оптимальным, т.к. среди этих оценок есть отрицательные, поэтому переходим к улучшению плана  1 .
1 .
4) «Худшую» оценку  23= - 21 имеет клетка (2,3). Построим для нее цикл перераспределения груза.
23= - 21 имеет клетка (2,3). Построим для нее цикл перераспределения груза.

 10 0 0 10
10 0 0 10




 +
+

 65 150 75 140
65 150 75 140
+ 
В результате получим новый опорный план 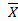 2 :
2 :
Табл. 19
 bj ai bj ai | ui | ||||
| 2804 | -17 | -7 | -0 | u1=0 | |
| 34014 | -20 | 108 | -0 | u2=10 | |
| -18 | 4155 | -4 | -0 | u3= 16 | |
| -3 | 752 | 14011 | 400 | u4= 13 | |
| vj | v1=4 | v2=-11 | v3=-2 | 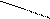 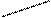 v4=-13 v4=-13 |
F ( 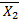 ) = 280∙4 + 340∙14 + 10∙8 + 415∙5 + 75∙2 + 140∙ll + 40∙0 = 9725
) = 280∙4 + 340∙14 + 10∙8 + 415∙5 + 75∙2 + 140∙ll + 40∙0 = 9725
5) Проверим план 
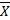 2 на оптимальность.
2 на оптимальность.
Оценим занятые клетки, дополним таблицу 19.
u1+v1=4 ] u1=0
u2+v1=14 v1=4
u2+v3=8 u2=10
u3+v2=5 v3= 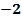
u4+v2=2 u4=13
u4+v3=11 v2= - 11
u4+v4=0 u3=16
v4= - 13
Оценим пустые клетки.
 12=17 – (0 - 11) = 28
12=17 – (0 - 11) = 28
 13=7 – (0- 2) = 9
13=7 – (0- 2) = 9
 14=0 – (0- 13) = 13
14=0 – (0- 13) = 13
 22= 20 – (10- 11) = 21
22= 20 – (10- 11) = 21
 24=0 - (10 - 13 )= 3
24=0 - (10 - 13 )= 3
 31=18– (16 + 4) = - 2
31=18– (16 + 4) = - 2
 33=4 – (16 - 2) = -10
33=4 – (16 - 2) = -10
 34=0- (16 - 13) = -3
34=0- (16 - 13) = -3
 44=3 – (13 +4) = - 14
44=3 – (13 +4) = - 14
Второй опорный план 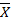 2 так же не является оптимальным, продолжаем его улучшать.
2 так же не является оптимальным, продолжаем его улучшать.
6) Перезагрузим «худшую» клетку (4,1).





 340 10 200 150
340 10 200 150
 +
+

 0 140 140 0
0 140 140 0
+ −
В результате получим новый опорный план 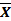 2 :
2 :
Табл. 20
 bj ai bj ai | ui | ||||
| 2804 | -17 | -7 | -0 | u1=0 | |
| 20014 | -20 | 1508 | -0 | u2=10 | |
| -18 | 4155 | -4 | -0 | u3= 3 | |
| 1403 | 752 | -11 | 400 | u4= - 1 | |
| vj | v1=4 | v2=3 | v3=-2 | 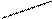 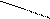 v4=1 v4=1 |
F ( 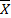 3) =280∙4 + 200∙14 + 150∙8 + 415∙5 + 140∙3 + 75∙2 + 40∙0 = 7765
3) =280∙4 + 200∙14 + 150∙8 + 415∙5 + 140∙3 + 75∙2 + 40∙0 = 7765
7) Проверим план 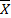 3 на оптимальность.
3 на оптимальность.
Оценим занятые клетки, дополним таблицу 20.
u1+v1=4 ] u1=0
u2+v1=14 v1=4
u2+v3=8 u2=10
u3+v2=5 v3= 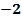
u4+v1=3 u4= - 1
u4+v2=2 v2= 3
u4+v4=0 u3=3
v4= 1
Оценим пустые клетки.
 12=17 – (0 +3) = 14
12=17 – (0 +3) = 14
 13=7 – (0- 2) = 9
13=7 – (0- 2) = 9
 14=0 – (0+1) = - 1
14=0 – (0+1) = - 1
 22= 20 – (10+3) = 7
22= 20 – (10+3) = 7
 24=0 - (10 +1 ) = - 11
24=0 - (10 +1 ) = - 11
 31=18– (3+ 4) = 11
31=18– (3+ 4) = 11
 33=4 – (3 - 2) = 3
33=4 – (3 - 2) = 3
 34=0- (3 +1) = - 4
34=0- (3 +1) = - 4
 44=3 – ( - 1 - 2) = 6
44=3 – ( - 1 - 2) = 6
План 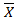 3 не является оптимальным.
3 не является оптимальным.
8) Перезагрузим клетку (2,4).





 200 0 160 40
200 0 160 40
 +
+

 140 40 180 0
140 40 180 0
+ −
Получим новый план 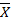 4.
4.
Табл. 21
 bj ai bj ai | ui | ||||
| 2804 | -17 | -7 | -0 | u1=0 | |
| 16014 | -20 | 1508 | 400 | u2=10 | |
| -18 | 4155 | -4 | -0 | u3= 2 | |
| 1803 | 752 | -11 | -0 | u4= - 1 | |
| vj | v1=4 | v2=3 | v3=-2 | 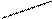 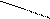 v4=-10 v4=-10 |
F ( 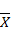 4) = 280∙4+160∙14 + 150∙8 + 40∙0+415∙5 + 180∙3 + 75∙2 = 7325
4) = 280∙4+160∙14 + 150∙8 + 40∙0+415∙5 + 180∙3 + 75∙2 = 7325
9) Проверим план 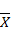 4 на оптимальность.
4 на оптимальность.
Для занятых клеток:
u1+v1=4 ] u1=0
u2+v1=14 v1=4
u2+v3=8 u2=10
u2+v4=0 v3= -2
u3+v2=5 v4= -10
u4+v1=3 u4= -1
u4+v2=2 v2=3
u3= 2
Для пустых клеток:
 12=17 – (0 +3) = 14
12=17 – (0 +3) = 14
 13=7 – (0- 2) = 9
13=7 – (0- 2) = 9
 14=0 – (0 - 10) = 10
14=0 – (0 - 10) = 10
 22= 20 – (10+3) = 7
22= 20 – (10+3) = 7
 31=18– (2+ 4) = 12
31=18– (2+ 4) = 12
 33=4 – (2 - 2) = 4
33=4 – (2 - 2) = 4
 34=0- (2 - 10) = 8
34=0- (2 - 10) = 8
 43=11- (- 1 - 2) = 14
43=11- (- 1 - 2) = 14
 44=0– (- 1 - 10) =11
44=0– (- 1 - 10) =11
Поскольку все оценки не отрицательны, то план оптимален.
 280 0 0
280 0 0
160 0 150
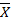 опт.= 0 415 0
опт.= 0 415 0
180 75 0
Fопт.( 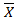 4) = 7325 тысяч рублей.
4) = 7325 тысяч рублей.
Анализ плана. Первому поставщику A1 следует весь товар отправить первому заказчику B1, второй поставщик А2 должен отправить 160 ед. товара первому заказчику B1 и 150 ед. товара - третьему заказчику В3, третий поставщик А 3 отправит весь товар заказчику В2, а четвертый поставщик А4 отправит 180 ед. товара заказчику B1 и 75 ед. товара - заказчику В2. При этом плане 40 ед. товара второго поставщика А2 остается нереализованным. Общая стоимость доставки товара заказчикам будет минимальной и составляет 7325 тысяч рублей.
Так как среди последних оценок - все строго положительные, то данный оптимальный план является единственным.
Замечание. Алгоритм и методы решения транспортной задачи могут быть использованы при решении многих экономических задач, не имеющих отношение к транспортировке грузов.
Контрольные задания.
Задание 1. Составить математическую модель задачи ЛП и решить её графическим способом.
1-10. Предприятие выпускает изделия двух видов. Для их изготовления используются три вида ресурсов. В наличии имеется bj (j=1,2,3) ресурсов. Расходы ресурсов на одно изделие каждой модели aij ,(i=1,2; j=1,2,3). Прибыль на одно изделие cj (j=1,2). Условия задачи можно кратко записать в виде следующей таблицы:
| Наименование изделия | Нормы на одно изделие | Прибыль на одно изделие | ||
| Рес.1 | Рес.2 | Рес.3 | ||
| Изделие A | a11 | a12 | a13 | c1 |
| Изделие B | a21 | a22 | a23 | c2 |
| Наличие ресурсов | b1 | b2 | b3 | - |
Требуется составить план выпуска изделий A и B, обеспечивающий максимальную прибыль.
| № вар. | a11 | a12 | a13 | a21 | a22 | a23 | b1 | b2 | b3 | c1 | c2 |
| 1. | 2,4 | 8,0 | 6,2 | 12,2 | 5,4 | 2,2 | |||||
| 2. | |||||||||||
| 3. | 10,0 | 14,0 | 3,6 | 20,0 | 7,4 | 12,4 | |||||
| 4. | 9,2 | 10,0 | 3,0 | 15,0 | 5,0 | 12,0 | |||||
| 5. | |||||||||||
| 6. | 10,0 | 14,0 | 3,8 | 22,0 | 7,5 | 14,5 | |||||
| 7. | |||||||||||
| 8. | 2,6 | 7,6 | 4,0 | 8,2 | 3,8 | 2,1 | |||||
| 9. | |||||||||||
| 10. | 2,2 | 8,4 | 4,2 | 8,2 | 4,6 | 2,0 |
11-20. На предприятии в процессе производства используется два технологических способа I и II. При этом расходуются сырьё, трудовые ресурсы и учитываются накладные расходы. Известны удельные затраты каждого ресурса aij (i=1,2; j=1,2,3), запасы ресурсов bj (j=1,2,3) и удельная прибыль cj (j=1,2) при использовании каждого технологического способа. Под удельными затратами и удельной прибылью понимают затраты и прибыль при единичной интенсивности соответствующего интенсивности технологического способа. Условия задачи можно кратко записать в виде таблицы:
| Виды ресурсов | Технологический способ | Запасы ресурсов | |
| I | II | ||
| Сырьё | a11 | a12 | b1 |
| Трудовые ресурсы | a21 | a22 | b2 |
| Накладные расходы | a31 | a32 | b3 |
| Прибыль | c1 | c2 | - |
Требуется составить план использования технологических способов в производстве, обеспечивающий максимальную прибыль.
| № вар. | a11 | a21 | a31 | a12 | a22 | a32 | b1 | b2 | b3 | c1 | c2 |
| 11. | |||||||||||
| 12. | |||||||||||
| 13. | |||||||||||
| 14. | |||||||||||
| 15. | |||||||||||
| 16. | |||||||||||
| 17. | |||||||||||
| 18. | |||||||||||
| 19. | |||||||||||
| 20. |
Задание 2. Для реализации трёх групп товаров коммерческое предприятие располагает тремя видами ограниченных материально-денежных ресурсов в количестве b1, b2, b3 за единицу. При этом для продажи 1 группы товаров на 1 тыс. руб. товарооборота расходуется ресурс первого вида в количестве a11 единиц, ресурс второго вида в количестве a21 единиц, ресурс третьего вида в количестве a31 единиц. Для продажи 2 и 3 групп товаров на 1 тыс. руб. товарооборота расходуется соответственно ресурса первого вида в количестве a12, a13 единиц, ресурсов второго вида в количестве a22, a23 единиц, ресурсов третьего вида в количестве a32, a33 единиц. Прибыль от продажи трёх групп товаров на 1 тыс. руб. товарооборота составляет соответственно c1, c2, c3 (тыс. руб.). Определить плановый объём и структуру товарооборота так, чтобы прибыль торгового предприятия была максимальной.
| № вар. | a11 | a12 | a13 | a21 | a22 | a23 | a31 | a32 | a33 | b1 | b2 | b3 | c1 | c2 | c3 |
| 1. | |||||||||||||||
| 2. | |||||||||||||||
| 3. | |||||||||||||||
| 4. | |||||||||||||||
| 5. | |||||||||||||||
| 6. | |||||||||||||||
| 7. | |||||||||||||||
| 8. | |||||||||||||||
| 9. | |||||||||||||||
| 10. | |||||||||||||||
| 11. | |||||||||||||||
| 12. | |||||||||||||||
| 13. | |||||||||||||||
| 14. | |||||||||||||||
| 15. | |||||||||||||||
| 16. | |||||||||||||||
| 17. | |||||||||||||||
| 18. | |||||||||||||||
| 19. | |||||||||||||||
| 20. |
Задачу решить симплекс-методом.
Задание 3. Используя условия предыдущей задачи, необходимо:
а) К прямой задачи планирования товарооборота составить двойственную задачу ЛП;
б) Установить сопряжённые пары переменных прямой и двойственной задач;
в) Согласно сопряжённым парам переменных из решения прямой задачи, в которой производится оценка ресурсов, затраченных на продажу товаров.
Задание 4. Поставщики товара – оптовые коммерческие предприятия A1, A2, A3 имеют запасы товаров в количестве a1, a2, a3 единиц и розничные торговые предприятия B1, B2, B3 подали заявки на закупку товаров в объёмах соответственно b1, b2, b3. Тарифы перевозок единицы груза из каждого пункта поставок в соответствующие пункты потребления заданы в таблице. Требуется найти такой план перевозки груза от поставщиков к потребителям, чтобы совокупные затраты на перевозку были минимальными.
| bj ai | |||
| bj ai | |||
| bj ai | |||
1. 2.
| bj ai | |||
3. 4.
| bj ai | |||
| bj ai | |||
| bj ai | |||
5. 6.
| bj ai | |||
| bj ai | |||
| bj ai | |||
7. 8.
9. 10.
11. 12.
| bj ai | |||
| bj ai | |||
| bj ai | |||
| bj ai | |||
| bj ai | |||
| bj ai | |||
| bj ai | |||
| bj ai | |||
| bj ai | |||
| bj ai | |||
13. 14.
15. 16.
17. 18.
19. 20.
Контрольные вопросы.
1. Что называется математической моделью экономической задачи оптимизации?
2. Какой вид имеет математическая модель задачи линейного программирования?
3. Какая задача ЛП называется стандартной?
4. Какая задача ЛП называется канонической?
5. Что такое допустимое решение задачи ЛП?
6. Что образует область допустимых решений?
7. Какой план называется оптимальным?
8. Какой существует порядок составления математической модели задачи ЛП?
9. Какие задачи ЛП можно решать графическим методом?
10. Какой существует порядок решения задачи ЛП графическим методом?
11. Как строится вектор 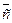 и что он определяет?
и что он определяет?
12. Как находится экстремальное значение целевой функции при решении задачи ЛП графическим методом?
13. Как найти точное решение задачи ЛП при графическом решении?
14. В чём состоит идея решения задачи симплексным методом?
15. Каков порядок решения задачи симплексным методом?
16. Как строится первый опорный план?
17. Как проверяется план на оптимальность?
18. Как строится новый опорный план?
19. Как формулируется пара симметричных двойственных задач?
20. Какова связь между формулировками прямой и двойственной задач?
21. Какова связь между решениями прямой и двойственной задач?
22. Как по решению прямой задачи найти решение двойственной задачи?
23. Как формулируется транспортная задача по критерию стоимости?
24. Что такое открытая и закрытая модель транспортной задачи?
25. Какова структура распределительной таблицы?
26. Как построить исходный план перевозок по правилу северо-западного угла?
27. Как построить исходный план перевозок по методу минимальной стоимости?
28. Как оценить построенный план перевозок?
29. Каков порядок решения задачи методом потенциалов?
30. Что такое цикл в транспортной задаче?
31. Как определить единственность транспортной задачи?
Содержание:
I. Пояснительная записка. Целевая установка……1
II. Программа…………………………………………...2
III. Рекомендуемая литература………………………..2
IV. Методические указания……………………………3
Тема 1. Общее линейное программирование(ЛП)….3
1.1 Основные понятия и определения……………3
1.2 Примеры задач ЛП…………………………….5
Тема 2. Графический метод решения задач ЛП...…15
2.1 Геометрическая интерпретация задачи ЛП...15
2.2 Алгоритм решения задачи ЛП графическим
методом……………………………………….16
2.3 Примеры решения задачи ЛП графическим
методом……………………………………….17
2.4 Пример решения экономической задачи
графическим методом………………………..20
Тема 3. Симплекс – метод решения задачи ЛП……22
3.1 Алгоритм симплексного метода ………...…23
3.2 Пример решения задачи ЛП
симплекс – методом…………………….…...25
3.3 Частные случаи решения задачи ЛП
симплекс – методом…………………………29
Тема 4. Двойственная задача ЛП……………………30
4.1 Математическая модель двойственной
задачи ЛП………………………………….…30
4.2 Соотношения между прямой и двойственной
задачами ЛП…………………………………31
4.3 Пример решения двойственной задачи ЛП..32
Тема 5.Транспортная задача…………………………….33
5.1 Математическая модель транспортной задачи.33
5.2 Нахождение исходного опорного плана……....35
5.3 Проверка решения на оптимальность …...……36
5.4 Переход от одного опорного решения к другому37
5.5 Пример решения транспортной задачи………..38
Контрольные задания……………………………………..48
Контрольные вопросы…………………………………....54
