Модель потока ошибок в дискретном канале связи без памяти

Если ошибки независимы, тогда различные сочетания ошибок кратности r имеют вероятность

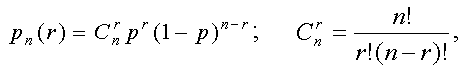
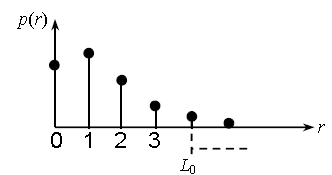
Вероятность того, что будут ошибки кратности r > L₀, описываетсяформулой

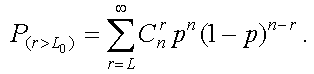
Существует два состояния для канала связи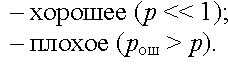

35 Напишите о независимых ошибках

Для характеристики независимых ошибок часто используется пуассоновская модель (p << 1).

Вероятность r-кратных ошибок

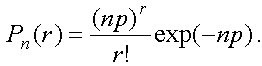
36 Приведите требования к определению количества информации

Требования к определению количества информации:

– количество информации должно быть аддитивной мерой;

– количество информации о достоверном событии равно нулю;

– количество информации не должно зависеть от содержания.

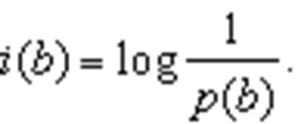
37 Приведите свойства энтропии

Для характеристики всего ансамбля сообщений используется энтропия:

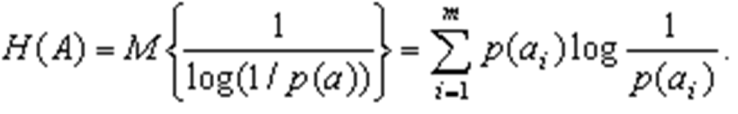
Энтропия является основной характеристикой источника сообщений.

Свойства энтропии

1. Энтропия неотрицательна: H(A) = 0;

p(a_i) = 1;p(a_j) = 0.

2. Энтропия аддитивна, т. е. если (a1, a2, …,an), то H(А, А, …, А) = nH(A).

3. Если в ансамбле K = mⁿ различных сообщений, то H(A) ≤ log K.

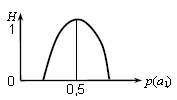
Зависимость

энтропии от вероятности

состояния для системы

из двух состояний

38 Напишите при каких условиях используется условная информация

Условная взаимная информация — статистическая функция трёх случайных величин, описывающая количество информации, содержащееся в одной случайной величине относительно другой, при условии заданного значения третьей:

39 Напишите формулу энтропии

Для характеристики всего ансамбля сообщений используется энтропия:

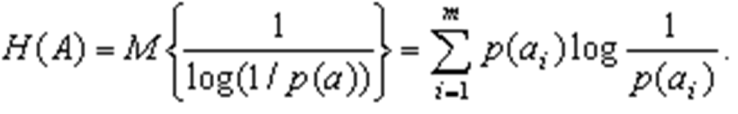
Энтропия является основной характеристикой источника сообщений.

Свойства энтропии

2. Энтропия неотрицательна: H(A) = 0;

p(a_i) = 1;p(a_j) = 0.

2. Энтропия аддитивна, т. е. если (a1, a2, …,an), то H(А, А, …, А) = nH(A).

3. Если в ансамбле K = mⁿ различных сообщений, то H(A) ≤ log K.

Зависимость

энтропии от вероятности

состояния для системы

из двух состояний

40 Определите энтропию равновероятных статистически независимых букв

Например, в русском или казахском языке вероятность появления в сообщении буквы зависит от того, какие буквы стоят на других местах. Наличие статистических связей между буквами уменьшает энтропию на букву и число сообщений.

1) если буквы независимы, то H(A₁, A₂) = H(A₁) + H(A₂) и энтропия на букву

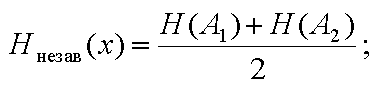
41 Напишите о радиосвязи прямой видимости

LPD радиостанции работают в диапазоне УКВ (433 МГц) и имеют невысокую мощность передатчика. Распространение ультракоротких волн (УКВ) имеет одну специфическую особенность: они распространяются только прямолинейно. Они не могут огибать земную поверхность, как длинные (ДВ) и средние (СВ) волны, и отражаться от ионосферы, как короткие (KB), поэтому радиосвязь на УКВ возможна только в пределах прямой видимости. Для определения потенциальной дальности радиосвязи на УКВ без учета энергетики (чуствительность приемника, мощность передатчика, потери энергии на трассе) обратимся к простым геометрическим расчетам (см. рис.1).

Рис.1 Расчет зоны прямой видимости над поверхностью земли. H1, H2 - высоты поднятия антенн над поверхностью земли, L - потенциальная дальность прямой видимости, R - радиус земли.

42 Напишите формулу энтропии статистически зависимых символов

Статистически зависимые символы.Например, в русском или казахском языке вероятность появления в сообщении буквы зависит от того, какие буквы стоят на других местах. Наличие статистических связей между буквами уменьшает энтропию на букву и число сообщений. Если учитывать зависимость только двух соседних букв, то для сообщения длиной N

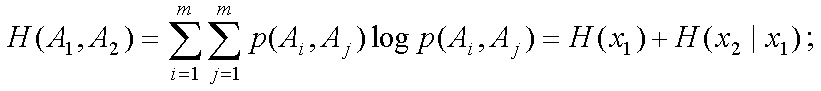
43 Приведите формулы избыточности и производительности источника

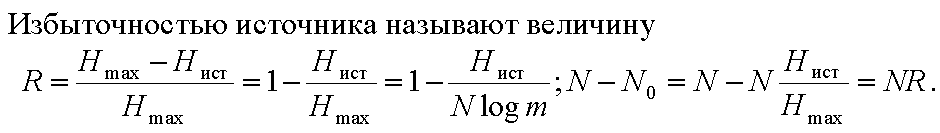
Производительностью источника называют среднее количество информации, выдаваемой источником в единицу времени [бит/с]:

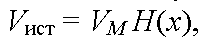
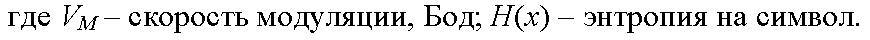
44 Напишите о информации в сложной системе

Рассмотрим сложную систему (X, Y), где X и Y – две статистически зависимые случайные величины.

Над величиной Y проводится опыт, на основании которого снижается неопределённость относительно значения X. Количество информации относительно X, получаемое из опыта над случайной величиной Y, определяется как уменьшение исходной неопределённости

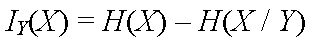
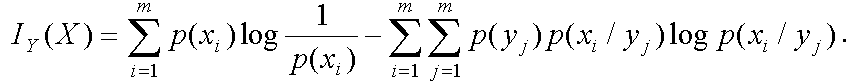
45 Напишите формулу средней длины кодовой группы