Тепловой поток. Коэффициент теплопроводности
Пусть в среде имеют место различные значения температуры, т. е. имеется градиент температуры, тогда в этой среде будет существовать тепловой поток (распространение теплоты). Тепловой поток направлен в сторону убывания температуры. Линии теплового потока совпадают с линиями максимальных градиентов лишь в изотропных телах, где они создают с изотермами криволинейную, но ортогональную сетку.
Французский ученый Фурье, изучая перенос теплоты в средах, открыл эмпирический закон, согласно которому удельный тепловой поток (или интенсивность теплового потока) прямо пропорционален градиенту температуры:
q = λ (- ¶t/¶n), (3.9)
где λ — коэффициент пропорциональности; n — нормаль к изотермической поверхности.
Формула (3.9) в настоящее время носит название закона Фурье. Коэффициент пропорциональности λ называют коэффициентом теплопроводности. Для получения положительного значения теплового потока в уравнении (3.9) необходимо ставить знак минус.
Зная удельный тепловой поток, можем определить тепловой поток, проходящий через некоторую площадь F, выделенную на изотермической поверхности:
Q = qF = - λ ¶t/¶n F.(3.10)
Теплопроводность вещества, в частности воды и льда, имеет исключительное значение в природе. Благодаря теплопроводности (передаче теплоты) происходит выравнивание температуры в теле или среде. В твердых телах передача теплоты (теплопередача) осуществляется от молекулы к молекуле вследствие их соприкосновения. Для твердых тел она является единственно возможной и называют ее кондукцией, касанием или молекулярной. В жидких средах молекулярная теплопередача играет существенную роль только в том случае, если жидкость находится в покое. Для жидкостей, в том числе и для воды, характерно существование еще двух видов теплопередачи, обусловленных турбулентностью потока и конвекцией.
Характеристикой молекулярной теплопередачи является коэффициент теплопроводности λ. Он является физическим параметром вещества и зависит от его структуры, плотности, влажности, температуры и давления. Коэффициент теплопроводности определяется опытным путем с использованием уравнения (3.10), которое можно представить в виде
λ = -Q/[Fτ Δt/(Δn)], (3.11)
где τ — время.
Численно коэффициент теплопроводности равен количеству теплоты, которая проходит через 1 м2 изотермической поверхности в 1 ч при слое вещества в 1 м и разности температуры на границах слоя в 1°С.
По теплопроводности материалы подразделяются на твердые тела, газы и жидкости.
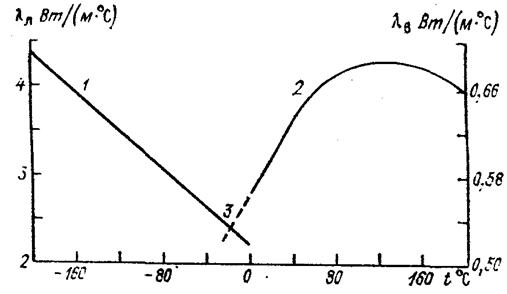
Рис. 3.2. Зависимость коэффициента теплопроводности от температуры [8]
1 — лед; 2 и 3 — вода и переохлажденная вода.
Коэффициент теплопроводности твердых тел составляет 20—400 Вт/(м·°С) (металлы) и 0,02—3,00 Вт/(м·°С) (строительные материалы), газов — 0,005—0,500 Вт/(м·°С) и жидкостей 0,08—0,70 Вт/(м·°С).
Коэффициент теплопроводности большинства жидкостей с повышением температуры убывает. Вода в этом отношении является исключением. С увеличением температуры от 0 до 127°С коэффициент теплопроводности воды увеличивается, а при дальнейшем возрастании температуры — уменьшается (рис. 3.2). При 0°С коэффициент теплопроводности воды равен 0,569 Вт/(м·°С). С увеличением минерализации воды коэффициент ее теплопроводности уменьшается, но очень незначительно.
Давление оказывает влияние на теплопроводность жидкости, однако, в большей степени на теплопроводность газов. У воды теплопроводность при изменении давления в больших пределах практически не меняется. Это связано с малой сжимаемостью воды, которая определяется характером сил межмолекулярного взаимодействия.
Как вода среди жидкостей, так и лед среди твердых материалов являются исключением по проводимости теплоты. С повышением температуры коэффициент теплопроводности пресноводного льда не повышается, а понижается, достигая при 0°С 2,24 Вт/(м·°С) (рис. 3.2). Эта связь близка к линейной и может быть выражена, по данным Якоба и Эрка, эмпирической формулой
λл = 2,24 (1-0,0048t), (3.13)
где t — температура льда с учетом знака, °С.
Теплопроводность соленого льда уменьшается с ростом его солености, но увеличивается с понижением температуры, так как при этом возрастает концентрация рассола во льду.
Для ледяного покрова озер и рек характерно распределение коэффициента теплопроводности по его толщине. Это обусловлено более высокой температурой льда в нижних слоях (на нижней границе 0°С) и низкой температурой в расположенных выше слоях, а также пористостью, которая в верхних слоях больше, чем в нижних.
