Порядок выполнения работы. Задание 1.Определение коэффициента жесткости пружин

Задание 1.Определение коэффициента жесткости пружин

1. Укрепить на пружине груз массой m. Отклонить строго вертикально вниз груз от положения равновесия, растягивая пружину на 3 - 4 см и отпустить.

2. Найти время 8 - 20 полных колебаний и вычислить период Т. Аналогичные измерения и вычисления провести, укрепляя на пружине грузы разной массы (не менее 5). Заполнить таблицу 1.

Таблица 1.Определение коэффициента жесткости пружин

№	m, кг	n	t1, с	t2, с	t3, с	t4, с	t5, с	T, с	k, Н/м	Δk, Н/м	εk, %
1.
2.
3.
4.
5.
ср. зн.

3. По полученным данным построить график зависимости Т² = f(m) и определить коэффициент жесткости (по графику):

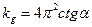(13)

где α – угол наклона графика к оси абсцисс (δm). Для определения ctgα на графике Т²(m) взять две произвольные точки, тогда

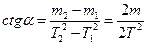(14)

коэффициент жесткости может быть определен из углового коэффициента прямой Т² (m), где m₁, m₂, T₁², T₂² - соответствующие координаты принятых точек.

4. Рассчитать погрешности.

5. Заполнить таблицу 1 и ответ записать в виде: .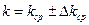

Задание 2.Определение коэффициента затухания

1. Отклонить строго вертикально вниз груз массой 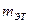от положения равновесия, растягивая пружину на 3 - 5 см.

2. Записать в таблицу 2 значение А₀.

3. Считают число колебаний (полных – n), дождаться значительного уменьшения амплитуды А (не менее, чем в 2 раза).

4. Записать в таблицу 2 значение числа совершенных колебаний n и значение амплитуды А_n.

5. По формуле (12) рассчитать значение β.

6. Проделать пункты 1-5 не менее 5 раз, изменяя значение А_n и n.

7. Рассчитать ошибки измерений.

Таблица 2.Определение коэффициента затухания

№	А0,м	n	An,м	t,c	β,1/с	Δ β	Еβ
Среднее значение

Контрольные вопросы:

1. Дать определение физических величин, характеризующих колебательное движение.

2. Получить дифференциальное уравнения незатухающих колебаний пружинного маятника.

3. Уравнения свободных незатухающих колебаний (дифференциальное уравнение и его решение).

4. Величины, характеризующие колебания: амплитуда, частота и циклическая частота, фаза и начальная фаза.

5. Что характеризует коэффициент затухания.

6. Нарисуйте графики различных видов затухания.

7.Пружинный маятник. Способы определения в данной работе: коэффициента жесткости пружины, периода колебаний маятника, коэффициента затухания, логарифмического декремента затухания.

Лабораторная работа № 1-4

Определение момента инерции тел методом крутильных колебаний

Цель работы: определить моменты инерции тел правильной формы и их прочностных характеристик, с использованием крутильных колебаний.

Оборудование:

1. Устройство для получения крутильных колебаний;

2. Набор тел различной правильной формы;

3. Масштабная линейка;

4. Микрометр или штангенциркуль;

5. Секундомер.

КРАТКАЯ ТЕОРИЯ

Моментом инерции материальной точки относительно какой-либо оси называется произведение ее массы на квадрат расстояния до этой оси:

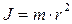(1)

Моментом инерции твердого телаотносительно какой либоосиназывается сумма моментов инерции всех точек тела относительно этой же оси:

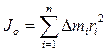(2)

Момент инерции тела относительно данной оси, не зависит от характера движения тела, а зависит от массы тела, его размеров, формы, т.е. от распределения массы относительно оси вращения. Момент инерции тел правильной геометрической формы может быть вычислен теоретически. Момент инерции тела является физической величиной, характеризующей инертность тела при вращательном движении: тело с большим моментом инерции будет иметь меньшее угловое ускорение при том же действующем моменте сил.

Расчет момента инерции тел. В формуле (2) элементарная масса 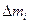, равна произведению плотности тела 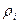в данной точке на соответствующий элементарный объем 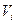: 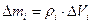. Следовательно, момент инерции можно представить в виде:

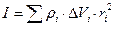(3)

Если плотность тела постоянная, ее можно вывести за знак суммы:

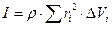(4)

Для сплошного тела соотношения (3) и (4) являются приближенными, причем тем более точными, чем меньше элементарные объемы 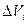и соответствующие им элементарные массы 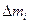. Следовательно, задача нахождения моментов инерции сводится к интегрированию:

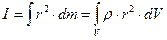(5)

Причем интеграл берется по всему объему, а величины r и r являются функциямикоординат. В качестве примера найдем момент инерции однородного шара (рис. 1).

Рис. 1.

Схематическое изображение однородного шара (R – радиус шара, r – радиус бесконечно малого элемента, z – расстояние)

При вычислении момента инерции шара его разбивают на бесконечно большое число бесконечно малых элементов с массами dm (см. рис. 1), тогда масса шара равна:

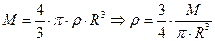(6)

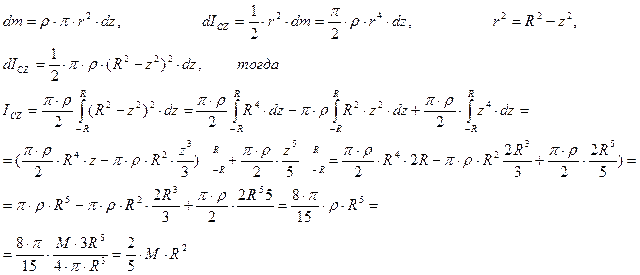
Момент инерции шара равен:

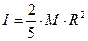(7)

Формулы для расчета момента инерции тел правильной формы массы m относительно осей, проходящих через центр масс даны в таблице 1.

Если же тело имеет сложную форму (маховое колесо, коленчатый вал, винт и т.д.), то теоретически определить момент инерции трудно. В таких случаях момент инерции определяют экспериментальным путем, например, используя крутильные колебания.

Таблица 1.Таблица моментов инерции для однородных тел простейшей формы

№ п.п.	Тело	Положение оси OZ	Момент инерции I
	Полый тонкостенный цилиндр радиусом R и массой m.	Ось симметрии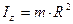
	Сплошной цилиндр (диск) радиусом R и массой m.	Ось симметрии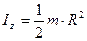
	Прямой тонкий стержень длиной l и массой m.	Ось перпендикулярная стержню и проходит через его середину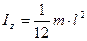
	Прямой тонкий стержень длиной l и массой m.	Ось перпендикулярная стержню и проходит через его конец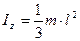
	Шар радиусом R и массой m.	Ось проходит через центр шара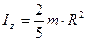
	Шар радиусом R и массой m.	Ось проходит на расстоянии d от центра шара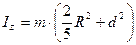

Схема крутильного маятника изображена на рис. 2

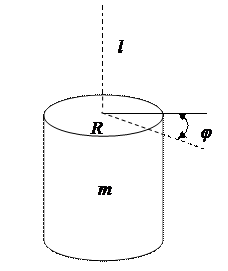
Рис. 2

Схема крутильного маятника: (R – радиус цилиндра, l – длина проволоки, φ – уголповорота)

Крутильный маятник представляет собой упругую проволоку с закрепленным верхним концом к нижнему концу, которой жестко присоединено изучаемое тело.

Поворачивая тело на угол j, мы создаем в проволоке возвращающий момент упругой силы М_уп, который по закону Гука пропорционален деформации кручения j

Мупр= -¦j

(8)

где ¦ - модуль кручения, который зависит от параметров проволоки.

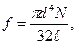(9)

где d - диаметр проволоки; l - длина проволоки; N - модуль сдвига материала проволоки.

По второму закону Ньютона, момент упругой силы создает угловое ускорение 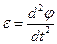пропорциональное этому моменту.

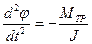(10)

Таким образом, свободное вращение крутильногомаятника при пренебрежении силами трения, будет описываться дифференциальными уравнениями, объединяющими второй закон Ньютона и закон Гука.

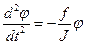(11)

Интегрируя эти уравнения, получаем его решение

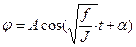(12)

Следовательно, при допустимости сделанныхнами упрощений, маятникбудет совершать гармонические колебания с периодом колебаний

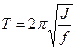(13)