Линейное программирование

1. Задачи линейного программирования и их свойства

Во многих областях практики возникают своеобразные задачи исследования операций отмеченными особенностями:

· показатель эффективности W есть линейная функция от элементарного решения ;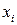

· ограничительное условие, полагаемая на элементарные решения имеют вид линейных равенств или неравенств. Такие задачи являются задачами линейного программирования.

Запишем формулировки основных задач линейного программирования.

Задача о пищевом рационе:

Сельхоз предприятия производит откорм скота с коммерческой целью. Иметься 4 вида продуктов питания 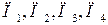. Стоимость ед. продукта соответственно равна 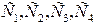. Требуется составить пищевой рацион, который должен содержать:

· белков, не менее 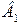единиц;

· углеводов, не менее 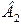единиц;

· жиров, не менее 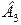единиц.

Для продуктов 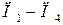содержание жиров, белков, углеводов приведены в таблице:

Продукты	Элементы
Белки	Углеводы	Жиры

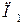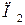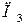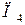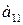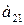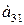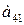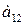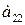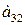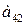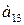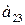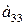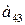Пищевой рацион состоит таким образом что бы его стоимость была минимальной.

Решение:

1. Составить математическую модель:

Пусть 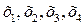- количество продуктов 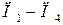, входящих в рацион. Тогда стоимость рационального питания (показатель эффективности) равен:

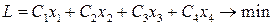
Запишем ограничения по белкам, углеводам и жирам

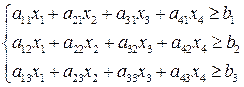
Ограниченное количество элементов. Поставлена задача сводится к тому чтобы найти 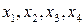при которому себестоимость рационализации была минимальная.

Задача о загрузке оборудования

Каждая ткацкая фабрика имеет в наличии 2 вида станков; среди них 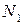- станков типа І, 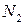- станков II типа. Станки производят 3 типа тканей 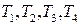, но с разной производительностью. Станок типа І производит в месяц 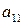метров ткани 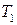, 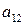метров ткани 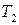, 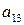метров ткани 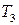. Можно составить таблицу для 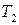и

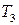
Станок	Тип ткани
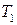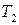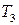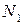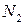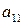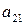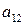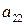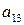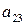Прибыль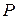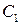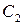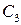

Фабрикой приписан план производительности за месяц метров ткани 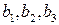. Требуется так распределить загрузку станков что бы план был выполнен, станки не простаивали и суммарная прибыль была максимальная.

Решения:

Математическая модель такой задачи:

Пусть 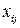- число станков типа 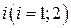занятых производством ткани 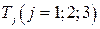. Таким образом получаем 6 переменных 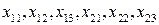(необходимо выбрать таким образом, что бы прибыль была максимальной)

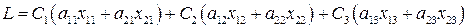
Станки не должны простаивать, поэтому

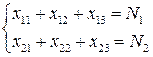
Кроме того, должны быть выполнено задание по ассортименту с учетом производительности станков

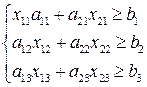
Поставленная задача сводиться к тому, что бы получить такие неотрицательные значения переменных 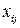удовлетворяющие ограниченные условием по загрузке и ассортименту, а целевая функция обращалась в максимум.

Задача о перевозках

Имеется 4 пункта отправления: 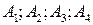в которых сосредоточенные запасы определенного вида груза в количествах 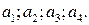Кроме того, имеется 3 пункта назначения 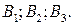Пункты подали заявки на 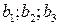единиц груза. Сума заявок равна суме имеющихся запасов, 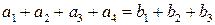. Известна стоимость перевозки груза из пункта А в пункт В. Стоимость каждой перевозки будет начисляться: ;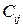

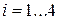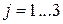
Требуется составить такой план перевозок (какое количество груза откуда и куда отправить) при котором суммарные перевозки обращаются в минимум.

Математическая модель задачи:

Пусть 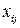- количество единиц груза отправляемого из 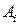пункта в 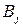пункт назначения.

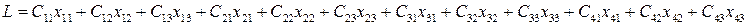Запишем ограничения налягаемые на элементы решения. Ограничения записываем с учетом того, что все заявки должны быть выполнены.

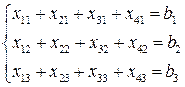
Так, как все запасы должны быть исчерпаны, то:

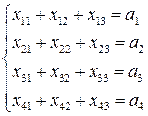
Требуется выбрать такие неотрицательные значения переменных 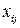что бы выполнялись все заданные выше ограничения и при этом целевая функция обращалась в минимум. Основными особенностями ограничительных условий записанных в задаче является то, что в первуй задаче ограничения имели вид линейных неравенств, во второй – линейных неравенств и равенств, а в третей – только равенств.

Однако любую задачу линейного программирования с условиями - неравенства можно свести к задаче с условными равенствами путем введения остаточных или избыточных переменных.

Формула записи задачи ЛП, которая ограниченная только равенствами называется стандартной формой, а сама задача называется задачей ЛП (ОЗЛП).

Симплекс метод

Графический способ решения задач линейным программированием показывает, что оптимальное решение всегда осоциируется с угловой точкой пространственных решений. В математике она называется крайней точкой множества. Этот метод является ключевой идеей при разработке общего алгебраического симплекс метода применяемого для любого решения задачи ЛП.

Переход от геометрического способа решения задач ЛП к симплекс методу лежит через алгебраическое описание крайних точек пространства допустимых решений. Для реализации этого перехода сначала необходимо привести задачу ЛП к стандартной форме, преобразовав неравенство ограничений в равенство, путем введения дополнительных введений.

Стандартная форма записи задач ЛП необходима, потому что она позволяет получить базисное решение (это решение, которое полностью определяет все геометрические крайние точки пространства допустимых решений).

Симплекс метод позволяет эффективно найти оптимальное решение среди всех базисных. Стандартная форма записи задач ЛП предполагает выполнение следующих требований:

· все ограничения преобразовываются в равенства с неотрицательной правой частью;

· все переменные неотрицательные;

· целевую функцию нужно либо максимизировать либо минимизировать.

Преобразование неравенства в равенства

Неравенства любого типа можно преобразовать в равенства путем добавления в левую часть дополнительных переменных – остаточных либо избыточных.

Пример 1:

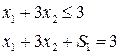
- остаточная переменная

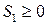
Пример 2:

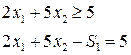
Преобразование свободных переменных в неотрицательные:

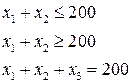
Свободную переменную, которая может быть больше нуля, либо меньше нуля, можно представить как разницу двух неотрицательных переменных

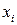
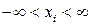
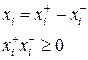
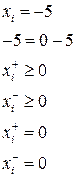
Преобразование задачи максимизации в задачу минимизации. Задача максимизации функции эквивалентна задачи минимизации, поскольку при решении обеих задач представлен один и тот же набор значений переменных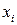

Редимикс

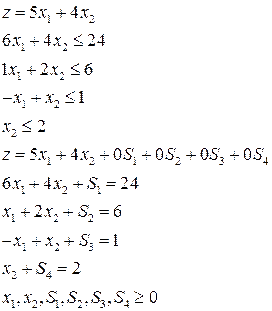
Задачу ЛП в стандартной форме можно представить в виде следующей таблицы (симплекс таблицы)

Базис		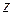		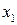		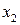		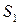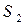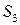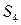Решения
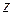		-5	-4
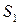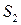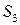		-1							-1

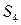Для решения задачи симплекс методом лежит 2 условия

Условие оптимальности – вводимой переменной в задачи максимизации (минимизации является небазисная переменная имеющая наибольший отряд (положительный) коэффициент в z – строке.

Если в z строке есть несколько таких коэффициентов, то выбор вводимой переменной делается произвольно.

Оптимальное решение достигнуто, когда в z строке все коэффициенты при небазисных переменных будут неотрицательны (неположительны).

Условие допустимости – как в задаче максимизации, так и в задаче минимизации, в качестве исключаемых выбирается базисная переменная, для которой отношение значения к положительному коэффициенту ведущего столбца – минимально.

Если базисных переменных с такими свойствами несколько, то выбирается один из них произвольно:

Базис		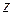		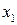		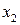		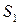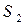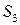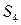Решения
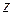		-5	-4
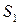	0/6		2/3	1/5
	-	-	-	-	-	-	-	-
	-	-	-	-	-	-	-	-
	-	-	-	-	-	-	-	-

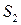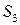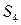Базис		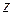		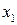		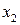		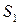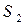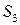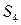Решения
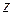			-2/3	5/6
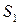			2/3	1/6
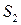			4/3	-1/6
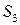	-		5/3	-	-	-	-
	-		-	-	-	-	-	-

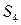Базис		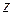		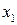		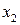		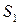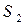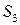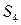Решения
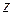		-5	-4						-
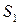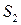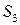		-1							-1

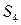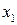вводим в базис 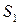выводим

Базис		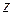		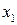		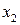		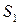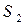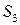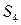Решения
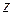			-2/3	5/6					-
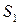			2/3	1/6
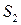			4/3	-1/6					3/2
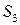			5/3	1/6

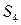Опять выбираем ведущую строку, теперь это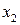

Базис		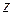		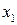		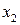		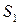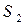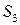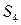Решения
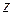				9/12	1/2
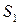				¼	-1/2
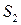				-1/8	5/4			3/2
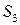				9/24	-5/4			5/2
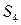				1/8	-3/4			½

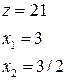
При использовании симплекс – метода могут встречаться особые случаи: вырожденность, альтернативные оптимальные решения, неограниченные решения отсутствие допустимых решений.

Вырожденность

В ходе выполнения симплекс – метода проверка условия допустимости может привести к неоднозначному выбору переменных. С практики вырожденность объясняется тем, что в исходной задаче есть хотя бы одно избыточное ограничение. При этом может наблюдаться неизменность значений всех переменных и целевой функции.