Кирхгофтың екінші заңы бойынша 3 страница
Жиіліктері бірдей екі синусоиданың басты фазаларының айырымы фазалық ығысу деп аталады. Бұл жағдайда фазалық ығысу кернеумен тоқтың арасында нөлге тең:
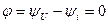 (2.13)
(2.13)
Кедергі 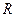 арқылы синусоидалды тоқ өткен кезде амплитуталар және кернеудің, тоқтың әрекетті мәндері Ом заңымен байланысқан, яғни
арқылы синусоидалды тоқ өткен кезде амплитуталар және кернеудің, тоқтың әрекетті мәндері Ом заңымен байланысқан, яғни
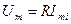 ;
; 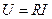
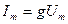 ;
; 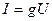 (2.14)
(2.14)
Кедергіге түсетін лезді қуат:
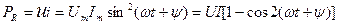 ,тоқтың және кернеудің жиілігіне қарағанда екі есе бұрыштық жиілікпен өзгереді. Тербелiну шектері 0-ден
,тоқтың және кернеудің жиілігіне қарағанда екі есе бұрыштық жиілікпен өзгереді. Тербелiну шектері 0-ден  -ге дейін (2.3 -сурет.)
-ге дейін (2.3 -сурет.)
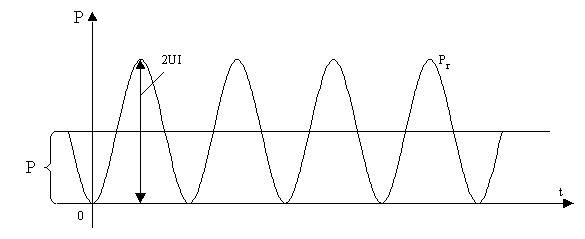
2.3 –сурет. Кедергіге түсетін лезді қуат 
PR қисығы екі қосындылардан құралады: тұрақты қосынды P=UI және амплитудасы UI, ал жиілігі 2 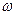 тең косинусойдалды функциядан.
тең косинусойдалды функциядан.
Период ішіндегі орташа қуаттың мәні активтік қуат деп аталады да, ол тең: 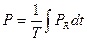 (ваттпен өлшенеді).
(ваттпен өлшенеді).
Қаралып отырған жағдайда 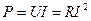 .
.
Кедергіні активтік қуаттың тоқтың шарашы шамасына қатынасы деп белгілеуге болады 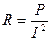 .
.
Айнымалы тоқ кездегі активтік кедергі деп аталады.
2.4 Индуктивтіктегі синусоидалды тоқ
Егер де L индуктивтік арқылы синусоидалды тоқ 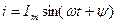 өтсе, онда өздік индукцияның электр қозғаушы күш тең:
өтсе, онда өздік индукцияның электр қозғаушы күш тең:
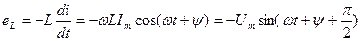 (2.16)
(2.16)
Демек, индуктивтіктегі кернеу:
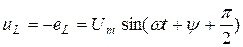 (2.17)
(2.17)
(2.17) кейіптемеден шығады: индуктивтіктегі кернеу тоқты 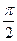 (немесе 90°) бұрышқа озып отырады; кернеудің максимумы тоқтың максимумынан солға қарай 90°-қа ығысады (2.4-сурет).
(немесе 90°) бұрышқа озып отырады; кернеудің максимумы тоқтың максимумынан солға қарай 90°-қа ығысады (2.4-сурет).


2.4-сурет. Индуктивтіктегі синусоидалы кернеу және тоқ
Фазалық ығысу:
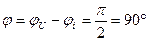 (2.18)
(2.18)
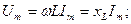
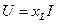 (2.19)
(2.19)
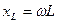 - индуктивтік кедергі, ал оған кері шама
- индуктивтік кедергі, ал оған кері шама 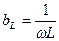 - индуктивтік өткізгіштік деп аталады. Сонымен,
- индуктивтік өткізгіштік деп аталады. Сонымен, 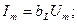
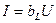 (2.20)
(2.20)
Индуктивтіктегі лезді қуат тең:
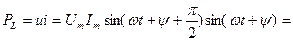
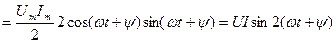 (2.21)
(2.21)
Бұл қуат амплитудасы 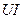 , ал бұрыштық жиілігі
, ал бұрыштық жиілігі 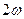 тең синусоидалды заң бойынша тербеленеді.
тең синусоидалды заң бойынша тербеленеді.
Индуктивтіктің магнит өрісінің энергиясы:
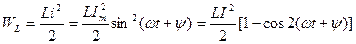 (2.22)
(2.22)
0 ден 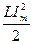 -ге дейін шектерде бұрыштық жиілігі
-ге дейін шектерде бұрыштық жиілігі 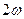 -мен периодикалы өзгеріп тұрады (2.5-сурет).
-мен периодикалы өзгеріп тұрады (2.5-сурет).


2.5-сурет. Индуктивтіктегі лезді қуат және өрістің энергиясы.
Көзбен және индуктивтіктің арасында энергияның тербелісі өтеді, ал индуктивтікке түсетін активтік қуат нөлге тең. Индуктивтік кедергіні былай табуға болады: 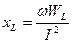 (2.23)
(2.23)
2.5 Сыйымдылықтағы синусойдалы тоқ
Егер де 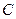 сыйымдылықтағы кернеу синусойдалды болса (2.6-сурет)
сыйымдылықтағы кернеу синусойдалды болса (2.6-сурет)
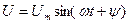 , онда тоқ:
, онда тоқ:
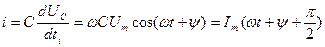 (2.24)
(2.24)
(2.24) көрініс көрсетіп тұр: тоқ 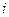 ынта салынған кернеуден
ынта салынған кернеуден 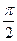 бұрышқа озып тұр, яғни тоқтың нөлдік мәніне кернеудің максималды мәні сәйкес.
бұрышқа озып тұр, яғни тоқтың нөлдік мәніне кернеудің максималды мәні сәйкес.


2.6-сурет. Сыйымдылықтағы синусойдалы кернеу және тоқ.
Фазалық ығысу: 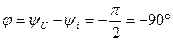 (2.25)
(2.25)
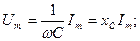
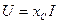 (2.26)
(2.26)
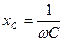 -сыйымдылық кедергі, ал оған кері шама
-сыйымдылық кедергі, ал оған кері шама 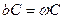 -сыйымдылық өткізгіштік деп аталады. Сонымен,
-сыйымдылық өткізгіштік деп аталады. Сонымен, 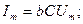
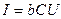 (2.27)
(2.27)
Сыйымдылықтағы лезді қуат:
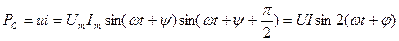 (2.28)
(2.28)
Бұл қуат амплитудасы 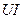 , ал бұрыштық жиілігі
, ал бұрыштық жиілігі 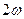 тең синусойдалды заң бойынша тербеленеді, яғни көрініс
тең синусойдалды заң бойынша тербеленеді, яғни көрініс 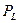 сияқты.
сияқты.
Сыйымдылықтың электр өрісінің энергиясы:
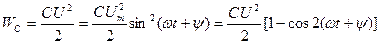 (2.29)
(2.29)
0-ден 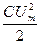 -ге дейін шектерде бұрыштық жиілігі
-ге дейін шектерде бұрыштық жиілігі 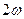 -мен периодикалы өзгеріп тұрады.
-мен периодикалы өзгеріп тұрады.
Көзбен сыйымдылықтың арасында энергияның тербеленуі өтеді, ал сыйымдылыққа түсетін активтік қуат нөлге тең. Сыйымдылық кедергіні былай табуға болады: 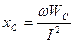 (2.30)
(2.30)
2.6R,L және C элементердің тізбектеп қосылуы
Тізбектеп қосылған R,L және C элементерден құралған электр тізбектен 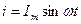 синусойдалды тоқ өткенде (2.7-сурет)
синусойдалды тоқ өткенде (2.7-сурет)
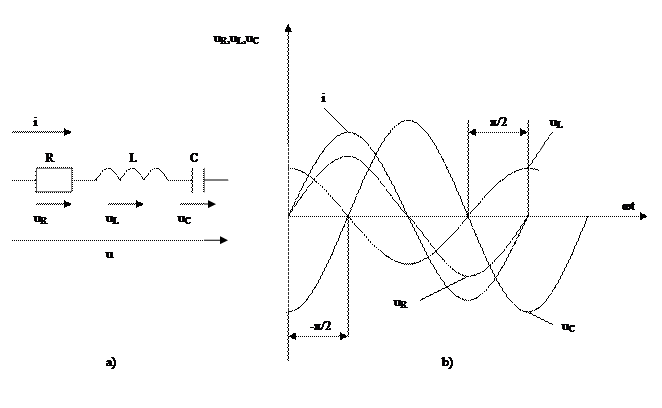

2.7-сурет. Тізбектеп қосылған кедергіде, индуктивтікте және
сыйымдылықта синусойдалы тоқ кездегі кернеулер.
бұл тізбектің шықпаларында бөлек элементтердегі синусойдалды кернеулердің қосындысына тең синусойдалы кернеу қурылады [Кирхгофтың екінші заңы]:
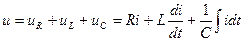 (2.31)
(2.31)
Тізбектің шықпасындағы 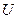 кернеу тең:
кернеу тең:
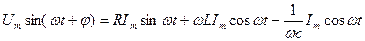
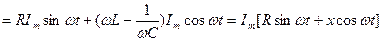 (2.32)
(2.32)
(2.32) теңдеу лезді кернеулер үшін Кирхгофтың екінші заңының жазылуының тригонометриялық түрі. Бұған кіретін шама 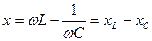 -тізбектің реактивтік кедергісі деп аталады. Бұл кедергі таңбаға қарай
-тізбектің реактивтік кедергісі деп аталады. Бұл кедергі таңбаға қарай 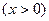 болса индуктивтік, ал
болса индуктивтік, ал 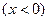 болса сыйымдылық түрлі болады.
болса сыйымдылық түрлі болады.
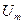 және
және 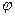 табу үшін келесі тригонометриялық қатынастарды пайдаланамыз:
табу үшін келесі тригонометриялық қатынастарды пайдаланамыз:
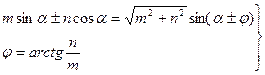 (2.33)
(2.33)
Сонымен,
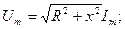
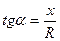 (2.34)
(2.34)
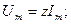
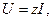 мұнда
мұнда  -тізбектің толық кедергісі.
-тізбектің толық кедергісі.
Тізбектеп 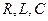 қосылған тізбектің шықпаларындағы кернеу
қосылған тізбектің шықпаларындағы кернеу 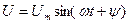 белгілі болса, онда тізбектен ағып тұрған тоқ:
белгілі болса, онда тізбектен ағып тұрған тоқ:
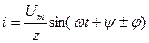 (2.35)
(2.35)
Тізбектің түрі индуктивтік болса бұрыш 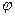 болымды
болымды 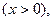 ал сыйымдылық болса-теріс
ал сыйымдылық болса-теріс 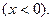
Тізбектің активтік және реактивтік кедергілердің толық кедергімен байланысы:
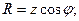
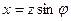 (2.36)
(2.36)
Кернеудің активтік және реактивтік құрастырушылары:
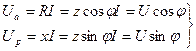
Тізбектің толық кернеуі:
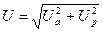 (2.37)
(2.37)
2.7R,L және C элементтердің параллельді қосылуы
Егер де 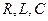 элементтер параллельді қосылған тізбекке (2.8-сурет) синусойдалды кернеу
элементтер параллельді қосылған тізбекке (2.8-сурет) синусойдалды кернеу 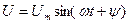 ынта салынса, онда бұл тізбектен өткен тоқ параллельді тармақтардан өтетеін тоқтардың алгебралық қосындысына тең [Кирхгофтың бірінші заңы]:
ынта салынса, онда бұл тізбектен өткен тоқ параллельді тармақтардан өтетеін тоқтардың алгебралық қосындысына тең [Кирхгофтың бірінші заңы]:
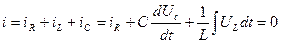 (2.38)
(2.38)


2.8-сурет. Синусойдалы кернеу кезде параллельді қосылған кедергіде, индуктивтікте және сыйымдылықтағы тоқтар.
 кедергідегі
кедергідегі  тоқ
тоқ 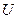 кернеумен фаза бойынша біртектес,
кернеумен фаза бойынша біртектес, 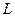 индуктивтіктегі
индуктивтіктегі 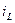 тоқ
тоқ 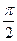 бұрышқа қалады, ал
бұрышқа қалады, ал 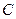 сыйымдылықтағы
сыйымдылықтағы 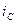 тоқ
тоқ 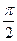 бұрышқа
бұрышқа 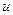 кернеуден озады (2.8-сурет).
кернеуден озады (2.8-сурет).
Тізбектегі қосындысы (жалпы) тоқ тең:
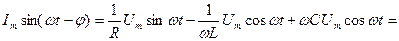
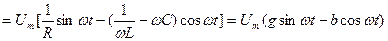 (2.39)
(2.39)
(2.39) теңдеу лездік тоқтар үшін Кирхгофтың бірінші заңының жазылуының тригонометриялық түрі. Бұған кіретін шама 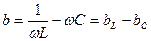 -тізбектің реактивтік өткізгіштігі деп аталады. Бұл өткізгіштік таңбаға қарай
-тізбектің реактивтік өткізгіштігі деп аталады. Бұл өткізгіштік таңбаға қарай 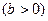 индуктивтік, ал
индуктивтік, ал 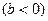 сыйымдылық түрлі болады.
сыйымдылық түрлі болады.
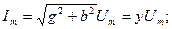
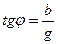 (2.40)
(2.40)
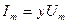 немесе
немесе 
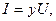 мұнда
мұнда 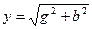 -тізбектің толық өткізгіштігі.
-тізбектің толық өткізгіштігі.
Тоқ 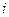 кернеу
кернеу 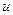 -дан бұрыш
-дан бұрыш 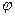 -ға не қалады, не озады.
-ға не қалады, не озады.
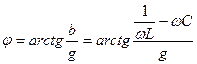
Егер де тізбектің шықпаларында кернеу 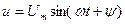 берілген болса, онда тізбектегі тоқ тең:
берілген болса, онда тізбектегі тоқ тең:
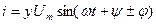 (2.41)
(2.41)
Тізбектің түрі индуктивтік болса бұрыш 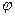 болымды
болымды 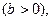 ал сыйымдылық болса теріс
ал сыйымдылық болса теріс 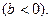
Тізбектің активтік және реактивтік өткізгіштіктердің толық өткізгішпен байланысы:
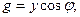
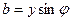 (2.42)
(2.42)
Тоқтың активтік және реактивтік құрастырушылары:
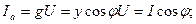
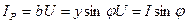 (2.43)
(2.43)
Тізбектің толық тоғы: 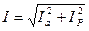
2.8Синусоидалды тоқ тізбектегі қуат
Тізбектің кернеуі 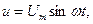 ал тоғы
ал тоғы 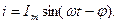
Лезді қуат:
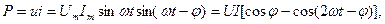 (2.44)
(2.44)
яғни екі бөліктен құралады: тұрақты шама 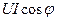 және кернеумен тоқтың жиіліктерінен екі есе үлкен синусойдалды шамадан.
және кернеумен тоқтың жиіліктерінен екі есе үлкен синусойдалды шамадан.
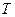 уақыт ішінде екінші қосындының орташа мәні нөлге тең. Сондықтан тізбектегі активтік қуат:
уақыт ішінде екінші қосындының орташа мәні нөлге тең. Сондықтан тізбектегі активтік қуат:
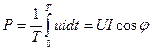 (2.45)
(2.45)
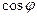 -қуат коэффициент деп аталады.
-қуат коэффициент деп аталады.
Активтік қуат басқа түрде көрсетуге болады:
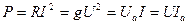 (2.46)
(2.46)
Кедергі және индуктивтігі бар тізбекті қарап шығайық. Бұл жағдайда 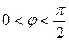 және
және 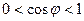 .
.
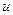 және
және 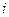 таңбалары бірдей кездегі уақыт аралықта лезді қуат болымды; энергия көзден қабылдағышқа түседі де кедергіде жұтылады және индуктивтіктің магнит өрісінде қолданады.
таңбалары бірдей кездегі уақыт аралықта лезді қуат болымды; энергия көзден қабылдағышқа түседі де кедергіде жұтылады және индуктивтіктің магнит өрісінде қолданады.
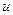 және
және 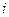 таңбалары кері кездегі уақыт аралықта лезді қуат теріс; энергияның бір бөлігі (магнит өрістегі) көзге қайтады. Активтік – сыйымдылық тізбекте көрініс ұқсас болады
таңбалары кері кездегі уақыт аралықта лезді қуат теріс; энергияның бір бөлігі (магнит өрістегі) көзге қайтады. Активтік – сыйымдылық тізбекте көрініс ұқсас болады 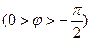 .
.


2.9-сурет. Активтік – индуктивтік тізбекке түсетін қуат.
Шінші тарау
3 Комплексті сандарды және векторлық диаграммаларды электр тізбектерді есептеуге қолдану
3.1 Синусоидалы функцияларды айнымалы векторлардың проекциялары түрінде көрсету
Электр тізбек күрделенгенде тригонометриялық түрде есептеу қиындап кетеді, ал сол себептен тұрақты тоқ тізбектерге ұқсасты айнымалы тоқ тізбектерді алгебралық түрде есептеуге рұқсат ететін әдіс керек болады. Мұндай ыңғайлы әдіс ретінде синусойдалы функцияларды құрауды айнымалы векторларды қарауға ауыстыруға орнатылған комплексті әдіс.
 |
Комплексті жазықтықта әрбір нүкте бұл нүктені радиус-векторымен белгіленеді. Вектордың басы координат басымен үйлеседі, ал аяғы берілген комплексті санға сәйкесті нүктеде жатады (3.1-сурет).
3.1-сурет. Комплексті санды бейнейлейтін вектор.
Комплексті санды көрсеткіш немесе полярлы түрде жазуға болады:
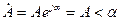 (3.1)
(3.1)
мұнда 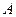 -модуль;
-модуль; 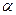 -аргумент немесе фаза;
-аргумент немесе фаза; 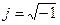
Комплексті санның тригонометриялық түрде жазылуы:
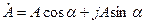 (3.2)
(3.2)
және оның алгебралық түрі:
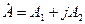 (3.3)
(3.3)
мұнда 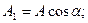
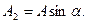
Демек,
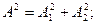
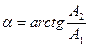 (3.4)
(3.4)
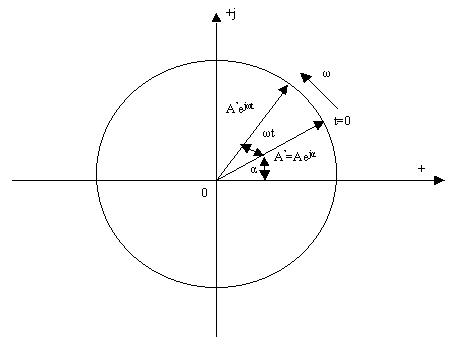
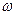 бұрыштық жылдамдықпен болымды бағытпен, яғни сағат тіліне қарсы, айналып тұрған векторды былай көрсетуге болады:
бұрыштық жылдамдықпен болымды бағытпен, яғни сағат тіліне қарсы, айналып тұрған векторды былай көрсетуге болады:
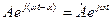 (3.5)
(3.5)
мұнда 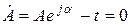 уақыт мезгілде векторды көрсететін комплекстіамплитуда (3.2-сурет). Басқаша айтқанда, бұл уақыттан тәуелсіз, модуль және аргументы берілген синусоидалды функцияның амплитудасына және басты фазасына тең комплексті шама.
уақыт мезгілде векторды көрсететін комплекстіамплитуда (3.2-сурет). Басқаша айтқанда, бұл уақыттан тәуелсіз, модуль және аргументы берілген синусоидалды функцияның амплитудасына және басты фазасына тең комплексті шама.
 |
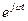 көбейткіш – айналдыру оператор. Комплексті амплитуда
көбейткіш – айналдыру оператор. Комплексті амплитуда 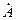 -ны
-ны 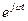 көбейту болымды бағытқа вектор
көбейту болымды бағытқа вектор 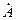 -ны бұрыш
-ны бұрыш 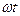 бұруды көрсетеді.
бұруды көрсетеді. 3.2-сурет. Айналмалы вектор.
(3.5) функцияны тригонометриялық түрде жазғанда шығады:
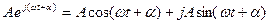
Қорытқанда, 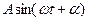 синусоидалды функция
синусоидалды функция 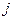 көбейткішсіз алынған комплексті (3.5) функцияның жорымал бөлігі немесе айналмалы вектордың жорамалды білікке проекциясы.
көбейткішсіз алынған комплексті (3.5) функцияның жорымал бөлігі немесе айналмалы вектордың жорамалды білікке проекциясы.
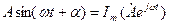 (3.6)
(3.6)
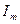 -комплексті функцияның жорамал бөлігі алынғанын көрсетеді.
-комплексті функцияның жорамал бөлігі алынғанын көрсетеді.
Егер де синусоидалды функциялардың жиіліктері бірдей болса, онда бұл функцияларға сәйкесті векторлар бірдей бұрыштық жылдамдықпен айналады, ал сол себептен олардың арасындағы бұрыштар өзгермейтін болып сақталады.
3.3,а-суретте бұрыштық жиіліктері 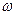 бірдей екі синусойдалды функциялар
бірдей екі синусойдалды функциялар 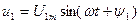 және
және 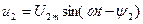 көрсетілген. Функция
көрсетілген. Функция 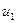 фаза бойынша функция
фаза бойынша функция 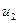 -деп озып тұр, фазалық ығысу басты фазалардың айырымына тең:
-деп озып тұр, фазалық ығысу басты фазалардың айырымына тең:
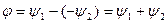
3.3,b-суретте бұл бұрышты өздері ара векторлар құрып тұр.
Басты фазалар тең кезде, яғни фазалық ығысу нөлге тең болғанда, векторлар бір жаққа бағытталады (фаза бойынша біртектес).
Фазалық ығысу 180° болғанда векторлар қарама-қарсы жақтарға бағытталады (қайшы фазада болады).
Фаза бойынша олардың өзара бағытта болуды сақтаумен құрылған векторлардың жиынтықтарын бейнелейтін диаграмма векторлық диаграмма деп аталады.
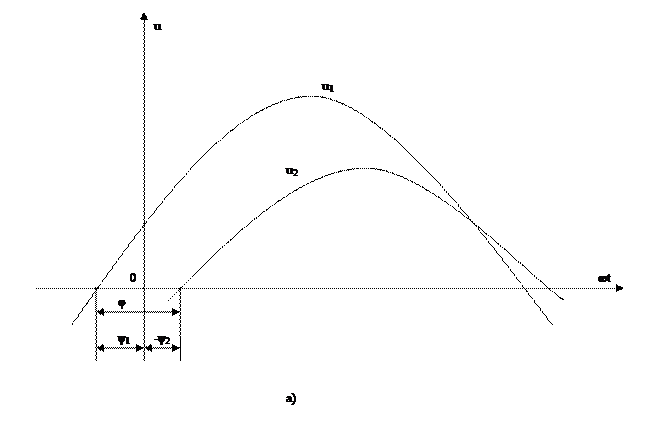

3.3-сурет
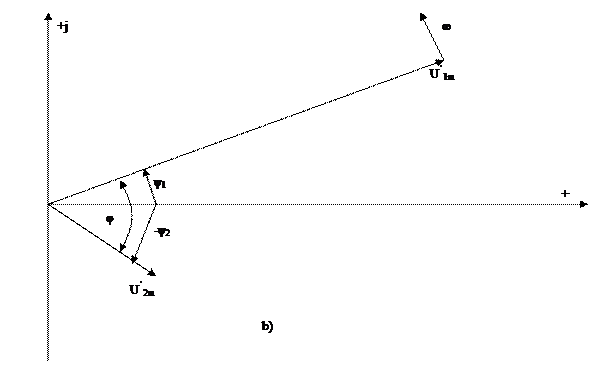

3.3-сурет
3.2 Комплекстік түрдегі Ом және Кирхгофтың заңдары
а) 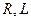 және
және 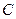 -нің тізбектеп қосылуы
-нің тізбектеп қосылуы
Кирхгофтың екінші заңы бойынша жазылған теңдеуде
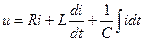 (3.7)
(3.7)
