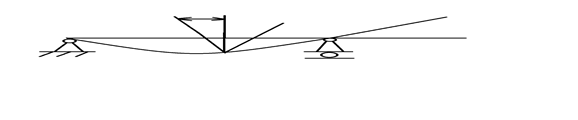
Построим эпюры нормальных и касательных напряжений для выбранного сечения.

Эпюры s и τ для двутаврового сечения, профиль которого работает на изгиб, имеют конкретный вид и представлены на рисунке 4. Необходимо определить и расставить значения нормальных и касательных напряжений в характерных точках сечения:

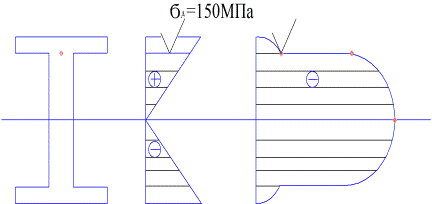
рис. 4

1.Точка на поверхности сечения.

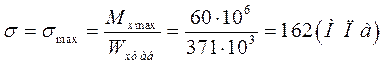
τ = 0 (МПа)

2.Точка А в сечении.

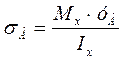, это значение было рассчитано нами ранее и составляет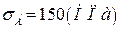

В отличие от нормального напряжения, касательное в точке А сечения будет иметь два значения, т.к. только в этом месте двутавр имеет две ширины, b=6(мм)-ширина ножки, В=125(мм)-ширина полочки. Обозначим эти напряжения как τ_А и τٰ_А.

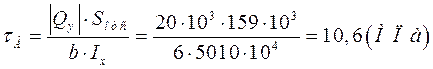
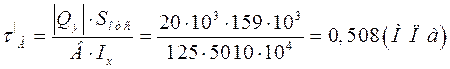
3.Центр сечения (Нейтральная линия).

s = 0 (МПа);

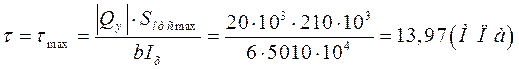
2-ая часть. Определение перемещений (прогибов и углов поворота) в балке методом начальных параметров.

Пояснение: Для выполнения данной части контрольной работы в методическом указании представлен пример, в котором рассматриваемая балка двутаврового поперечно сечения нагружена внешними силовыми факторами, отличающимися по значениям и месту приложения, по сравнению с первой частью. Это сделано для более подробного пояснения по решению второй части, чтобы рассмотреть все возможные вопросы, которых могло бы не быть при иной схеме задания. Однако для студента в контрольной работе обе части являются одной целой задачей и значения, полученные в первой половине, являются фундаментом для решения второй.

Для заданной балки определить методом начальных параметров угол поворота и прогиб по середине пролёта. По эпюре изгибающего момента М_x построить форму изогнутой оси балки.

Сославшись на вышесказанное пояснение, помимо исходных данных q, M и F, после решения первой части будем иметь эпюры В.С.Ф.(см. рис.5), а так же следующие необходимые нам данные (подчеркнуто):

q = 10(кH/м), M = 20(кH*м), F=50(кН), R_A = 35(кH), R_B = -65(кH), № двутавра 33, W_x = 597*10³ (мм³), I_x = 9840*10⁴(мм⁴)

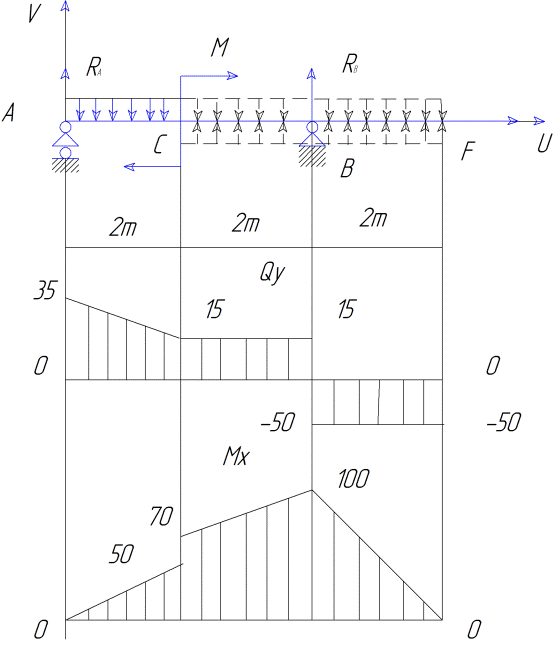
рис. 5

Для определения перемещений балки запишем обобщённое уравнение изогнутой оси.

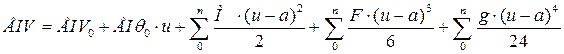(2.1.)

где а- расстояние от начала геометрической системы координат до места приложения силы, момента или начала распределенной нагрузки.

РЕШЕНИЕ.

Для начала решения необходимо выполнить ряд подготовительных операций:

1). Начало геометрической системы координат (u-V) выбирают и располагают на конце балки, желательно на опоре (см. рис.5), при этом начало балки совпадает с началом координат, а конец будет противоположно.

2). Если балка загружена распределённой нагрузкой, не доходящей до её конца, то нагрузку необходимо продлить до конца балки, а чтобы не произошло ни каких изменений, приложить точно такую же с противоположной стороны (см. рис.5). В начало балки распределенную нагрузку продлевать не нужно.

1.Запишем уравнение прогибов и углов поворота для тех участков балки в которые входят опоры А и В и сечение в котором определяют перемещение т.С.

1. Участок 0≤u₁≤2 м

Уравнение прогибов на первом участке будет иметь вид:

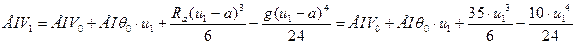(2.2.)

Для получения уравнения углов поворота на первом участке необходимо взять первую производную от уравнения (2.2.).

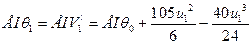(2.3.)

2. Участок 2≤u₂≤4м

Уравнение прогибов на втором участке будет иметь вид:

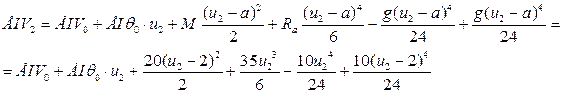(2.4.)

Для получения уравнения углов поворота на втором участке необходимо взять первую производную от уравнения (2.4.).

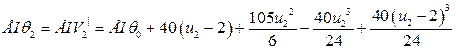(2.5.)

2.Запишем условие на опорах. Так как на опорах балки прогиб равен 0 то:

Если u₁ = 0(м), то V₁ = 0(м). (2.6.)

Если u₂ = 4(м), то V₂ = 0(м). (2.7.)

Подставим условие (2.6.) в уравнение (2.2.).

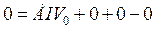, следовательно 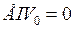. (2.8.)

Подставим условие (2.7.) и (2.8.) в уравнение (2.4.).

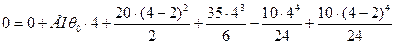
Преобразовав это уравнение, получим:

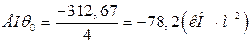(2.9.)

3.Запишем условие для точки, в которой определяем прогиб, (в нашем случае это середина пролета балки, т.е. точка С.)

Пояснение: Середина пролета балки т.С может находиться как на границе первого и второго участков так и на любом из них в отдельности!

В нашем случае можно рассматривать любой из двух участков (например, 1-ый)

Если u₁ =2м, то V₁=V_c (2.10)

Подставим условия (2.8.) (2.9.) (2.10.) в уравнение (2.2.).

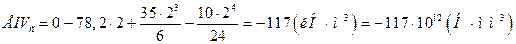
Подставим в полученное выражение значения модуля нормальной упругости Е=2*10⁵ (МПа), момента инерции I_x=9840*10⁴ (мм⁴) и выразим прогиб:

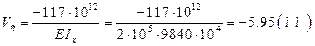
Так прогиб получился отрицательный то сечение С перемещается в сторону противоположную от направления оси V т.е. вниз.

Сравним полученный прогиб балки 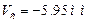с допускаемым прогибом 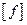который равен:

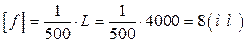, где L- длина пролета балки.

Очевидно, что условие жесткости выполняется т.к.:

,

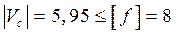Если условие жёсткости не выполняется нужно взять двутавр большего поперечного сечения, определить прогиб (при этом изменится только значение I_х) и сравнить с допускаемым.

4.Запишем условие для точки, в которой определяем угол поворота сечения, (в нашем случае это середина пролета балки, т.е. точка С.)

Если u₁ =2м, то θ₁=θ_c (2.11)

Подставим условия (2.9.) (2.11.) в уравнение (2.3.).

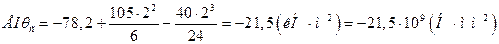
Подставим в полученное выражение значения модуля нормальной упругости Е=2*10⁵ (МПа), момента инерции I_x=9840*10⁴ (мм⁴) и выразим угол поворота:

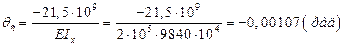
Если начало координат располагается на левом конце балки, как в нашем случае, то положительным считается поворот сечения направленный против часовой стрелки и наоборот.

Если начало координат располагается на правом конце балки, то положительным считается поворот сечения направленный по часовой стрелки и наоборот.

5.Построим изогнутую ось балки.

Изогнутая ось балки строится по эпюре изгибающего момента М_х

В том месте, где М_х >0 балка имеет вогнутый вид

В том месте, где М_х <0 балка имеет выпуклый вид

В нашем случае вся эпюра изгибающего момента находится выше нулевой линии. Изображаем вогнутую балку (см. рис.6).