Статистические методы выявления наличия корреляционной связи между признаками.

СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ

Статистические методы выявления наличия корреляционной связи между признаками.

Уравнение регрессии и значение его расчета (однофакторный анализ, многофакторный анализ).

Измерение степени тесноты корреляционной связи между признаками.

Статистические методы выявления наличия корреляционной связи между признаками.

Связи между признаками и явлениями, ввиду их большого разнообразия, классифицируются по ряду оснований. Признаки по их значению для изучения взаимосвязи делятся на два класса. Признаки, обусловливающие изменение других, связанных с ними признаков, называют факторными. Признаки, изменяющиеся под действием факторных признаков, называют результативными. Связи между явлениями и их признаками классифицируются по степени тесноты, по направлению и по аналитическому выражению.

В статистике различают функциональную связь и стохастическуюзависимость.

Функциональные связи характеризуются полным соответствием между причиной (факторный признак) и следствием (результативный признак), каждому факторному признаку соответствует одно или несколько вполне определенных значений результативного признака.

При стохастической связи каждому отдельному значению факторного признака х отвечает определенное множество значений результативного признака у. Такая связь образует условное распределение признаков, которое варьируется. Связи такого рода называют стохастическими, вероятностными. Частным случаем стохастической связи является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков.

Чаще всего, закономерности массовых общественных явлений складываются под влиянием множества причин, которые действуют одновременно и во взаимной связи, причем точно неизвестно, в какой мере каждая из них влияет на величину явлений. В корреляционных связях между причиной и следствием нет полного соответствия, а наблюдается лишь известное соотношение. Каждому значению факторного признака соответствует при этом ряд значений результативного признака, не имеющих строго определенной величины. Причем с изменением факторного признака меняется средняя величина результативного признака. Например, между заработной платой рабочих и их производственным стажем имеется связь - обычно, чем выше стаж, тем выше заработная плата. Но эту связь нельзя вывести математической формулой, т.к. на зарплату будут еще влиять – квалификация, состояние оборудования и т.д., влияние которых может привести к снижению зарплаты.

По направлению выделяют связь прямую и обратную.

По аналитическому выражению выделяют связи прямолинейные (линейные) и нелинейные (криволинейные).

В статистическом анализе общественных явлений и процессов применяется ряд методов, которые дают представление о наличии и характере взаимосвязи.

1. Метод сравнения параллельных рядов.

2. Метод аналитических группировок.

3. Балансовый метод.

4. Корреляционный метод.

Корреляционный анализ применяется в экономических исследованиях после предварительного качественного анализа изучаемого явления, когда устанавливается наличие связи между явлениями и характер этой связи.

Корреляционный анализ общественных явлений проходит через три этапа.

1-ый этап заключается в математико-экономическом моделировании, т.е. в построении корреляционного уравнения, которое выражает характер связи между изучаемыми явлениями или признаками.

,

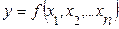где y- результативный признак;

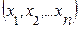- факторные признаки.

2-й этап представляет собой решение принятой модели путем нахождения параметров корреляционного уравнения.

3-й этап- оценка и анализ полученных результатов.

От правильности выбора корреляционной модели (уравнения) зависит конечный результат всего статистического исследования взаимосвязи между рассматриваемыми признаками. Если корреляционная модель определена неверно, то какие бы не применялись методы ее решения и оценки характер связи между изучаемыми признаками получить не удастся.