Основные источники погрешностей и методы их компенсации
В состав специальных угло-измерительных устройств, используемых для настройки и проверки узлов беспилотных летательных аппаратов, часто входят резистивные преобразователи угла. Эти преобразователи требуют проверки их основных характеристик и в частности значения коэффициента преобразования и нелинейности функции преобразования. Указанные характеристики определяют по результатам измерения функциональной зависимости между углом поворота оси преобразователя и электрической величиной, например, сопротивлением или напряжением. Для измерения электрических величин существует большая номенклатура измерительных приборов, имеющих высокую точность, тогда как для измерения угла поворота оси преобразователя можно использовать довольно ограниченное число угло-измерительных приборов. Для измерения угла поворота оси преобразователя можно использовать прямой метод измерения с использованием угломерных шкал [1]. Этот метод реализуется с помощью гониометров и оптических делительных головок, имеющих угломерные шкалы. Принцип работы гониометров основан на свойстве авто-коллимации. Осуществление этого принципа требует наличия плоской зеркальной поверхности, расположенной перпендикулярно оси автоколлиматора гониометра и жёстко связанной с осью преобразователя. Для этого необходимо изготовить деталь с высокими требованиями к плоскостности и чистоте зеркальной поверхности, решить конструктивную задачу по креплению этой детали на оси преобразователя, закрепить преобразователь на столике гониометра и провести юстировку относительно оси автоколлиматора. Решение всех этих задач требует значительных материальных и временных затрат. Использование оптических делительных головок также не возможно без разработки и изготовления крепёжных приспособлений и переходных муфт, которые вносят дополнительные погрешности при измерении углов и требуют отдельного исследования своих метрологических характеристик. Таким образом, исходя из анализа методов и измерительных устройств, которые можно использовать для измерения углов поворота оси преобразователя, была сформулирована задача: необходимо разработать простой метод измерения углов поворота оси преобразователя, не требующий разработки и изготовления сложных крепёжно-установочных приспособлений и переходных муфт. Алгоритм координатного метода измерения углов поворота оси преобразователя Поставленная задача была решена но основе координатного метода с использованием в качестве измерителя координат универсального измерительного микроскопа УИМ-23. Определение преобразовательной характеристики преобразователей угла связано с многократным измерением углового положения оси преобразователя в пределах всего диапазона поворота оси. Для этого определяют координаты точки, Метрология жёстко связанной с осью и расположенной на расстоянии R от оси вращения. Практическая реализации этого условия осуществлялась путём закрепления на оси преобразователя рычага, располагаемого перпендикулярно оси вращения преобразователя, выборе или нанесении на рычаге метка, которая использовалась в качестве вращающейся точки. Вращая ось из одного крайнего положения в другое, определялись координаты выбранной метки в фиксированных угловых положениях оси. Учитывая, что диапазон вращения оси измерительных преобразователей, как правило, меньше 360°, первичный центр, выбранный каким-либо методом (например, как центр окружности, проходящей через три точки), нельзя принимать за базовый, относительно которого определяются углы поворота. При этом найти центр вращения на основе оптимизации погрешностей углов, как в случае секторных шкал [2-4] не представляется возможным по причине отсутствия номинального (действительного) значения углов, с которыми сравнивают измеренные углы. Поэтому центр вращения было предложено выбирать на основании оптимизации функции распределения отклонений траектории точки вращения от радиуса окружности, принятой за базовую. При этом радиус базовой окружности выбирают равным среднему значению радиуса траектории. Алгоритм метода определения угла поворота оси преобразователя угла состоит в следующем.
1. Определяют координаты фиксированных положений вращающейся точки Qi (xi,yi).
2. Определяют координаты предварительного (первичного) центра вращения О1(xо1,yо1).
3.Определяют расстояния Ri от первичного центра вращения до фиксированных положений вращающейся точки.
4.Определяют среднее расстояние Rср от первичного центра вращения до фиксированных положений вращающейся точки.
5. Определяют отклонения ΔRi расстояний от первичного центра вращения до фиксированных положений вращающейся точки.
6. Выбирают критерий оптимизации функции распределения отклонений расстояний ΔRi и вычисляют его значение (характеристики в случае геометрического критерия).
7.Минимизируют (оптимизируют) значение критерия путём последовательного изменения координат центра вращения.
8. Центр вращения, координаты которого получены в результате оптимизации функции распределения отклонений расстояний ΔRi, принимают в качестве оптимального.
9. Вычисляют угловые значения фиксированных положений вращающейся точки.
На рисунке 1 в качестве иллюстрации приведены функции распределения отклонений расстояний фиксированных положений вращающейся точки от радиуса базовой окружности до проведения оптимизации (график 1), при этом центр окружности определялся по трём точкам, и после оптимизации (график 2).
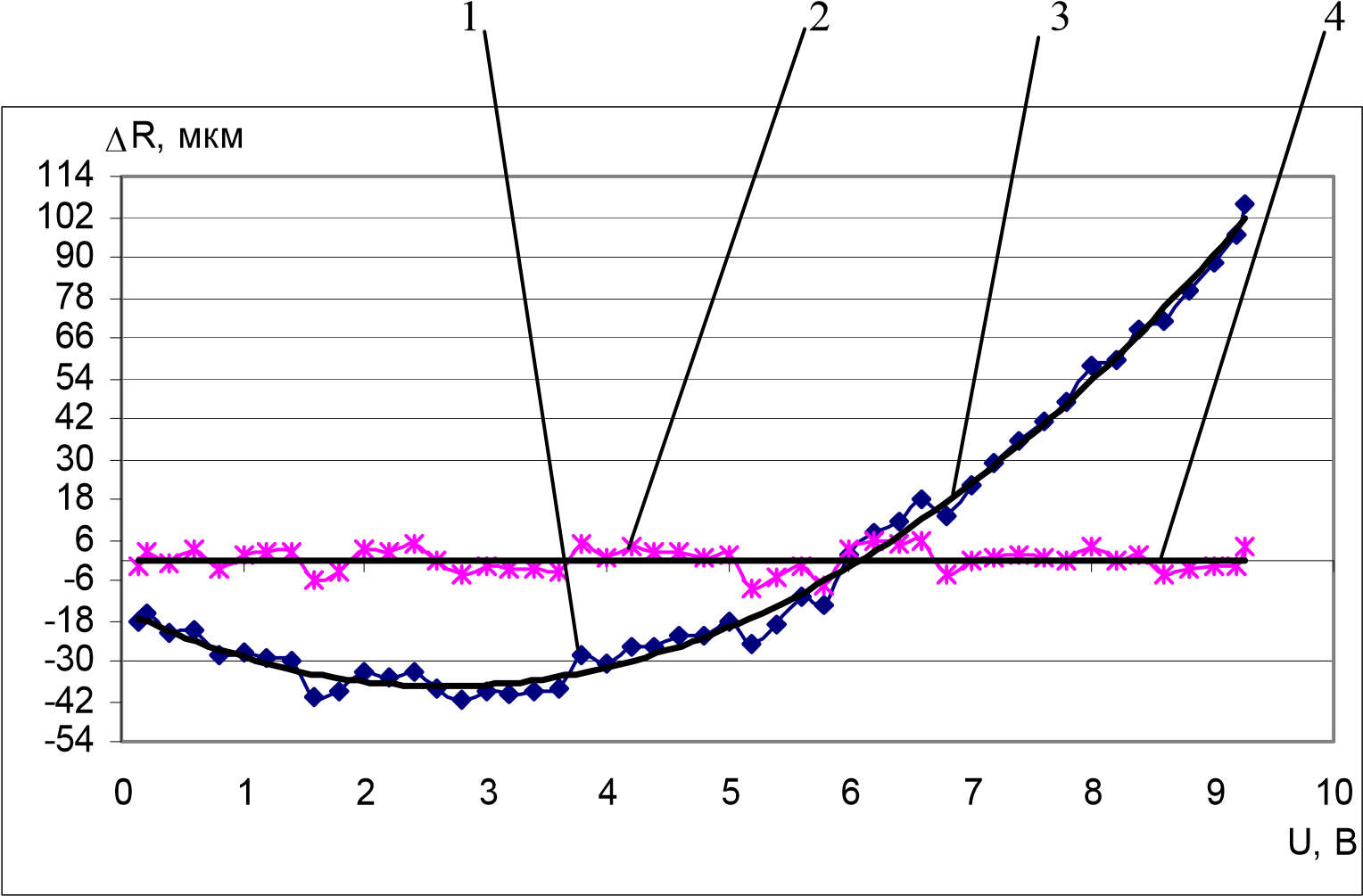
Рисунок 1.
Результаты вычислений получены при исследовании преобразователя с диапазоном углов поворота 45°. В качестве критерия оптимизации выбрана аппроксимирующая парабола, которая путём изменения координат центра вращения приводится к прямой, параллельной оси Х. На рисунке 1 также приведены аппроксимирующие параболы функций распределения радиусов до (график 3) и после (график 4) оптимизации. Предложенный метод имеет высокую чувствительность по смещению центра базовой окружности, поскольку смещение базового центра вращения от первичного составляет всего 0,89 мм, а наклон аппроксимирующих парабол имеет значительное различие как Метрология визуальное (рисунок 1), так и числовое: коэффициенты уравнений парабол, характеризующие наклон, отличаются в 346 раз. Изменение угловых значений фиксированных положений вращающейся точки при переходе от первичного центра к оптимальному показано на рисунке 2. Процесс оптимизации функции распределения отклонений расстояний ΔRi приводит к уменьшению систематической погрешности, значение которой описывается аппроксимирующими параболами рисунка 1. Надо отметить также, что размах значений функции распределения радиусов (рисунок 1, график 2), равный 14 мкм, характеризует поперечный люфт оси преобразователя углов. 1 2 3 4 -54 -42 -30 -18 -6 6 18 30 42 54 66 78 90 102 114 0 1 2 3 4 5 6 7 8 9 10 U, В ΔR, мкм
1 ─ функция распределения до оптимизации,
2 ─ функция распределения после оптимизации,
3 ─ аппроксимирующая парабола функции распределения отклонений расстояний до оптимизации,
4 ─ аппроксимирующая парабола функции распределения отклонений радиусов после оптимизации. Рис. 1. Функции распределения отклонений расстояний ΔRi фиксированных положений вращающейся точки от среднего радиуса 0 100 200 300 400 500 600 700 800 900 1000 1100 0 2 4 6 8 10 U, B Δα, сек
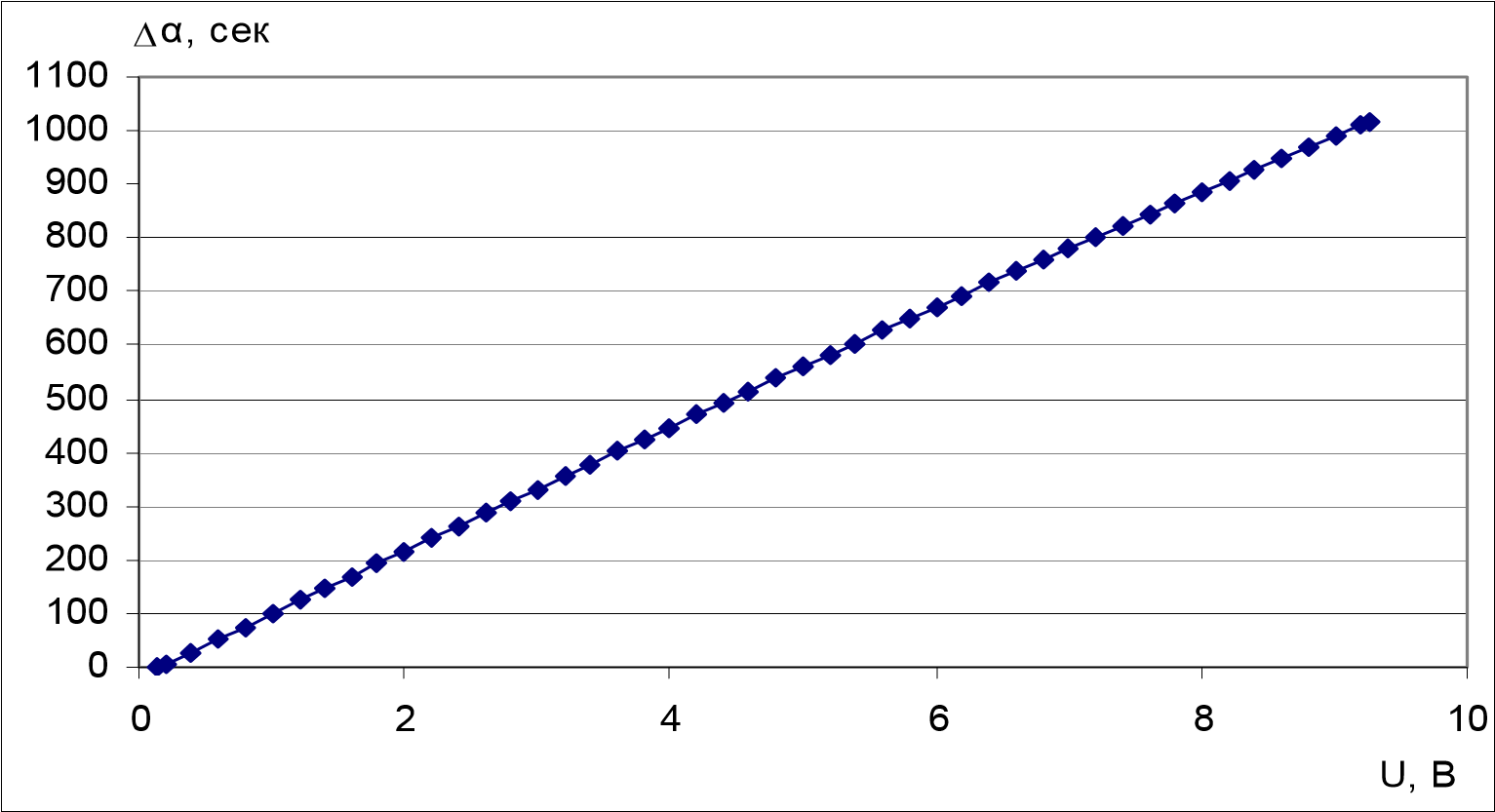
Рисунок 2. Изменение угловых значений фиксированных положений вращающейся точки после оптимизации
После оптимизации и определения метрологического центра вращения, вычисляют угловые значения фиксированных положений вращающейся точки относительно оптимального центра по формулам, взятым из [5].
Уравнение прямой, проходящей через две точки Р1(x1,y1), Р2(x2,y2) y = k ⋅ x + b,
Угол между двумя прямыми с угловыми коэффициентами k1 и k2 определяется k2 − k1 по формуле α= arctg
1+ k2 ×k1
На основании полученных значений углов строят преобразовательную функцию преобразователя U = f (α), по которой определяют коэффициент преобразования и нелинейность функции преобразования.
Выводы
1. В работе предложен новый простой координатный метод определения углов поворота оси резистивного преобразователя углов, не требующий разработки и изготовления сложных крепёжно-установочных приспособлений и переходных муфт.
2. Особенностью предложенного метода является нахождение оптимального центра вращения при оптимизации по выбранному критерию функции распределения отклонений траектории вращающейся метки от базовой окружности.
3. Результаты расчёта по предложенному способу позволяют также оценить значение радиального люфта оси преобразователя.
Статические характеристики описывают свойства преобразователя при работе в лабораторных условиях с малыми изменениями измеряемой величины. Эти характеристики называются градуировочными. Условия измерений - температура 25°С, влажность < 90%, нормальной давление 100 кПа.
Основной характеристикой ИП является функция преобразования Y=f(X), определяющая зависимость выходной величины Y от входной X, которые представляют собой истинные (при теоретическом анализе) и действительные (при экспериментальных исследованиях) значения величин. Чаще всего эта зависимость описывается аналитическим выражением, иногда графически или задается в виде таблицы. В качестве обобщенной характеристики ИП данного типа принимается некоторая усредненная функция преобразования большой группы однотипных преобразователей.
Отношение выходной величины Y ко входной Х называется коэффициентом преобразования k(X)= Y/X - в общем случае - функция входной преобразуемой величины.
Производная от функции преобразования S=dY/dX=F’(X) называется чувствительностью ИП. Чувствительность характеризует степень реагирования ИП на входную величину. Для преобразователей функция преобразования которых линейна, чувствительность будет постоянной. Если же функция преобразования не линейна, то чувствительность является функцией входной величины и связана с коэффициентом преобразования зависимостью
Для характеристики нелинейных ИП используют понятие средней чувствительности в диапазоне преобразований
Yê −Yí (2)
Sñð = ,
Xê − Xí
где Yк- Yн и Xк - Xн - диапазоны преобразований соответственно по выходной и входной величинам; Yк, Yн , Xк , Xн - конечныйи начальный пределы преобразований.
Под относительной чувствительностью ИП понимают отношение относительного изменения выходной величины к относительному изменению входной:
Следует отметить, что изменение выходного сигнала ИП может быть обусловлено также влиянием неинформативного параметра входного сигнала. Поэтому говорят о чувствительности ИП к неинформативным параметрам. В общем случае полное приращение выходного сигнала с учетом влияющих неинформативных параметров
неинформативным параметрам a, b, ..., m, ..
Номинальными характеристиками называют действительные, полученные в результате эксперимента. Они учитывают все параметры (факторы), влияющие на результат эксперимента.
Диапазон измерений - область значений измеряемой величины, в пределах которой нормированы погрешности средства измерений.
Точность измерений - характеризует близость измеренного значения физической величины к действительному. Количественное выражение точности - погрешность. Погрешности могут быть классифицированы по различным признакам: способу выражения (абсолютные, относительные и приведенные), условиям возникновения (основные и дополнительные), степени неопределенности (систематические и случайные) и др.
Наибольшая точность, с которой осуществляются измерения - разрешающая способность. Обобщенная характеристика, определяющая пределы допустимых погрешностей - класс точности.
