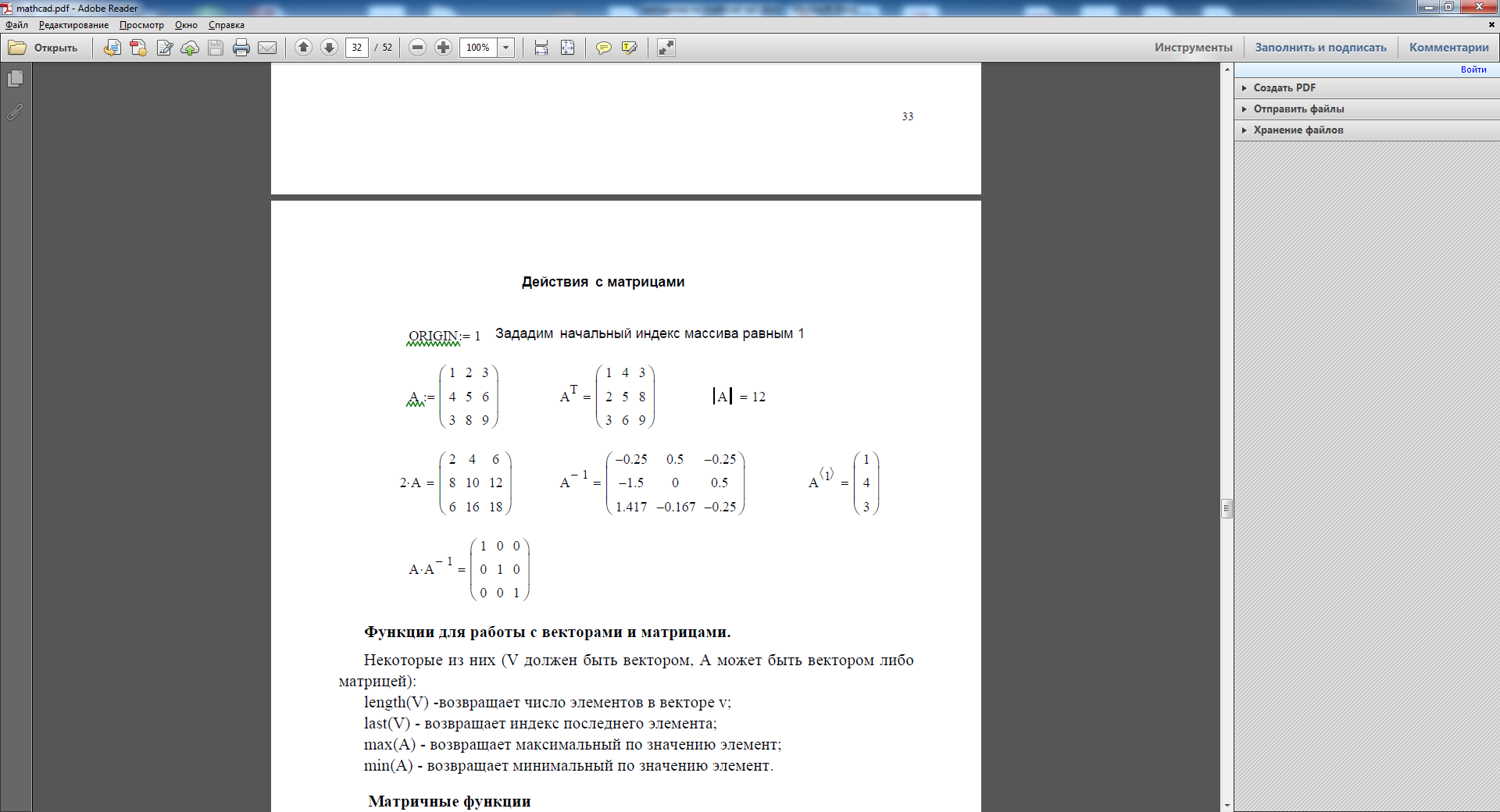
Операторы для работы с массивами

Обозначения: для векторов - V, для матриц - М и для скалярных величин - z.

3.5 Задания к лабораторной работе 2

1. Ввести в документ название лабораторной работы, вариант задания и фамилию студента

2. Создать квадратные матрицы А, В, D, размером (5,5,4 соответственно) первым способом

3. Исследовать следующие свойства матриц на примере преобразования заданных массивов:

• транспонированная матрица суммы двух матриц равна сумме транспонированных матриц (A+B)^T=A^T+B^T ;

• транспонированная матрица произведения двух матриц равна произведению транспонированных матриц, взятых в обратном порядке: (A*B)^T=B^T*A^T ;

• при транспонировании квадратной матрицы определитель не меняется : |D|=|D^T|;

• произведение квадратной матрицы на соответствующую ей квадратную дает единичную матрицу (элементы главной диагонали единичной матрицы равны 1, а все остальные – 0) D*D^-1=E.

4. Для матриц A,B найти обратные матрицы.

5. Найти определители матриц A,B.

6. Для матрицы А увеличить значения элементов в № раз, где № - номер варианта.

7. Для матрицы В увеличить значения элементов на №.

8. Создать вектор C вторы м способом, количество элементов которого равно 6.

9. Применить к матрицам А, В, D две-три встроенные матричные функции из диалога

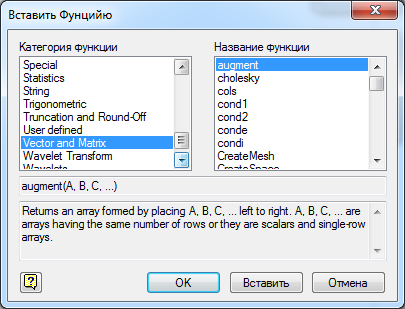
10. Применить к вектору С две-три встроенные векторные функции инструмента «Вставить функцию».

11. Сохранить документ.

Контрольные вопросы

1. Как создать матрицу, вектор - строку, вектор - столбец?

2. Какие операторы есть для работы с матрицами?

3. Перечислите команды панели инструментов Матрицы.

4. Как вставить матричные функции?

5. Как выполнять вычисления, если матрица задана в символьном виде?

Лабораторная работа 3.

Решение уравнений и символьные вычисления в MathCAD

4.1. Цель работы

Научиться решать уравнения и выполнять символьные преобразования в среде математических расчетов MathCAD.

4.2. Постановка задачи

Выполнить символьные преобразования согласно варианта и построить графики функций.

4.3. Внеаудиторная подготовка

Для подготовки к лабораторной работе следует ознакомиться с [9] (С.В.Глушаков. Математическое моделирование. Mathcad 2000. Учебный курс / Харьков: Фолио, 2001. - 524 с.).

4.4. Краткие теоретические сведения

Огромное количество задач вычислительной математики связано с решением нелинейных алгебраических уравнений, а также систем таких уравнений. При этом необходимость решения нелинейных уравнений возникает зачастую на промежуточных шагах, при реализации фрагментов

более сложных алгоритмов (к примеру, при расчетах дифференциальных уравнений при помощи разностных схем и т. п.).