Збільшимо число комірок в п'ять разів.

МЕТОДИЧНІ ВКАЗІВКИ

та вихідні дані до розрахунково-проектувальної роботи №2

"Розрахунок балок-стінок методом скінчених різниць"

з курсу "Чисельні методи розрахунку просторових конструкцій"

Одеса-2017

ЗМІСТ стор.

ЗАГАЛЬНІ ВКАЗІВКИ ……………………………………………………..
РПР №2. РОЗРАХУНОК БАЛКИ-СТІНКИ МЕТОДОМ СКІНЧЕНИХ РІЗНИЦЬ..………………………………………………………………………
1.1.	Склад завдання ………………………………………………………..
1.2.	Методичні вказівки .………………………………………………….
1.3.	Приклад розрахунку балки-стінки …………………………………..
1.4.	Стислий опис програми " ВИСОКА-БАЛКА" ……………………..
1.5.	Приклад розрахунку балки-стінки за допомогою ПК ……………..
1.6.	Контрольні запитання ………………………………………………..
1.7.	Вихідні дані до РПР, додаток № 1 …………………………………..
	Література ……………………………………………………………..

ЗАГАЛЬНІ ВКАЗІВКИ

Розрахунково-проектувальна робота (РПР-2) виконується на аркушах креслярського паперу формату А2 (594х420 мм) з прикладенням пояснювальної записки, відповідно шифру, вказаного викладачем (трицифрове число).

На креслення повинні бути винесені: задана схема з вказівкою розмірів і навантажень, таблиці або епюри внутрішніх зусиль (напружень) та переміщень, умовні позначення.

Пояснювальна записка повинна мати вихідні дані, робочі формули, пояснення до них, розрахунки, таблиці, проміжні результати і т.д.

Перед виконанням РПР студент зобов’язаний ознайомитися з відповідними розділами рекомендованої літератури, розібрати приклади, відповісти на контрольні запитання.

І. РПР №2. РОЗРАХУНОК БАЛКИ-СТІНКИ ЗА МЕТОДОМ СКІНЧЕНИХ РІЗНИЦЬ.

1.1 Склад завдання.

- Заномерувати вузли сітки згідно з додатком №1, прийняти замінюючи раму.

- Визначити згинальні моменти та поздовжні сили для стержнів замінюючої рами, побудувати епюри M і N.

- Скласти систему скінчено-різницевих рівнянь та розв’язати її. Обчислити величини напружень.

- Побудувати епюри напружень в перерізах для сітки 5х3 комірок.

- Зробити статичні та деформаційну перевірки.

- Підготувати вихідні дані для розрахунку за програмою "ВИСОКА-БАЛКА" та здати їх викладачеві для перевірки.

- Отримати результати за допомогою програми "ВИСОКА-БАЛКА" зі збільшеним числом внутрішніх вузлів в 5-10 разів.

- Побудувати епюри напружень в перерізах для сітки зі збільшеною кількістю комірок.

- Порівняти отримані результати.

1.2 Методичні вказівки.

Розрахунково-проектувальна робота ставить своєю метою розрахунок прямокутних балок-стінок одиничної товщини, які не мають статично невизначних опорних закріплень, з однозв’язним контуром, тобто зводиться до розв’язку першої основної задачі теорії пружності ( у напруженнях ). Цей розрахунок полягає в відшукуванні функції напружень 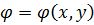, що задовольняє бігармонічне рівняння

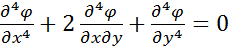(2.1)

та задані граничні умови.

Напруження визначаються через функцію напружень 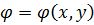згідно залежностям (при відсутності об’ємних сил):

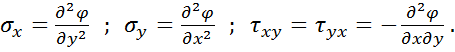(2.2)

Розв’язок рівняння (2.1) може бути здобути одним із чисельних методів – зокрема, методом скінчених різниць. Метод базується на наближеному визначенні величин, що відшукуються, у вузлах сітки, нанесеної на область. В основі, що розглядується методу лежить формула для центральної різниці першого порядку (рис.2.1):

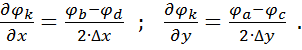(2.3)

Задана область балки-стінки при цьому апроксимується сіткою, у загальному випадку прямокутною, з розмірами комірки 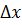і 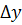. Зі збільшенням кількості комірок зростає точність методу, проте ще в більш значній мірі зростають витрати часу, що потребує застосування персонального комп’ютера.

Шляхом заміни похідних у рівнянні (2.1) різницевими відношеннями дістанемо систему лінійних алгебраїчних ІЗ-членних різницевих рівнянь, кожне з яких записано для одного з внутрішніх вузлів сітки. Для точки "К" (рис.2.1) скінчено-різницеве рівняння має вигляд:

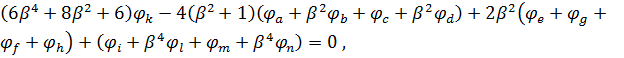(2.4)

де

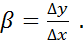(2.5)

Для квадратної сітки 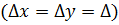рівняння (2.4) спрощується:

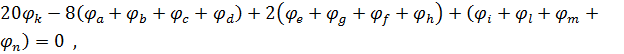(2.6)

Алгебраїчні рівняння (2.4) або (2.6), записані для двох внутрішніх прилеглих до контуру рядів точок, будуть мати, окрім невідомих значень φ=φ(x,y) у внутрішніх вузлах, також відомі значення функції напружень в контурних та поза контурних точках.

Для визначення функції напружень в контурних та позаконтурних вузлах використовується рамна аналогія. У розрахунок приймається замінюючи рама, яка своїми обрисами та розмірами відповідає контурові балки-стінки; окрім того, рама навантажена тими ж силами, що й балка-стінка, та має ті ж закріплення.

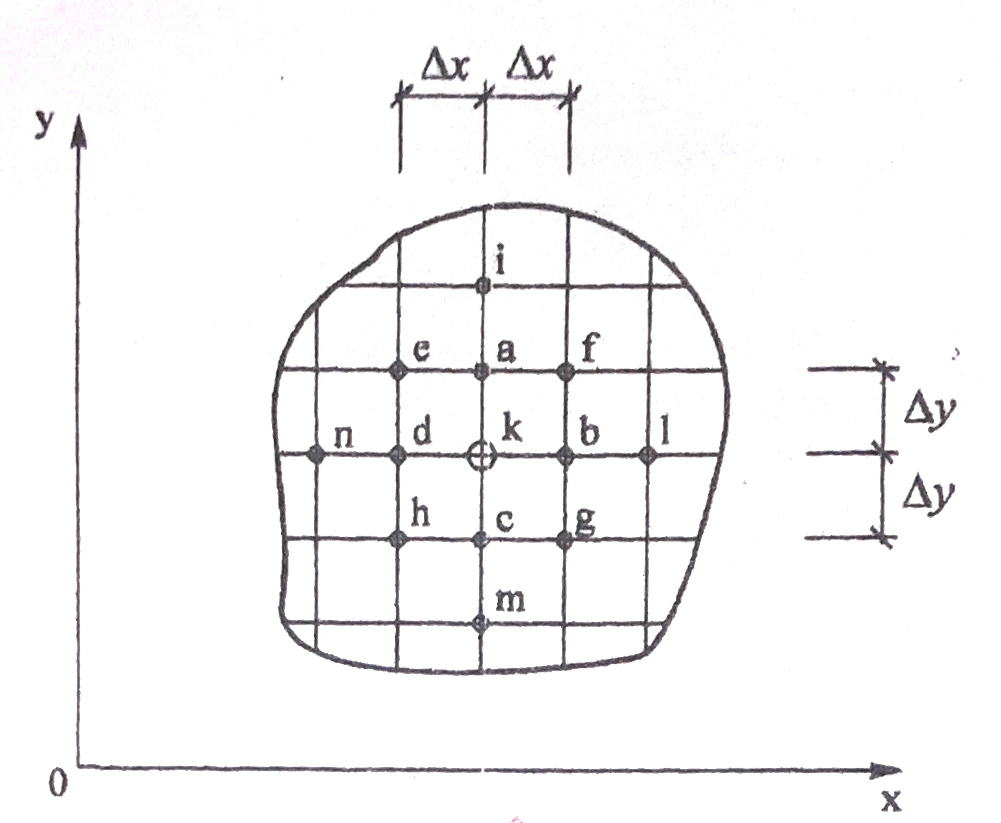
Рис.2.1

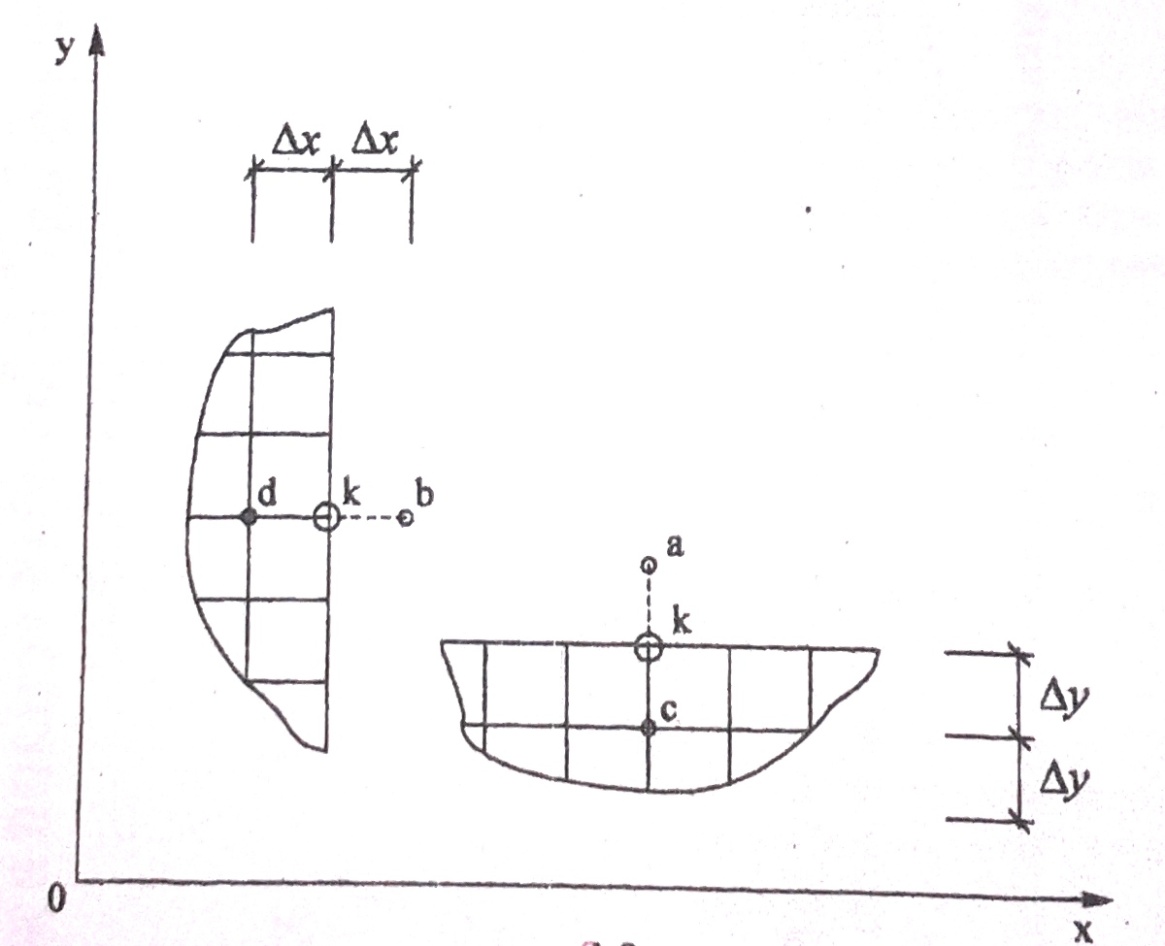
Для вузлів сітки, що містяться на контурі рами, значення функції напружень чисельно дорівнюють величинам згинальних моментів у відповідних перерізах замінюючої рами:

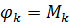(2.7)

Для позаконтурних вузлів (рис.2.2) функція напружень виражається згідно рамної аналогії через φ=φ(x,y) для передконтурних вузлів за формулою

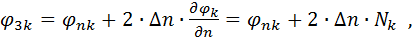(2.8)

де:

n – зовнішня нормаль (x або y);

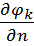– похідна від φ по нормалі (x або y);

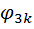– значення φ в позаконтурному вузлі;

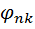– значення φ в передконтурному вузлі;

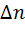- крок сітки у напрямку нормалі ( 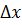для вертикальних граней та 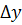для горизонтальних);

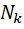– поздовжня сила у перерізі "К" стержня замінюючої рами. Правила знаків: згинальний момент вважається додатним, якщо розтягнуті внутрішні волокна стержнів замінюючої рами; повздовжня сила додатна, якщо вона спричиняє розтяг стержня.

Задача визначення контурних та поза контурних значень φ зводиться до побудови епюр згинальних моментів та повздовжніх сил у замінюючій рамі. Вибираючи замінюючи раму для розрахунку за програмою "ВИСОКА-БАЛКА", треба слідкувати за тим, щоб у стояках рами не виникали згинальні моменти. При відсутності бічного навантаження цього завжди можна домогтися, вибираючи раму статично визначеною з шарнірами в кутах.

Величини функції напружень у внутрішньоконтурних точках визначаються шляхом розв’язку системи скінчено-різницевих рівнянь. Напруження в усіх вузлах, включаючи контурні, можуть бути визначені за допомогою різницевих формул:

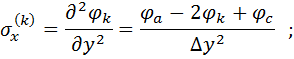
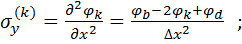(2.9)

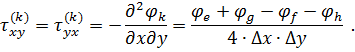
При виконанні деформаційної перевірки (сумісності деформацій) у напруженнях згідно з рівнянням сумісності деформацій у компонентах напруження:

(2.10)

де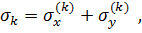

різницевий аналог для точки "К" (рис.2.1) має вигляд:

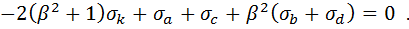(2.11)

Викладений алгоритм реалізовано в програмі "ВИСОКА-БАЛКА", складеної на кафедрі будівельної механіки для ПК.

Програма дозволяє створювати автоматичне формування системи скінчено-різницевих рівнянь. Система рівнянь зображується в матричному вигляді:

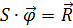(2.12)

У програмі прийнята така послідовність складання рівнянь: від лівої вертикальної грані спочатку для першого стовпчика внутрішніх вузлів зверху донизу, потім для наступного стовпчика в тому ж порядку і т.д. При дотримуванні вказаного порядку формування, матриця виявляється симетричною та набирає стрічкової структури.

Розв’язання системи (2.12) розшукується у вигляді:

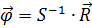(2.13)

Після цього за формулами (2.9) обчислюються напруження 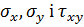, головні напруження :

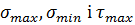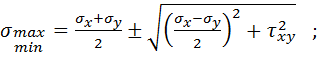(2.14)

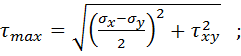
та кути нахилу головних площадок до осі х

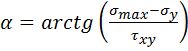(2.15)

1.3 Приклад розрахунку балки-стінки.

Потрібно розрахувати балку-стінку, зображену на рис.2.3.

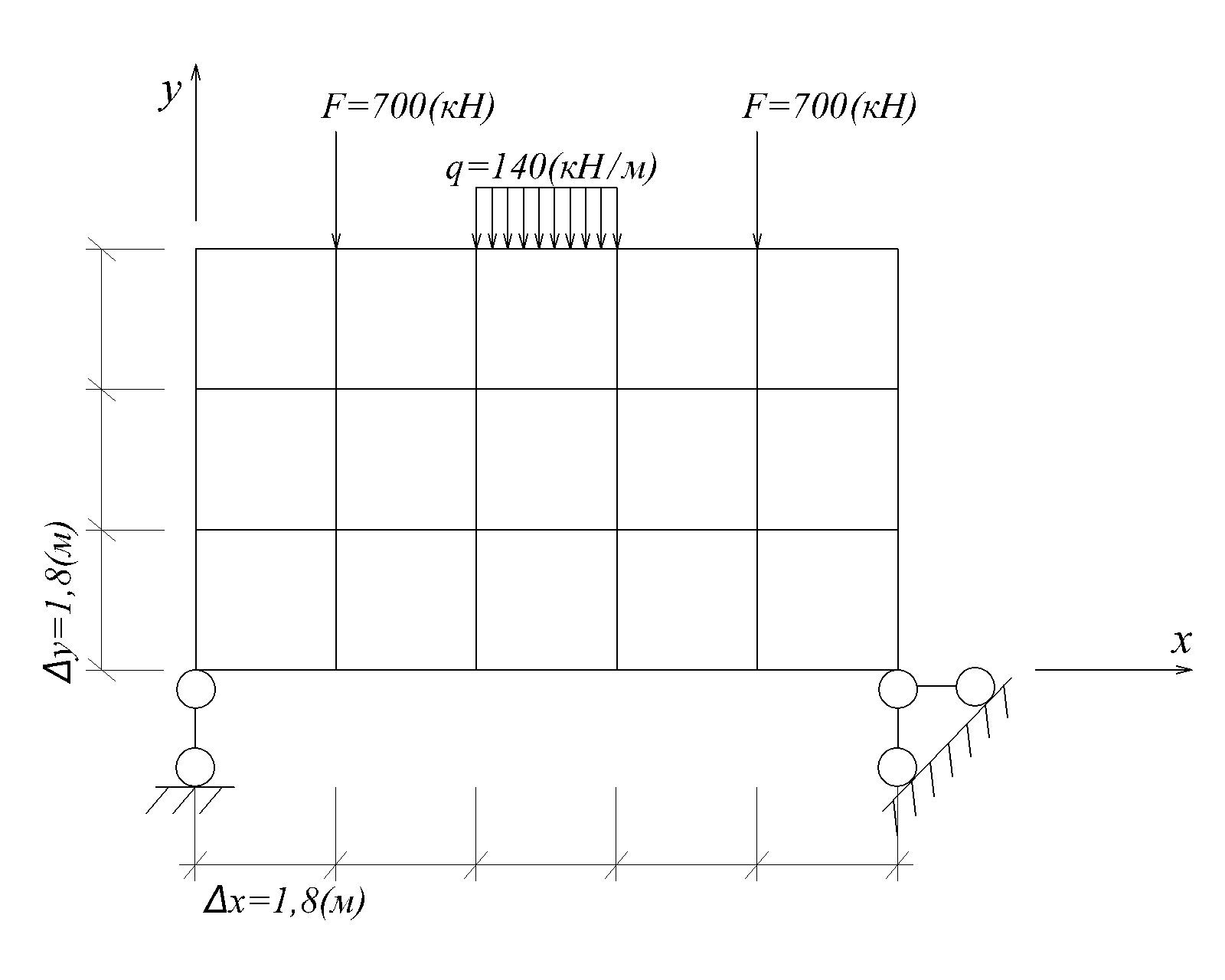
Рис.2.3

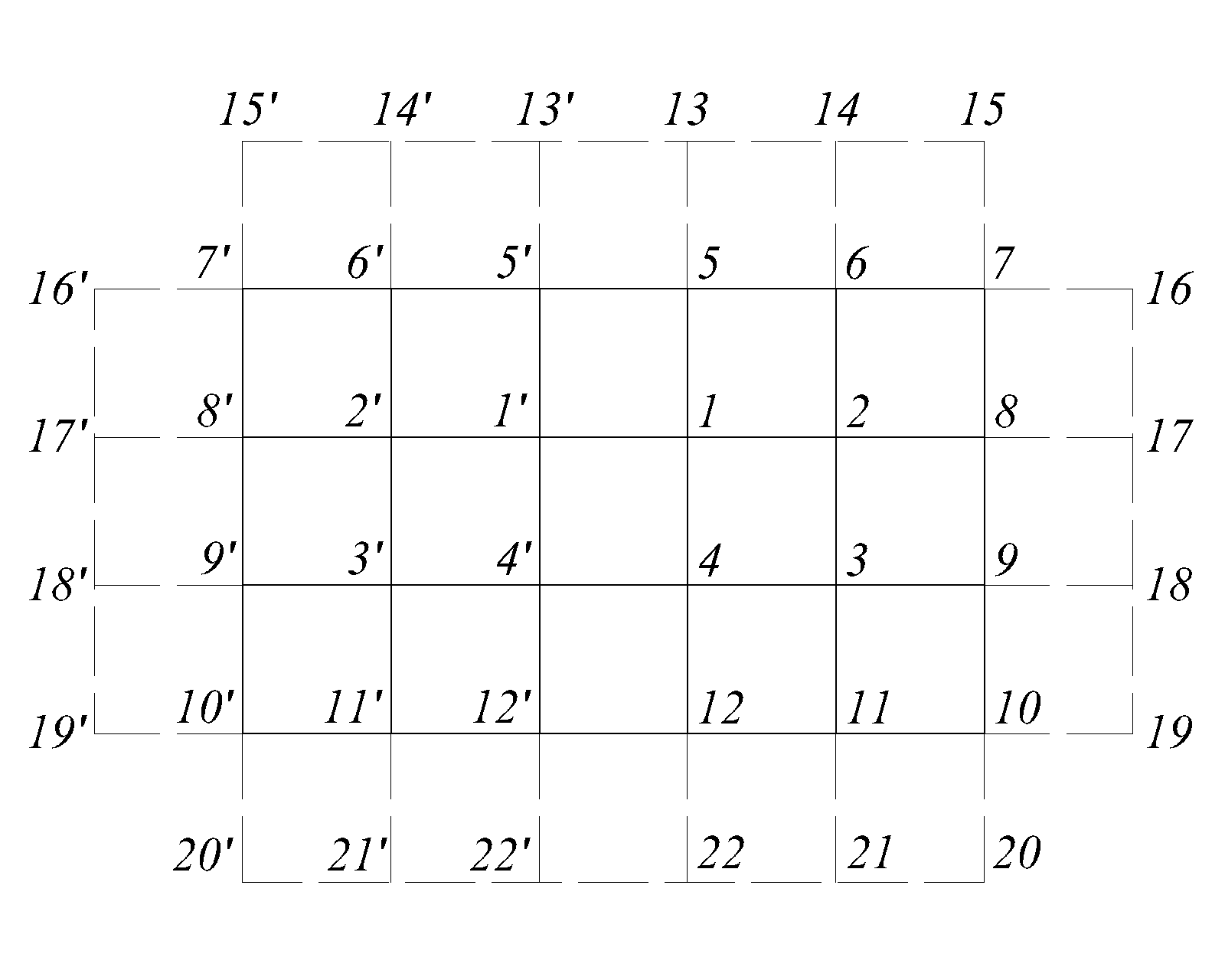
Рис.2.4

Задана квадратна сітка з розміром комірки 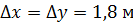. Наносимо контурну область та занумеруємо вузли сітки, приймаючи до уваги симетрію опорних закріплень й навантаження (рис.2.4) та визначення функції φ на контурі та за контуром за формулами (2.7) та (2.8) приймаємо раму з шарнірами в вузлах (рис.2.5) використовуючи принцип статичної визначуваності та геометричної незмінності.

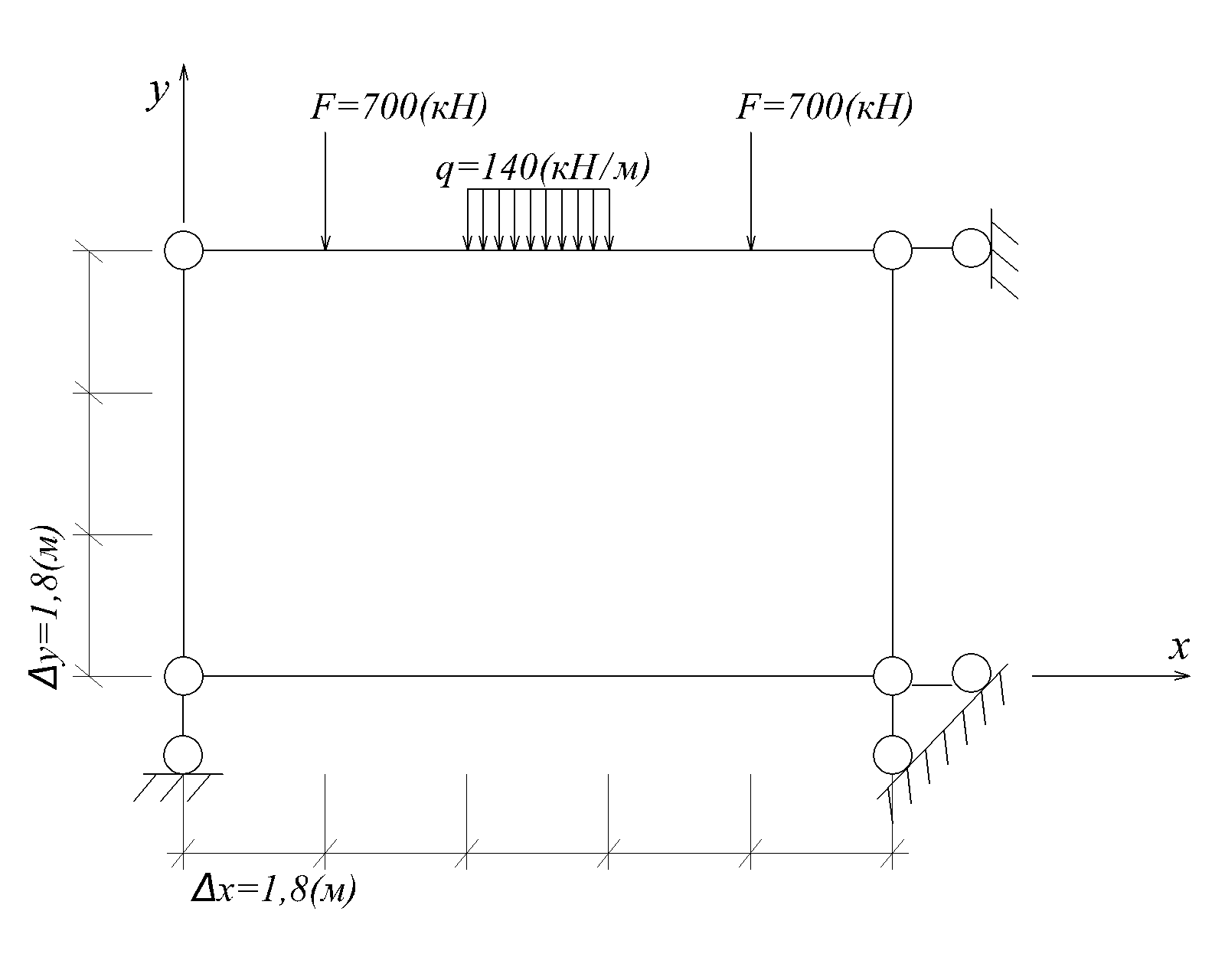
Рис.2.5

Будуємо для неї епюру згинальних моментів та поздовжніх сил. При цьому розрахувати можна окремо кожний стержень рами. При заданому навантаженні ригель розраховується тільки на згин, стояк тільки на центральний стиск.

1. Складаючи рівняння рівноваги, одержуємо опорні реакції:

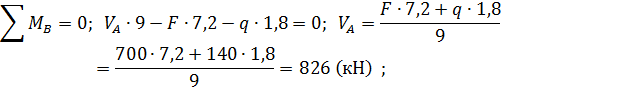
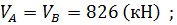
2. Визначаємо згинальні моменти та будуємо епюри.

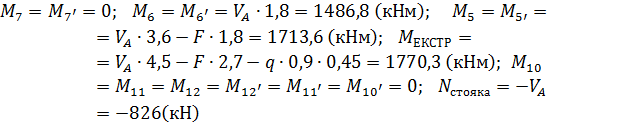
Будуємо епюри внутрішніх зусиль в рамі (рис.2.6)

Рис.2.6

Обчислення значень функцій напружень виконано в таблиці 1.

Таблиця 1.

Таблиця визначення функцій напружень

№ вузла	Порядок визначення	Визначення φ
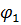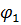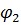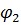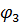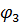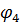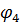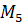		1713,6
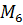		1486,8
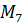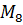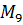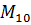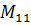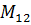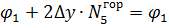		1347,513
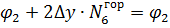		1087,807
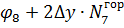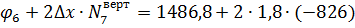		-1486,8
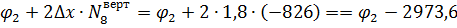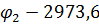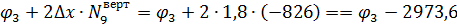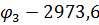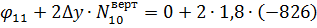		-2973,6

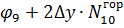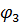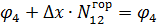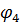Для вузлів 1-4 складемо алгебраїчні рівняння (2.6).

- вузол 1.

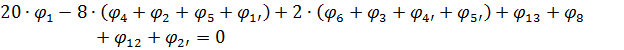
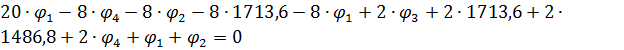
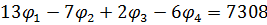
- вузол 2.

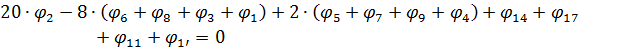
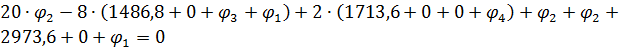
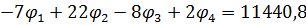
- вузол 3.

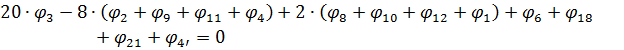
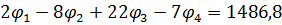
- вузол 4

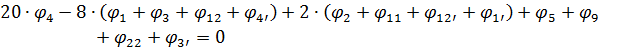
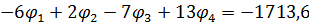
Системи алгебраїчних рівнянь:

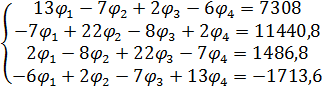
або у матричному вигляді:

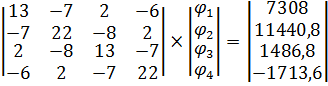
Розв'язуючи систему лінійних алгебраїчних рівнянь, одержуємо значення функцій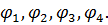

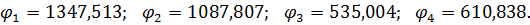
Перевіряємо правильність розв'язку рівнянь, підставивши в рівняння одержані 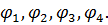Похибка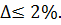

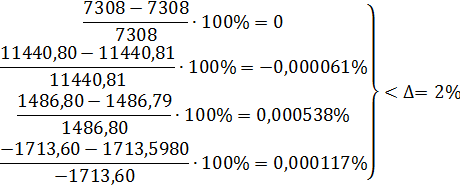
Значення функції напружень в вузлах різницевої сітки (рис.2.7).

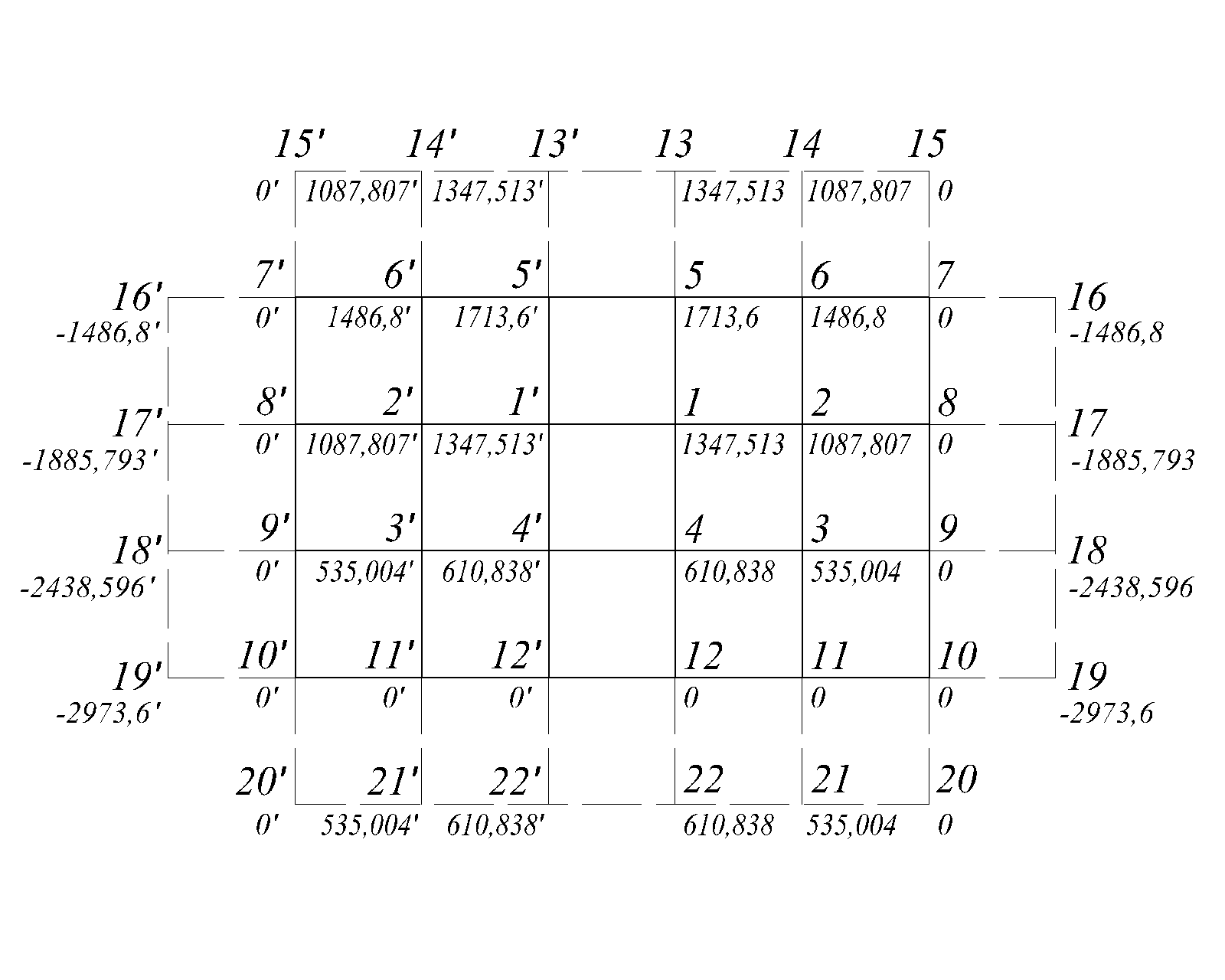
Рис.2.7

Величини напружень для вузлів посередині контуру та на контурі, обчислюються за формулами (2.9).

Знайдемо значення напружень у вузлах сітки.

- вузол 1.

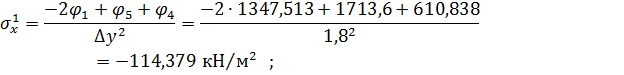
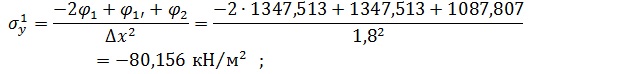
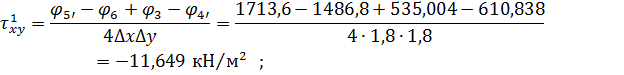
Вузол 2

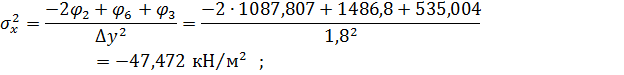
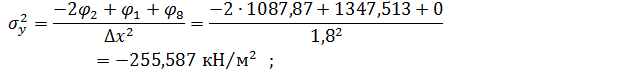
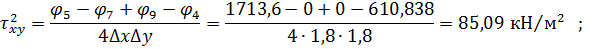
Вузол 3

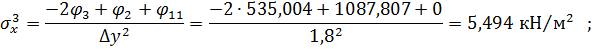
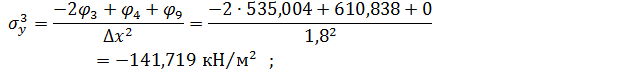
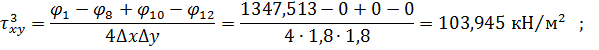
Вузол 4

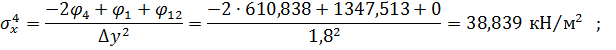
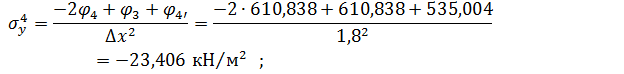
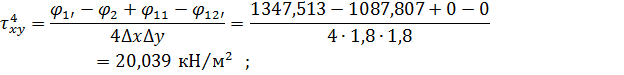
Решта значень напружень обчислюється таким же чином.

Напруження на контурі відповідають його навантаженню.

При заданому симетричному навантаженні епюри 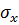та 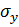симетричні відносно вертикальної осі, а епюри 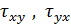- кососиметричні (рис.2.8).

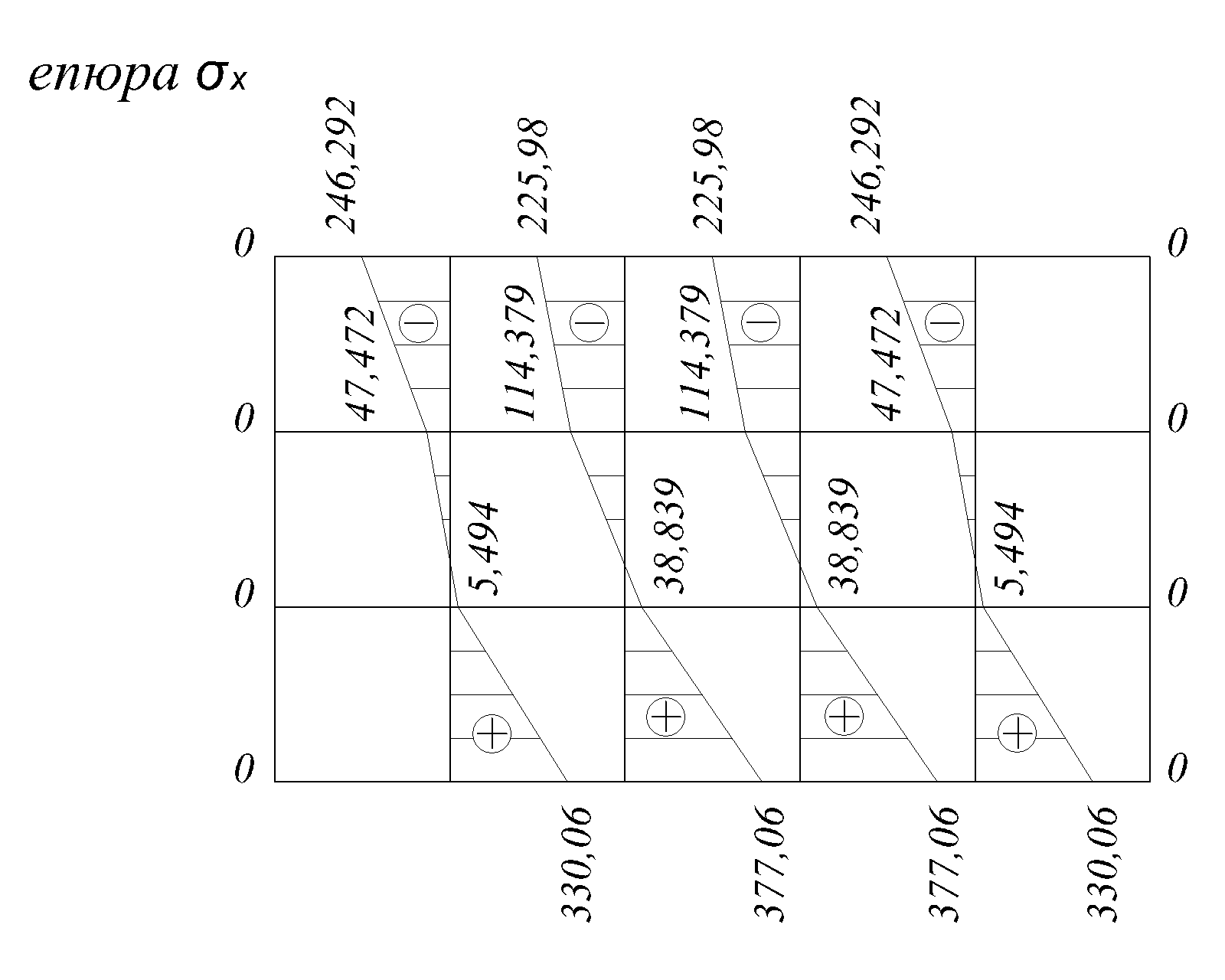
Рис.2.8.а

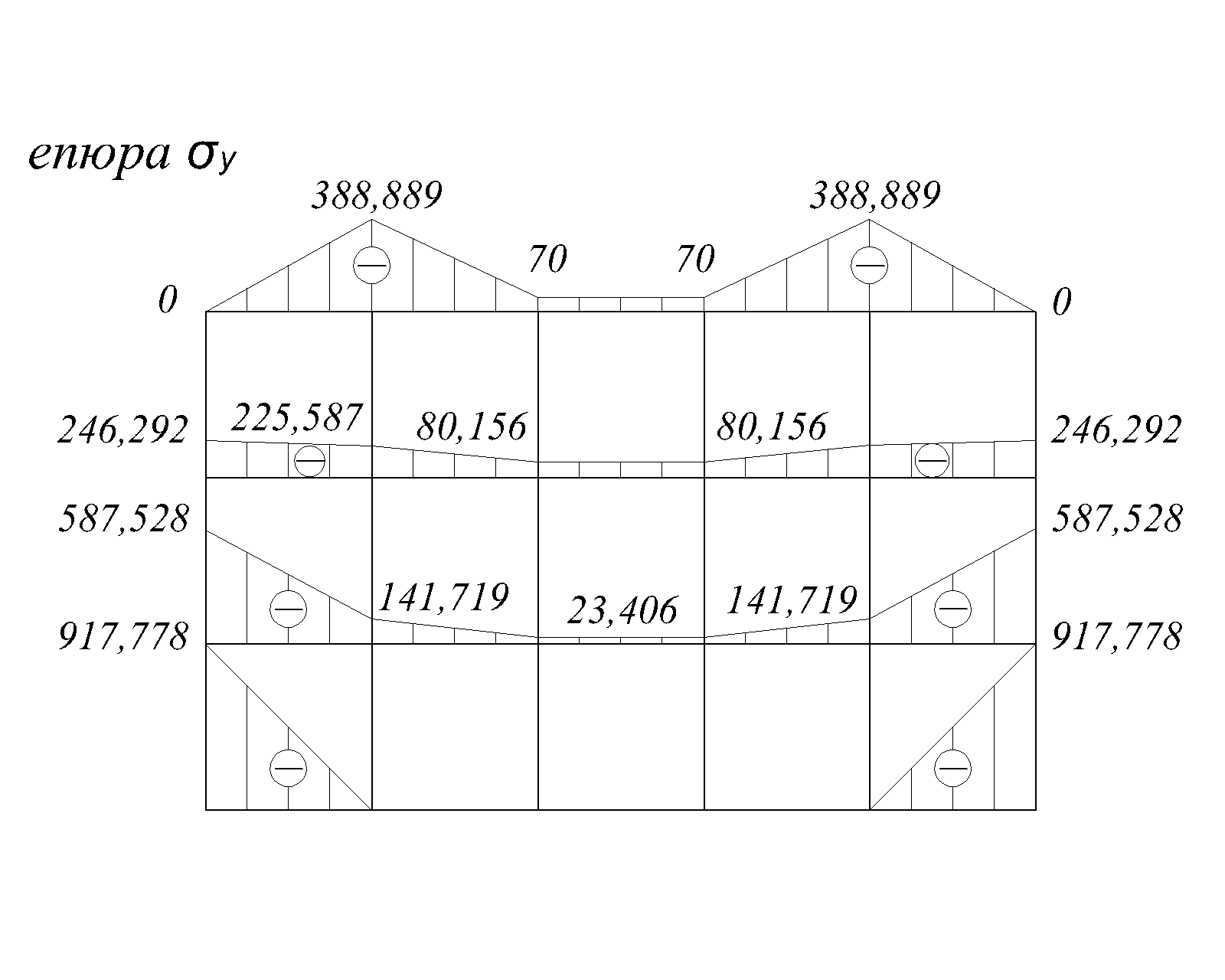
Рис.2.8.б

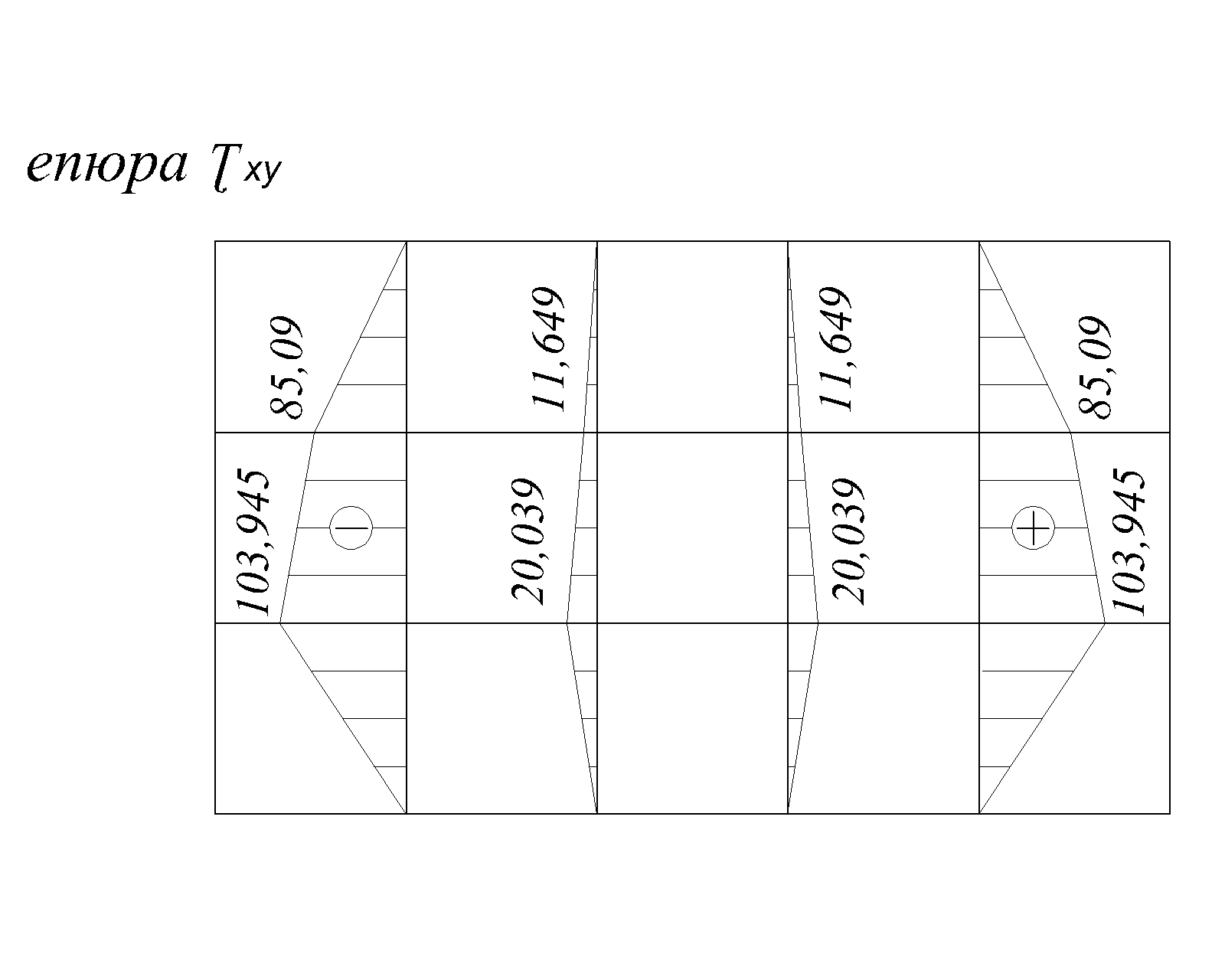
Рис.2.8.в

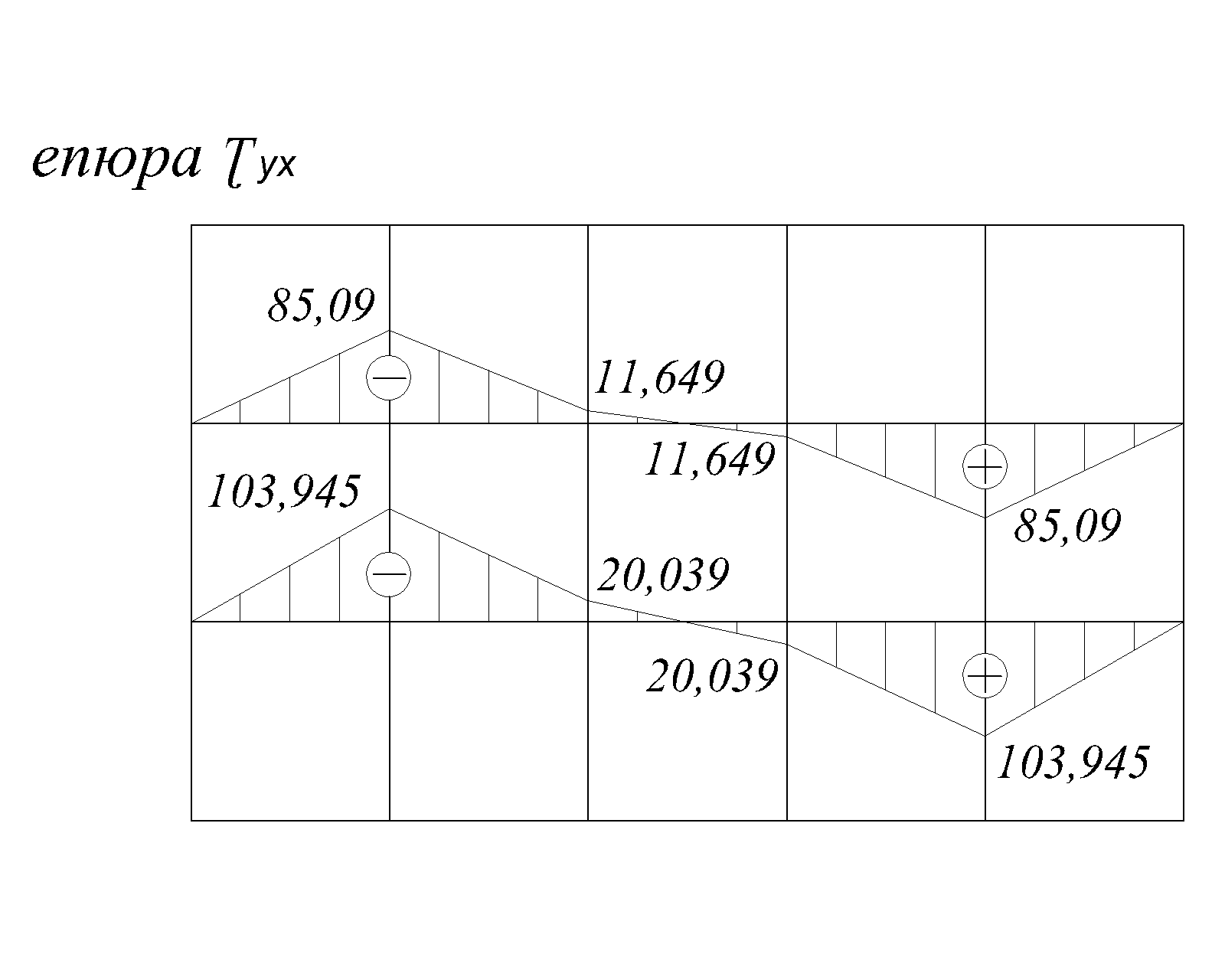
Рис.2.8.г

Статичні перевірки.

В вертикальних перерізах додатні та від'ємні площі епюри 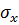повинні бути однакові ( повинна виконуватися умова ).

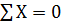Для перерізу 5-1-4-12:

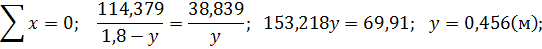
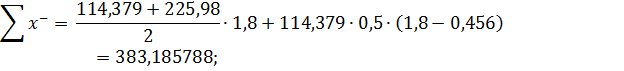
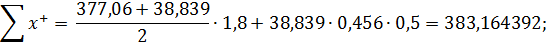
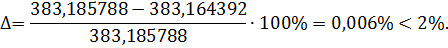
В горизонтальних перерізах площа епюри 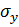повинна дорівнювати рівнодіючій зовнішнього навантаження, що випливає із умови .

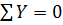Для перерізу 1-2-8:

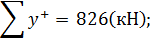
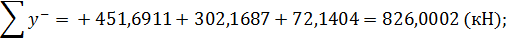
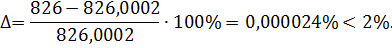
Деформаційна перевірка.

Необхідно перевірити виконання умови безперервності деформацій для внутрішніх точок балки стінки (2.11):

де 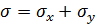– алгебраїчна сума напружень.

Для вузла №1.

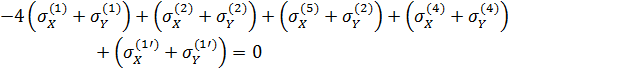
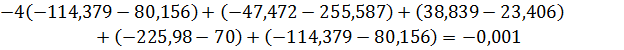
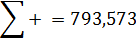
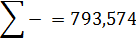
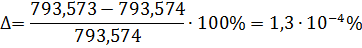
1.4 Стислий опис програми "ВИСОКА-БАЛКА"

1.4.1 Призначення програми.

Програма призначена для розрахунку балок-стінок за методом скінчених різниць при виконанні студентами РПР №1 зі спецкурсу "Чисельні методи" на ПК.

1.4.2 Технічна характеристика програми:

- операційна система – МАТЛАБ

- підготовка вихідних даних – згідно інструкції

- об’єм вихідної інформації – за прикладом

- видача результатів розрахунку – у табличній формі

1.4.3 Умовні позначення й ідентифікатори:

l – довжина балки-стінки;

h – висота балки-стінки;

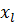- координата лівої опори;

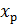- координата правої опори;

n – число вертикальних комірок сітки, ;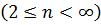

m - число горизонтальних комірок сітки, ;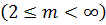

vvR – число зосереджених сил на верхньому ригелі k=1…vvR;

uvR – число рівномірно розподілених сил на верхньому ригелі p=1…uvR;

FvR(k) – значення сил, що діють на верхньому ригелі;

xvR(k) – координата сили, прикладеної до верхнього ригеля;

qvR(p) – значення рівномірно розподіленого навантаження на верхньому ригелі;

nacqvR(p) – координата початку рівномірно розподіленого навантаження на верхньому ригелі;

konqvR(p) – координата кінця рівномірно розподіленого навантаження на верхньому ригелі;

vnR – число сил на нижньому ригелі kn=1…vnR;

unR – число рівномірно розподіленого навантаження на верхньому ригелі pn=1…unR;

FnR(kn) – значення сил, прикладених до нижнього ригеля;

xnR(kn) – координата сили, прикладеної до нижнього ригеля;

qnR(pn) – значення рівномірно розподіленого навантаження на нижньому ригелі;

nacqnR(pn) – координата початку рівномірно розподіленого навантаження на нижньому ригелі;

konqnR(pn) – координата кінця рівномірно розподіленої сили на нижньому ригелі;

Fk – масив значень функції напружень у вузлах скінчено-різницевої сітки;

Sigx – масив значень напружень 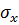у вузлах сітки;

Sigy – масив значень напружень 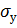у вузлах сітки;

Taxy – масив значень дотичних напружень 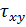у вузлах сітки;

Sigmax - масив значень напружень 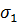у вузлах сітки;

Sigmin - масив значень напружень 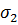у вузлах сітки;

Tamax – масив значень дотичних напружень 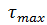у вузлах сітки;

Def – масив значень з результатами деформаційної перевірки;

alfa – масив значень кутів нахилу головних площадок до осі X. (в градусах)

1.4.4 Результати розрахунку.

Результати розрахунку роздруковуються у вигляді таблиць у командній зоні екрану, або у вигляді файлів у робочій зоні екрану.

1.4.5 Приклад підготовки вихідних даних.

Для роботи з програмою необхідно підготувати вихідні дані стосовно кількості і різноманітності навантаження. Для цього необхідно накреслити "схематично" балку-стінку і показати основні характеристики, приведені в пункті 1.4.3 та на рис.2.9.

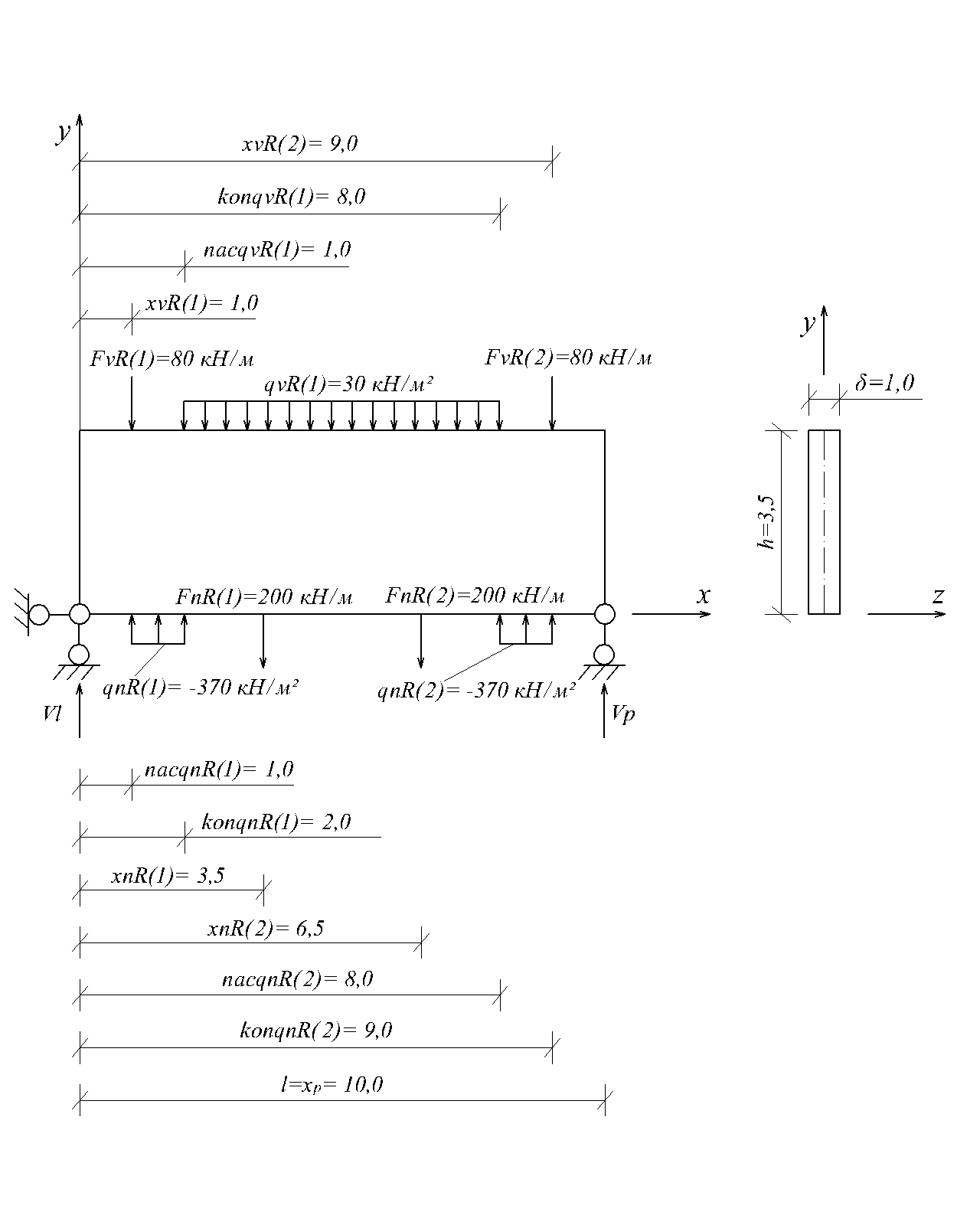
Рис.2.9

1.5 Приклад розрахунку балки-стінки за допомогою ПК.

Треба розрахувати балку-стінку одиничної товщини, зображену на рис.2.3.

Показуємо геометричні характеристики балки-стінки, положення та значення навантаження, діючого на балку-стінку (рис.2.10).

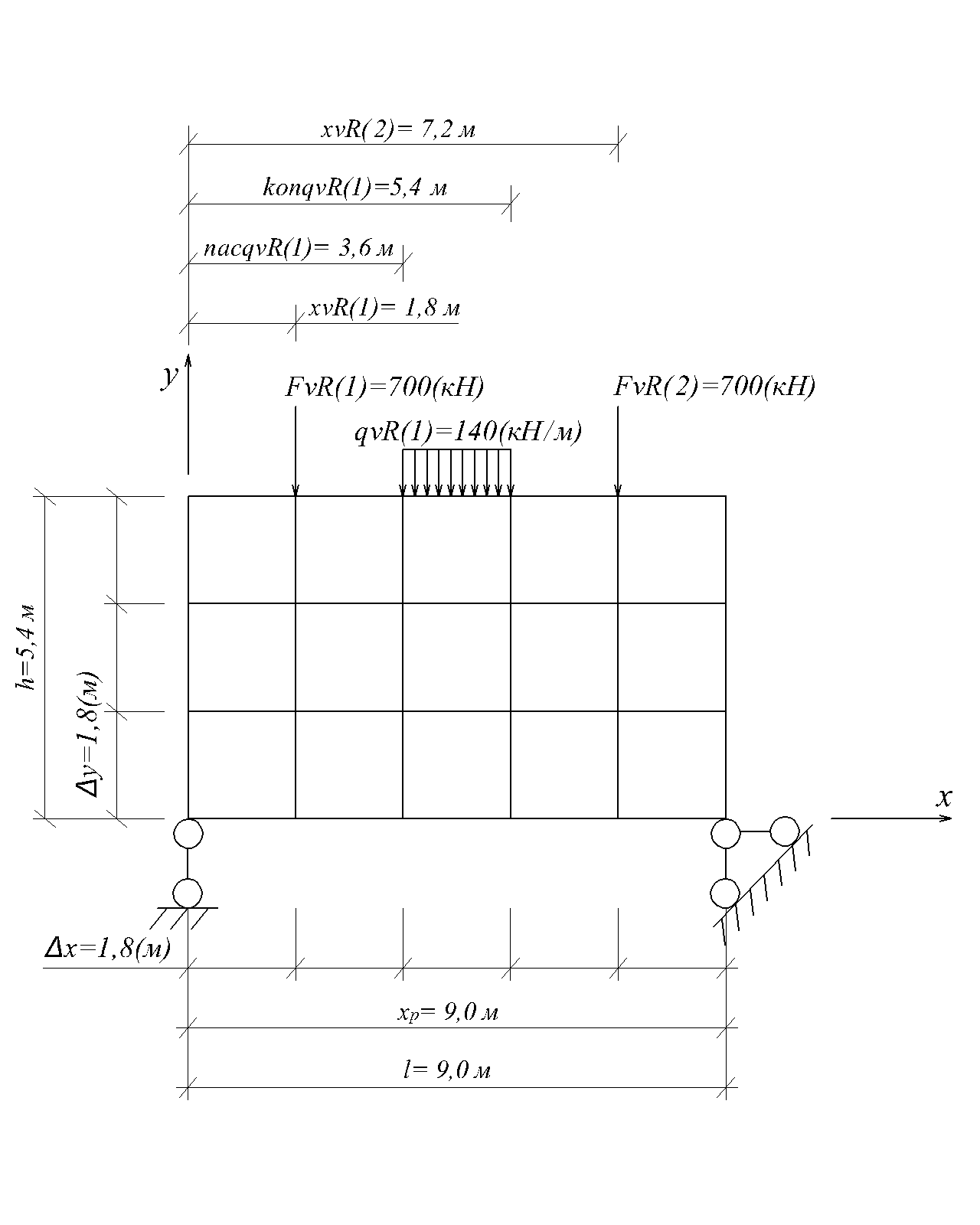
Рис.2.10

Довжина балки-стінки:

l = 9 м;

Висота балки-стінки:

h = 5,4 м;

Координата лівої опори:

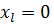м;

Координата правої опори:

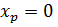м;

Задаємо кількість комірок по горизонталі та по вертикалі:

m=5;

n=3;

Число зосереджених сил на верхньому ригелі:

vvR=2;

Число рівномірно розподілених навантажень на верхньому ригелі:

uvR=1;

Значення сил, діючих на верхньому ригелі:

FvR(1)=700 кН;

FvR(2)=700 кН;

Координати сил, діючих на нижньому ригелі:

xvR(1)=1.8 м;

xvR(2)=7.2 м;

Значення рівномірно розподіленого навантаження на нижньому ригелі:

qvR(1)=140 ;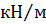

Координата початку рівномірно розподіленого навантаження на верхньому ригелі:

nacqvR(1)=3.6 м;

Координата кінця рівномірно розподіленого навантаження на верхньому ригелі:

konqvR(1)=5.4 м;

Система алгебраїчних рівнянь у матричному вигляді, автоматично формується програмою:

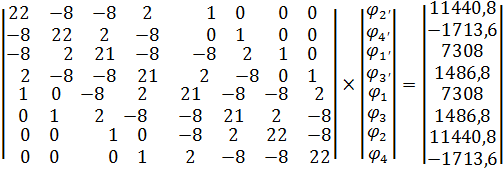
Fk – масив значень функції напружень у вузлах скінчено-різницевої сітки;

		1087.81	1347.51	1347.51	1087.81
-1486.80		1486.80	1713.60	1713.60	1486.80		-1486.80
-1885.79		1087.81	1347.51	1347.51	1087.81		-1885.79
-2438.60		535.00	610.84	610.84	535.00		-2438.60
-2973.60							-2973.60
		353.00	610.84	610.84	353.00

Sigx – масив значень напружень 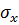у вузлах сітки;

	-246.29	-225.98	-225.98	-246.29
	-47.47	-114.38	-114.38	-47.47
	5.49	38.84	38.84	5.49
	330.25	377.06	377.06	330.25

Sigy – масив значень напружень 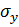у вузлах сітки;

	-388.89	-70.00	-70.00	-388.89
-246.29	-255.59	-80.16	-80.16	-255.59	-246.29
-587.53	-141.72	-23.41	-23.41	-141.72	-587.53
-917.78					-917.78

Taxy – масив значень дотичних напружень 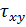у вузлах сітки;

	-85.09	-11.65	11.65	85.09
	-103.97	-20.04	20.04	103.97

Def – масив значень з результатами деформаційної перевірки;

-1.5951e-013	-3.4802e-013	-1.4501e-013	1.6966e-012
1.7691e-012	2.1751e-013	-8.8455e-013	1.1601e-013

Порівняємо результати розрахунку без застосування ПК та на ПК.

Для вузла №1.

	Значення	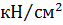Похибка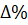
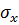	114,379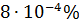
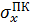	114,38
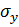	-80,156	0,005%
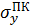	-80,16
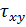	11,649	0,009%
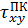	11,65

Збільшимо число комірок в п'ять разів.

m=25;

n=15;

Поверхня функцій напружень має вигляд (рис.2.11).

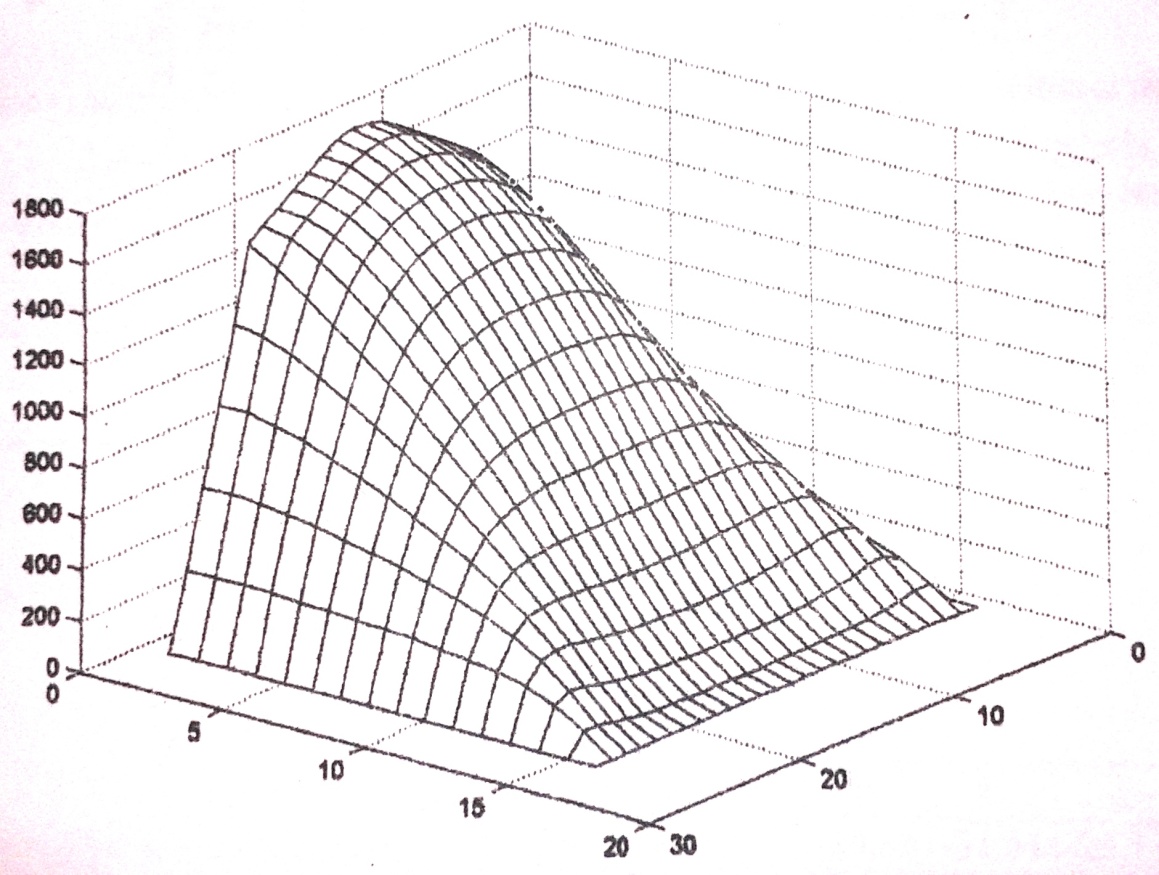
Рис.2.11

Sigx – масив значень напружень 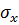у вузлах сітки з кроком перерізу 1,8м по горизонталі;

	-1104.92	-230.64	-230.64	-1104.92
	-90.69	-233.16	-233.16	-90.69
	-5.83	-224.29	-224.29	-5.83
	-15.34	-203.38	-203.38	-15.34
	-26.83	-175.97	-175.97	-26.83
	-36.25	-145.99	-145.99	-36.25
	-45.44	-114.44	-114.44	-45.44
	-54.52	-80.23	-80.23	-54.52
	-61.90	-41.08	-41.08	-61.90
	-63.98	5.64	5.64	-63.98
	-53.79	62.36	62.36	-53.79
	-19.01	130.54	130.54	-19.01
	59.36	209.98	209.98	59.36
	203.75	298.02	298.02	203.75
	423.59	389.23	389.23	423.59
	678.69	476.17	476.17	678.69

Sigy – масив значень напружень 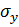у вузлах сітки з кроком перерізу 1,8м по вертикалі; (показано масив значень для половини вузлів, оскільки балка-стінка має симетричне навантаження)

-212.08	-247.66	-269.79	-286.41	-297.02
-923.67	-714.90	-481.01	-294.43	-169.48
-4588.89

→

-1944.44	-0.00	0.00
-286.78	-239.26	-177.00	-122.50
-93.84	-50.38	-25.72	-11.51

→

-0.00	-70.00	-140.00	-140.00
-85.41	-65.36	-56.92	-54.28
-3.15	1.74	4.44	5.64

→

Taxy – масив значень дотичних напружень 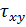у вузлах сітки з кроком перерізу 1,8м по горизонталі;

	-33.17	-38.26	38.26	33.17
	-63.05	-37.91	37.91	63.05
	-91.24	-32.19	32.19	91.24
	-117.08	-30.10	30.10	117.08
	-139.42	-31.51	31.51	139.42
	-157.11	-33.84	33.84	157.11
	-168.83	-34.64	34.64	168.83
	-172.61	-32.33	32.33	172.61
	-165.52	-26.38	26.38	165.52
	-143.69	-17.26	17.26	143.69
	-103.65	-6.56	6.56	103.65
	-46.22	3.23	-3.23	46.22
	15.62	9.04	-9.04	-15.62
	47.57	8.27	-8.27	-47.57

Tayx – масив значень дотичних напружень 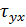у вузлах сітки з кроком переріза 1,8м по вертикалі; (показано масив значень для половини вузлів, так як балка-стінка має симетричне навантаження)

	-90.42	-151.66	-181.81	-176.69
	-175.04	-240.43	-231.70	-190.80

→

-139.42	-93.62	-62.25	-46.47
-143.69	-102.01	-69.33	-45.46

→

-38.66	-31.51	-21.18	-7.49
-28.76	-17.26	-9.14	-2.85

→

Після отримання таблиць результатів розрахунку, будуємо епюри напружень 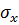, 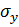і 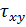, для тих же перерізів що і в прикладі №1.

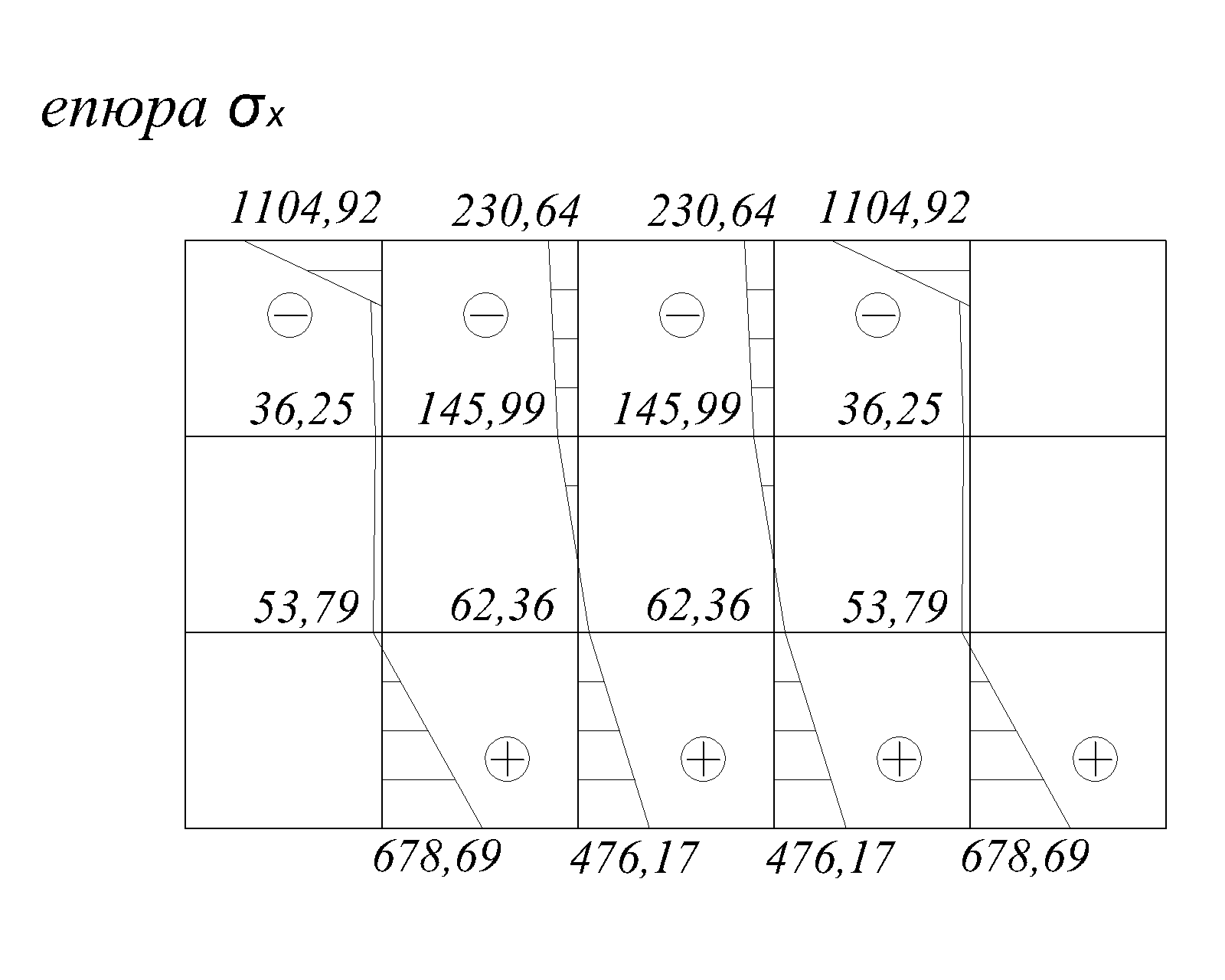
Рис.2.12а

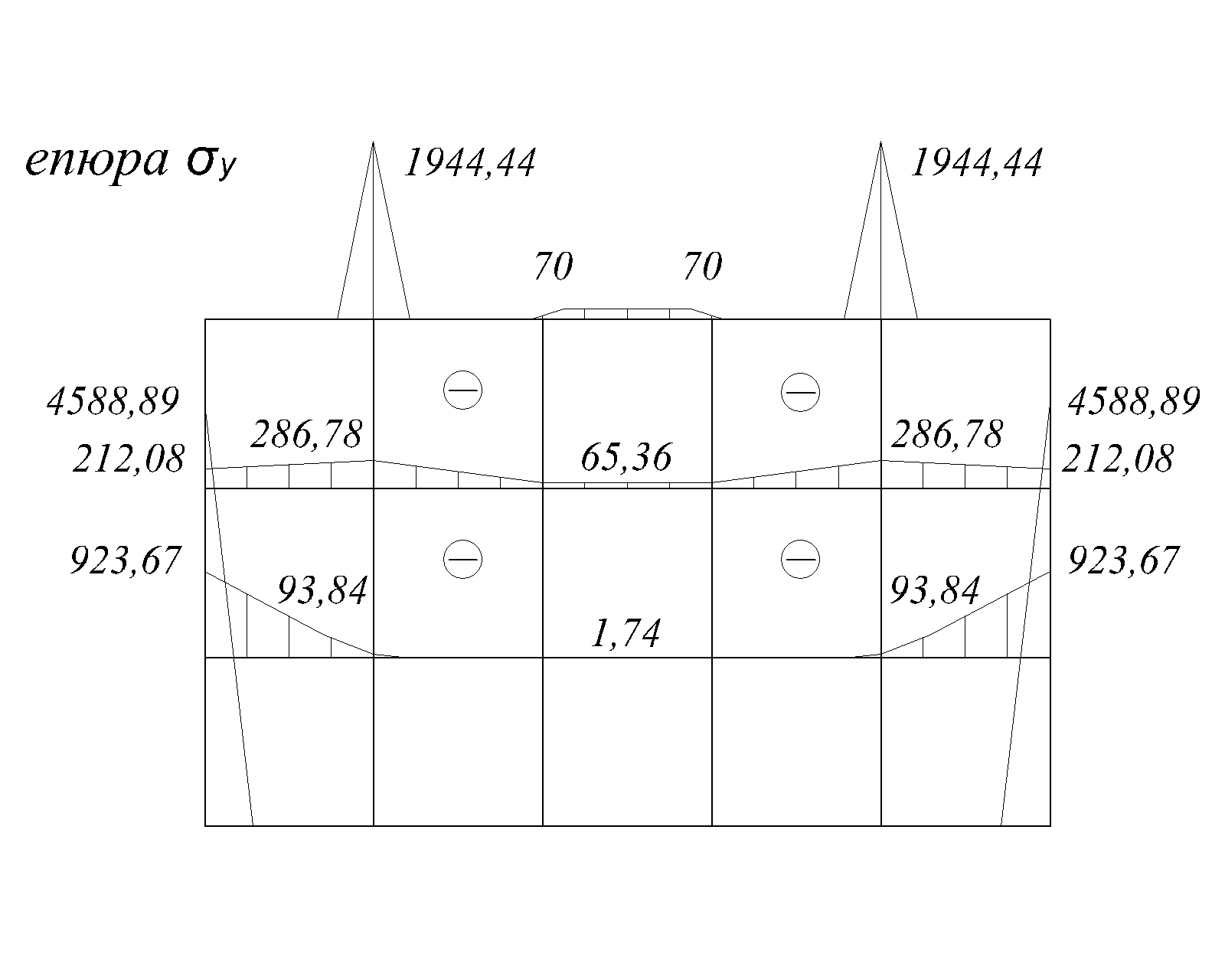
Рис.2.12б

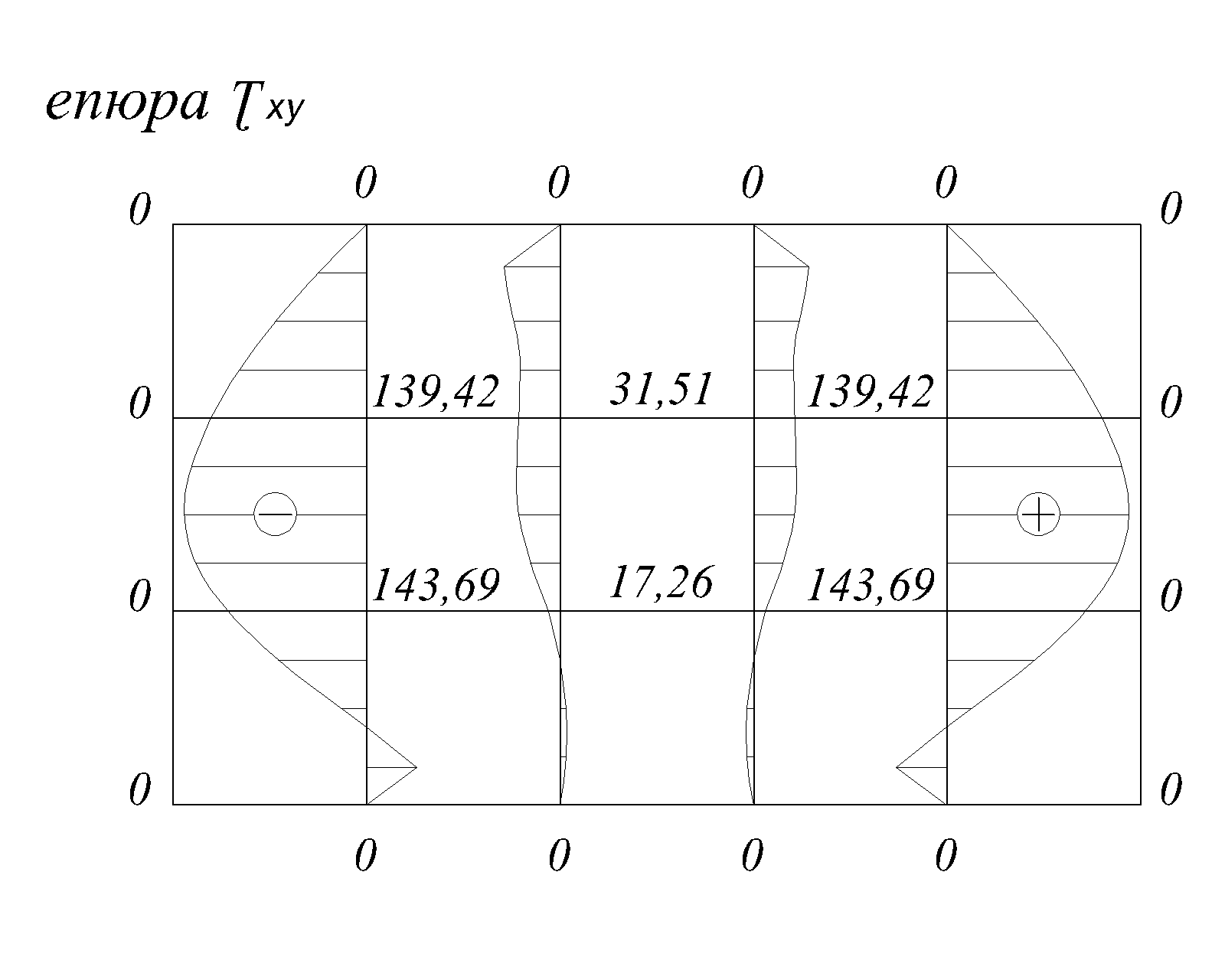
Рис.2.12в

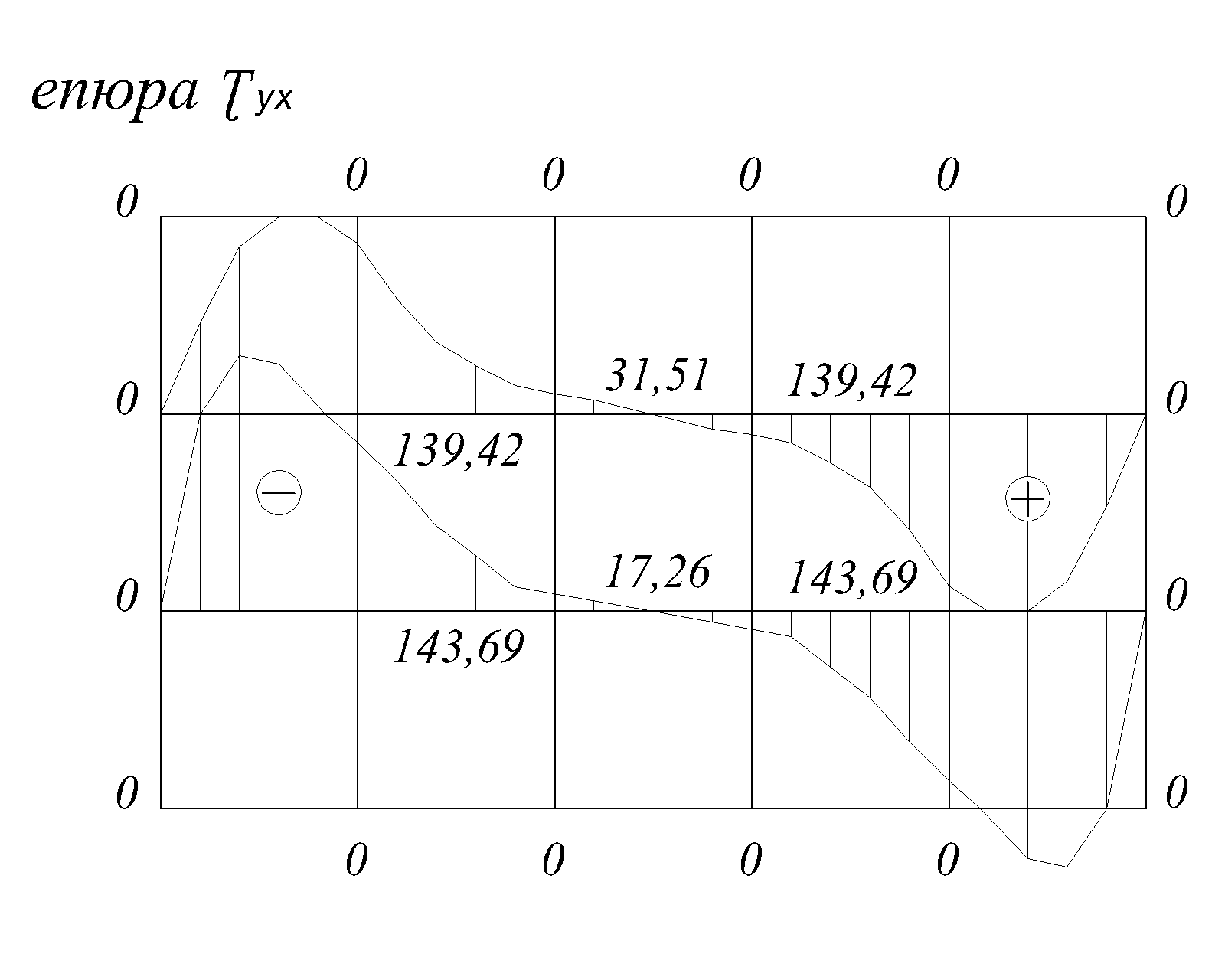
Рис.2.12г

Порівняємо результати розрахунку на ПК для 5х3 та 25х15 перерізів.

Для вузла №1.

	Значення	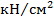Похибка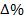
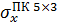	114,38	27,63%
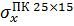	145,99
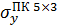	-80,16	22,64%
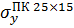	-65,36
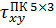	11,65	170,47%
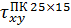	31,51

Порівнюючи результати бачимо, що при зменшенні розмірів комірки в п'ять разів точність розрахунку підвищується доволі суттєво.

1.6 Контрольні запитання

1. Поясніть, що таке узагальнений плоский напружений стан (УПНС) і запишіть тензори напружень та деформацій.

2. Поясніть, що таке плоска деформація (ПД), і запишіть тензори напружень та деформацій.

3. Покажіть схему напружень, що виникають в нескінченно малому елементі диска. Запишіть диференціальні рівняння рівноваги для плоскої задачі та поясніть значення всіх величин, що входять до цих рівнянь.

4. Запишіть геометричні рівняння Коші для плоскої задачі та поясніть значення всіх величин, що входять до рівнянь.

5. Запишіть рівняння закону Гука для УПНС і ПД. Поясніть значення всіх величин, що входять до рівнянь.

6. Запишіть рівняння нерозривності (сумісності) деформацій у компонентах деформації. З яких рівнянь воно здобуто?

7. Запишіть рівняння нерозривності (сумісності) в напруженнях. З яких залежностей воно здобуто?

8. Які існують типи граничних умов і чим вони відрізняються?

9. Що таке функція напружень? Як вона зв'язана з напруженнями?

10. Як здобуто скінчено-різницеве рівняння, що відповідають бігармонічному рівнянню плоскої задачі?

11. Як визначаються значення функції напружень в контурних та позаконтурних вузлах?

12. Що таке рамна аналогія?

13. Як зв'язана функція напружень φ з напруженнями 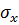, 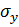і 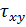при розрахунку балок-стінок за методом скінчених різниць?

14. Як виконується деформаційна перевірка розрахунку балок-стінок за методом скінчених різниці?

1.7 Додаток №1

Таблиця №2.

Цифра шифру	Перша цифра шифру	Друга цифра шифру	Третя цифра шифру
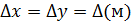	P (кН)	q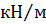
№ схеми	№ нав-ня
	1,0
	1,1
	1,2
	1,3
	1,4
	1,5
	1,6
	1,7
	1,8
	2,0

Таблиця №3.

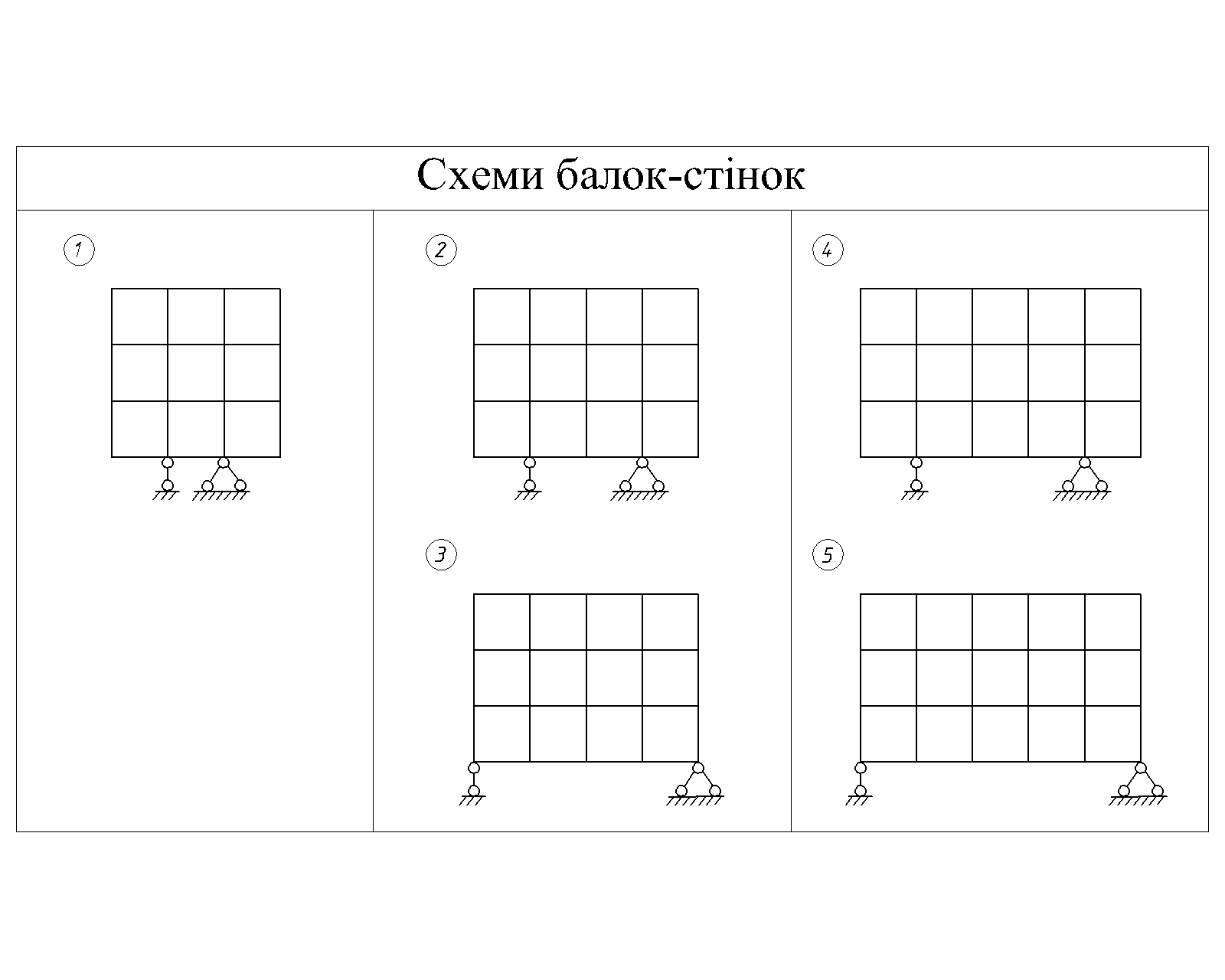
Таблиця №4.

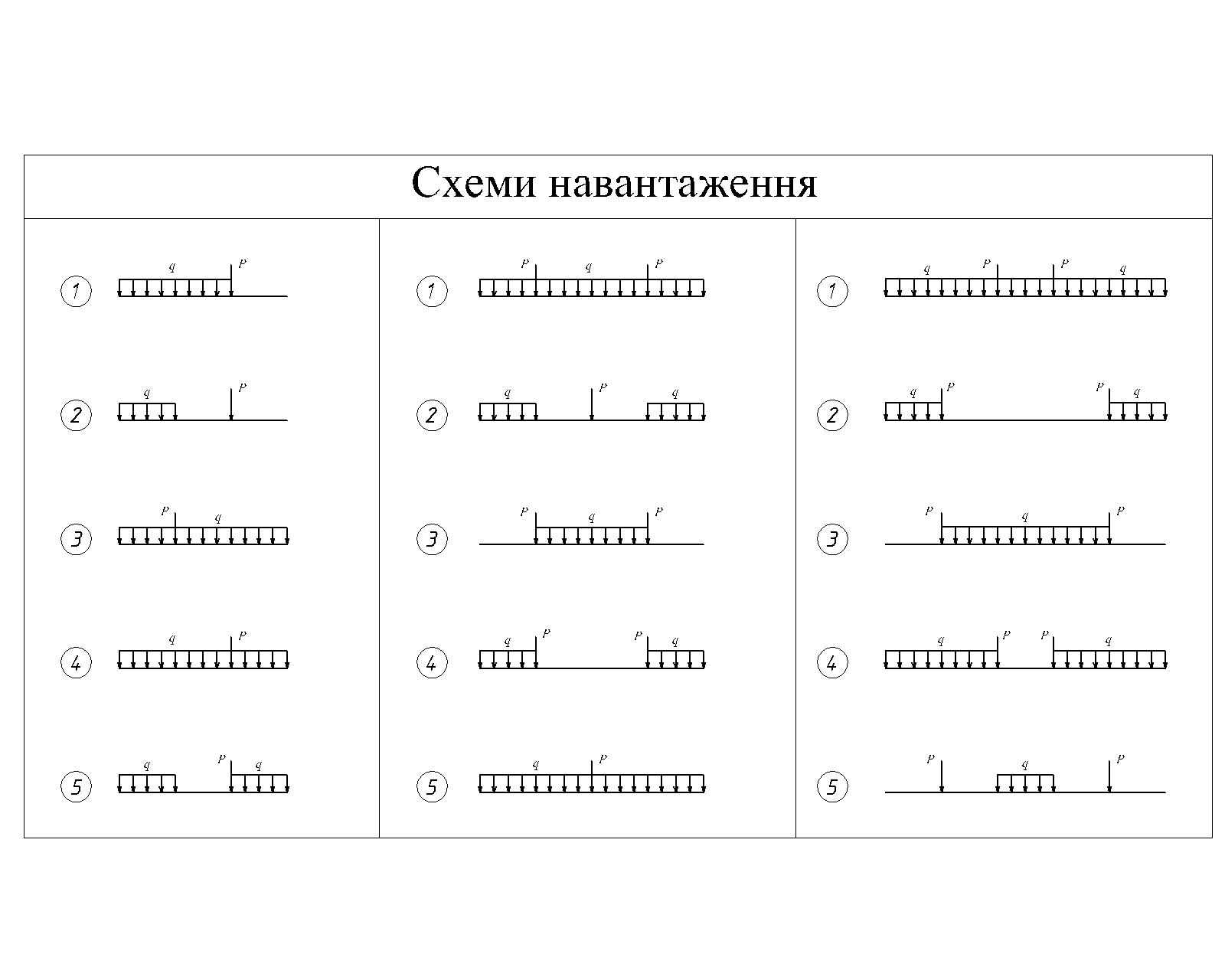
Література:

1. Яременко А.Ф., Балдук П.Г. Механика материалов и конструкцій. – Одесса, 2001, - 25/с.

2. Жемочкин Б.Н. Теория упругости. Госстройиздат, М., 1957.

3. Киселев В.А. Плоская задача теории упругости. М., "Высшая школа", 1976.