С различными импедансами. Согласование импедансов

Рассмотрим две среды с импедансами (волновыми сопротивлениями) Z₁ =r₁ с₁ и Z₂ =r₂ с₂, граница раздела сред имеет координату x = 0 (рис. 1-30). Волна (1) падает из первой среды. На границе раздела сред наблюдается отражение волны (2) и прохождение волны (3) во вторую среду.

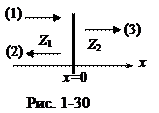
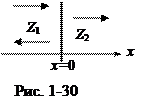Соответствующие уравнения волны в средах:

x₁ = a₁ 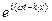; x₂ = a₂ 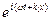; x₃ = a₃ 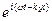, где k₁ и k₂ - волновые числа в первой и второй среде соответственно.

Задача стоит в определении соотношения амплитуд этих волн при заданных волновых сопротивлениях сред.

На границе раздела сред смещение частиц среды справа и слева одинаково. Кроме того, силы T 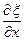, действующие на элементы среды слева и справа, должны быть одинаковыми. В противном случае элементы среды приобретут бесконечное ускорение. Итак, из граничных условий получим следующие уравнения:

x₁ + x₂ = x₃; T 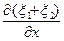= T .

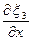Подставим в эти граничные условия уравнения волн, получим:

a₁ + a₂ = a₃; (31)

- k₁Ta₁ + k₁Ta₂ = - k₂Ta₃. (31^*)

Но k₁ = 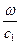, k₂ = 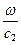, Z₁ =r₁ с₁ = 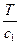, Z₂ =r₂ с₂ = 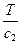. Поэтому (31^*) запишется в виде соотношения: Z₁(a₁ - a₂) = Z₂ a₃. (32)

Из уравнений (31) и (32) получим соотношения между амплитудами волн:

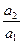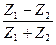= - коэффициент отражения по амплитуде;

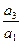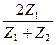= - коэффициент пропускания по амплитуде.

При Z₂ = ¥ (например, конец закрепленной струны)

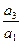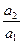= 0 и = -1,

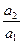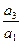т.е. прошедшей волны нет, отраженная волна бежит со сдвигом фазы на p радиан относительно падающей волны. При Z₂ = 0 (например, свободный конец кнута) = 1, = 2.

Определим энергетические коэффициенты отражения и прохождения. Например, отрезок струны единичной массы r начинает совершать колебания с приходом волны, максимальная энергия которой равна максимальной кинетической энергии E = 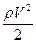= 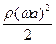Скорость переноса энергии в волне Ec = 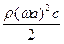= 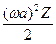. Имеем:

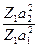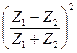= - энергетический коэффициент отражения;

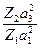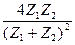= - энергетический коэффициент прохождения.

При Z₁ = Z₂ энергия не отражается, т.е. импедансы сред согласованы.

Вопрос согласования импедансов имеет большое практическое значение. Например, для нормальной работы приемной аппаратуры необходимо согласование между входом приемника и антенной; согласование разного рода соединений в аппаратуре. Впрочем, рассогласование импедансов также имеет практическое применение. Например, в акустических методах контроля изделий обнаружение дефектов основывается на разности импедансов материала изделия и дефектов. Именно на дефектах наблюдается отражение зондирующих акустических сигналов из-за разности импедансов материала изделия и дефектов.

Итак, задача состоит в согласовании импедансов двух сред Z₁ =r₁ с₁ и Z₁ =r₃ с₃ с помощью третьей среды с импедансом Z₂ =r₂ с₂, который поместим между средами Z₁и Z₁ (рис.1-31). Условие согласования запишется в виде

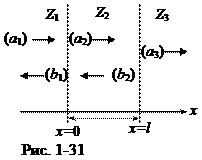
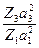= 1. (33)

Выпишем уравнения прошедших и отраженных волн: x₁ = a₁ 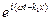; x₂ = a₂ 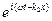; x₃ = a₃ ;

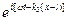x₄ = b₁ 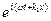; x₂ = b₂ .

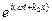Воспользуемся граничными условиями для непрерывности смещения и сил при x = 0 и x = l , а также условием (33), после несложных, но довольно громоздких вычислений получаем условие согласования импедансов:

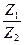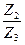= (или Z₂ = 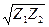) и l = 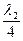, где l₂ = .

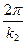1.2.5. Волновой пакет

А. Волны, характеризуемые одной частотой и длиной волны, называются монохроматическими волнами. Монохроматическая волна является идеализацией, реальные волны состоят их группы (пакета) частотных гармоник. Например, пакет из двух волн x₁ и x₂ одинаковой амплитуды и близкими частотами w₁ и w₂ образуют так называемое биение амплитуды результирующей волны:

x₁ + x₂ = a cos(w₁t - k₁x) + a cos(w₂t - k₂x) =

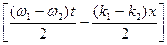= 2a cos cos .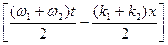

Член 2acos 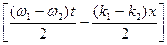указывает, что амплитуда волны модулирована в пространстве и времени, медленно изменяясь с частотной (w₁ - w₂)/2 и волновым числом (k₁ - k₂)/2. Максимальная амплитуда равна 2a. Скорость пакета в отсутствии дисперсии, т.е. когда фазовые скорости компонентов пакета с разными частотами одинаковы w₁/k₁ = w₂/k₂, равна

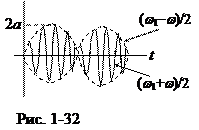
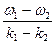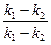= c = c.

На рис. 1-32 показаны колебания среды в некоторой ее точке со временем. Аналогичный рисунок имеет профиль волны в пространстве в фиксированный момент времени.

Групповая скорость волнового пакета – это скорость распространения максимальной амплитуды пакета. При близких частотах v_гр. = 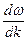= = 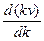v - .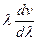

При 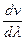> 0 наблюдается нормальная дисперсия, когда v_гр.< v. Ситуация, когда 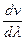< 0, называется аномальной дисперсией. При аномальной дисперсии наблюдается сильное поглощение энергии волны.

Б.Рассмотрим волновой пакет, состоящий из большой группы n частотных компонент в частотном диапазоне пакета Dw = w - w₁. Для простоты расчета, амплитуды компонент будем считать одинаковыми и равными a.

Пусть соседние по частоте компоненты отличаются на dw, тогда частотный диапазон Dw = w - w₁ = ndw. В точке среды x = 0 колебания частиц среды в поле волны будет выражаться суммой

x(t)_x=0 = a cosw₁t + a cos(w₁ + dw)t + a cos(w₁ + 2dw)t +… a cos[w₁ + (n - 1)dw]t .

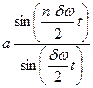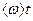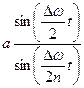Соседние по частоте компоненты отличаются по фазе на величину dwt радиан и имеют одинаковые амплитуды. Поэтому данную сумму можно рассчитать, не прибегая к методу Фурье, а используя метод векторной диаграммы, т.е. геометрически складывая равные по модулю n векторов, которые повернуты относительно друг друга на один и тот же угол dwt. В результате сложения, получим: x(t)_x=0 = cos = cos ,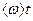

где 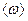= w₁ + 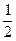(n - 1) dw - средняя частота диапазона Dw. При больших значенияхn уравнение для x(t)_x=0 можно записать в виде:

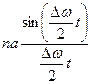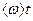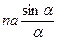x(t)_x=0 = cos = cos 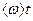, где a = .

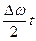В момент времени t = 0 фазаa = 0, т.е. в этот момент 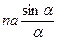= na, т.к. при этом 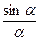® 1. Амплитуда при t = 0 максимальна. С течением времени фаза a изменяется. Допустим, за время Dt фаза изменилась от нуля до p :

a = 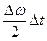= p . (34)

В этом случае амплитуда равна нулю и промежуток времени 2Dt (ноль амплитуды получается и ранее при a = -p) может служить мерой ширины импульса пакета. Точнее, мерой ширины служит Dt, т.к. ширину считают на уровне половины максимальной амплитуды na/2.

Из (34) получаем соотношение:

Dn Dt = 1, т.к. Dw = 2p Dn . (34^*)

Полученное соотношение (34^*) называется теоремой о ширине частотной полосы волнового пакета. В частности, из (34^*) следует, что чем короче во времени импульс, тем шире диапазон частот Dn импульса. При Dn = 0 (монохроматическая волна) длительность импульса стремится к бесконечности.

1.2.6. Затухание реальных волн в среде

A. При распространении упругой волны в среде всегда происходит поглощение энергии, переносимое волной. Механизм потерь энергии обусловлены процессами переноса – теплопроводностью, диффузией, вязкостью. В качестве примера получим дифференциальное уравнение диффузии (уравнение Фика), описывающее динамику этого процесса переноса. Для простоты рассмотрим одномерную задачу. Предварительно получим, исходя из закона сохранения массы, уравнение непрерывности массы среды dm = r dx на прямой 0x. Здесь r - линейная плотность среды.

Скорость потока v = 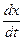и за время dt через левый конец прямой пройдет масса rvdt = qdt, через правый конец - (q + ¶q)dt. Изменение массы в интервале длины dx за время dt будет ¶(dm) = - ¶q dt. Разделим это выражение на dx dt и перенесем все члены в одну сторону, получим уравнение непрерывности:

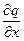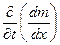+ = 0 или 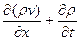= 0.

Феноменологическое уравнение диффузии (закон Фика) имеет вид:

q = - c ,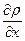

где 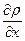- градиент плотности среды; c -коэффициент диффузии.

Подставим закон Фика в уравнение непрерывности, получим дифференциальное уравнение диффузии:

= .

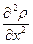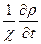В главе «Тепловые поля» получено аналогичное уравнение для явления теплопроводности (уравнениеФурье-Кирхгофа), которое для одномерного случая имеет вид: 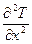= 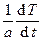, где a – коэффициент температуропроводности. Аналогичные уравнения получаются и для других явлений переноса, связанные с переносом массы, импульса, энергии. Подчеркнем, явления переноса на микроскопическом уровне носят случайный характер, что и обусловливает потери энергии волны.

Б.Итак, уравнения, определяющие потери энергии волны в среде вследствие разных механизмов потерь, можно записать виде общего дифференциального уравнения переноса

= .

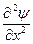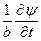При незначительных потерях энергии, т.е. когда расстояние, на которое распространяется, много больше длины волны, дифференциальное уравнение распространения можно записать в виде комбинации волнового уравнения и дифференциального уравнения переноса:

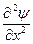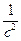
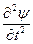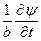= + . (35)

Решение уравнения будем искать в виде y =y₀ 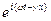. Подставим это уравнение в (35), получим комплексное значение g :

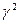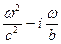= = k² .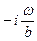

Величина g - комплексное число, поэтому можно представить это число в виде: g = k - ia. Имеем соотношение 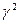» k² 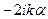, если a << k. Таким образом, решение (35) принимает вид:

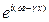y =y₀ = y₀ 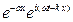. (36)

Амплитуда волны является функцией координаты y₀ 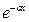. С увеличением расстояния от излучателя, амплитуда волны уменьшается по экспоненте. Коэффициент поглощения имеет размерность обратной длины, следовательно, можно записать, что a = 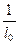, где l₀ - расстояние в среде, по прохождении которого амплитуда волны уменьшается в е » 2,7 раз.

АКУСТИЧЕСКОЕ ПОЛЕ