Метод Тейлора первого порядка

Министерство образования Российской Федерации

Воронежский государственный университет

Математический факультет

Численные методы решения обыкновенных дифференциальных уравнений

Методические указания

по курсу «Методы вычислений»

для студентов IV-V курсов

всех форм обучения

Составитель В.П.Трофимов

Воронеж

2002 г.

Настоящие методические указания предназначены для выполнения лабораторной работы «Численные методы решения обыкновенных дифференциальных уравнений» по курсу «Методы вычислений» студентами IV-V курсов дневного и вечернего отделений математического факультета. Разработка может быть использована для самостоятельной работы студентов и подготовке к экзамену.

Разработка представляет собой существенно переработанный и дополненный вариант методических указаний .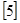

Литература.

1. Бахвалов Н.С., Лапин А.В., Чижонков Е.В. Численные методы в задачах и упражнениях. / Под ред. В.А.Садовничего: Учеб. пособие.– М.: Высш. шк., 2000. – 190 с.

2. Арушанян И.О., Чижонков Е.В. Материалы семинарских занятий по курсу «Методы вычислений» / Под ред. О.Б.Арушаняна: Учеб. пособие. – 2-е изд. – М.: Изд-во ЦПИ при механико-математическом ф-те МГУ, 1999. – 96 с.

3. Плис А.И., Сливина Н.А. Лабораторный практикум по высшей математике: Учеб. пособие для втузов. – 2-е изд., перераб. и доп. – М.: Высш. шк., 1994. – 416 с.

4. Хайрер Э., Нёрсетт С., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи: Пер. с англ. – М.: Мир, 1990. – 512 с.

5. Аброськина Г.С., Трофимов В.П. Методические указания по методам вычислений и вычислительной практике. Часть III: - Воронеж.: ВГУ, 1989. – 24 с.

1. Постановка задачи.

Пусть требуется найти дифференцируемую при 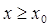функцию 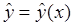, удовлетворяющую дифференциальному уравнению при 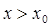и начальному условию при :

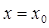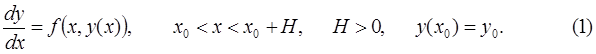
Будем считать, что правая часть дифференциального уравнения 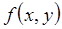удовлетворяет условиям теоремы существования и единственности решения 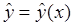задачи Коши (1).

Численное решение задачи (1) состоит в построении таблицы приближенных значений 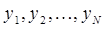точного решения 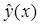в точках 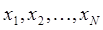отрезка 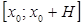. При этом величину 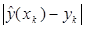называют локальной алгоритмической ошибкой численного метода при 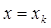. В реальных вычислениях всегда присутствует ошибка округления и фактически будут вычислены .

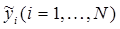Существует множество методов решения задачи Коши (1). Мы рассмотрим два важнейших класса численных методов: методы, основанные на разложении решения в ряд Тейлора, и методы полиномиальной аппроксимации.

Выберем 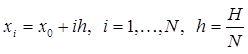. Точки 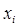называются узлами сетки, а величина 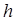- шагом сетки.

2. Метод Тейлора.

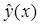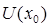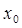Предполагая, что точное решение задачи (1) является аналитической функцией в некоторой окрестности точки , разложим 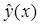в ряд Тейлора в точке :

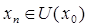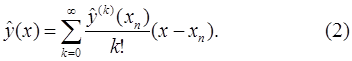
Заметим, что 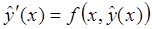и, следовательно,

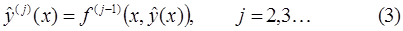
Производные 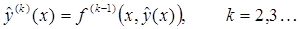вычисляются по правилам дифференцирования сложной функции:

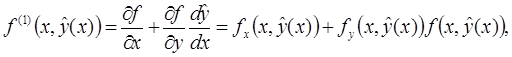
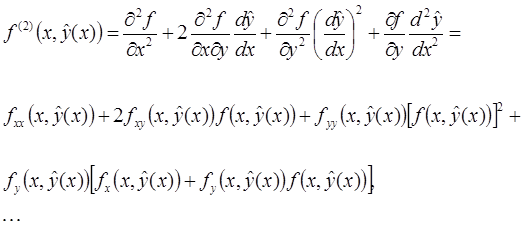
Используя (3), перепишем (2) при 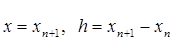, в виде:

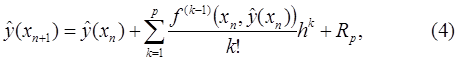
где 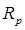- члены высших порядков. Заменив в (4) 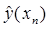на 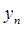и отбросив 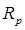, получим алгоритм метода Тейлора

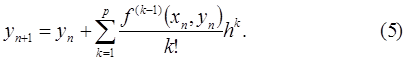
Обычно алгоритм (5) записывают в виде:

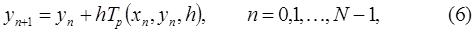
где

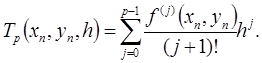
Метод (6) называют методом Тейлора порядка .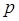

Замечания:

1. Для метода Тейлора порядка 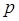остаточный член 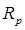в формуле (4) имеет вид 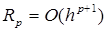при 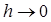. Следовательно, если в алгоритме (6) 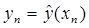, то локальная алгоритмическая ошибка метода имеет порядок .

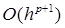2. Общее количество шагов численного решения задачи (1) на отрезке 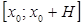определяется отношением 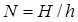. При заданной точности приближенного решения число шагов 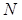уменьшается с увеличением порядка 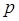метода Тейлора. Но увеличение порядка метода приводит к росту числа членов в формуле (7). Для численной реализации алгоритма (6) нужно вычислять 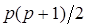значений функции 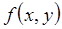и всех ее частных производных 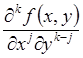при 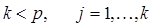. Вычисление большого числа частных производных является трудной задачей. Поэтому методы Тейлора выше четвертого порядка в вычислительной практике обычно не используются.

Метод Тейлора первого порядка.

Из формулы (6) при 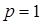получаем

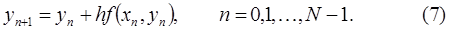
Этот алгоритм называется явным методом Эйлера.Здесь 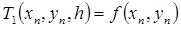.