Задача об использовании сырья

Постановка задачи. Построить обобщенную математическую модель для определения максимальной прибыли предприятия от изготовления (N) видов продукции из (К) видов сырья. Пусть а_ij – количество i-го сырья, расходуемого на единицу j-й продукции, а b_i – количество сырья. Обозначим с_j прибыль от единицы j-й продукции. Следует воспользоваться обозначениями и данными задачи об использовании сырья из подраздела 3.7. Варианты заданий представлены в табл. 5.17.

Таблица 2

Вариант задания

Номер варианта	Задача 7	Задача 8
N	K	M	L

В табл.2 N – число видов продукции, K – число видов сырья, M – число видов отливок, L – число машин.

Решение постановки задачи №2:

Для составления математической модели введем обозначения: а_ij – количество i-го сырья, расходуемого на единицу j-й продукции, а b_i – количество сырья, с_j прибыль от единицы j-й продукции, П_j- вид продукции.

Шаг 1: определение максимальной прибыли предприятия от изготовления (N) видов продукции из (К) видов сырья произведем в соответствии со следующей таблицей.

запас сырья	П1	П2	П3	П4	П5
b1	a11	a12	a13	a14	a15
b2	a21	a22	a23	a24	a25
b3	a31	a32	a33	a34	a35

а₁₁ – количество сырья В1, расходуемого на единицу продукции П1.

а_ij – количество i-го сырья, расходуемого на единицу j-й продукции ,

b1,b2,b3-количества сырья на складе, из которого предприятие изготавливает три вида продукции.

Шаг 2: Для составления математической модели введем обозначения:

Пусть: Х1- это количество продукции П1,изготавляемого на предприятии;

Х2- это количество продукции П2,изготавляемого на предприятии;

Х3- это количество продукции П3,изготавляемого на предприятии;

Тогда: а11х1-количество сырья b1 необходимое, для изготовление продукции П1;

а21х1-количество сырья b2 необходимое, для изготовление продукции П1;

а31х1-количество сырья b3 необходимое, для изготовление продукции П1;

а1jхi-количество сырья b1 необходимое, для изготовление продукции Пi;

а2jхi-количество сырья b2 необходимое, для изготовление продукции Пi;

а3jхi-количество сырья b3 необходимое, для изготовление продукции Пi;

а12х2-количество сырья П1 необходимое, для изготовление продукции П2;

а12хi-количество сырья П1 необходимое, для изготовление продукции Пi;

Шаг 3. Составим условия ограничения запасов сырья.

Количество сырья необходимое для изготовления всех видов продукции на предприятии будет равно:

а11∙х1+а12∙х2+а13∙х3+ а14∙х4+ а15∙х5

Тогда баланс по сырью вида В1 может быть записан в виде неравенства :

а11∙х1+а12∙х2+а13∙х3+ а14∙х4+ а15∙х5 ≤ В1

Аналогично для остальных видов сырья.

а21∙х1+а22∙х2+а23∙х3+ а24∙х4+ а25∙х5 ≤ В2

а31∙х1+а32∙х2+а33∙х3+ а34∙х4+ а35∙х5 ≤ В3

При этом нужно выполнять условие неотрицательности решения

х1≥0, х2≥0, х3≥0.

Шаг 4. Расчет прибыли от изготовления продукции.

Общая прибыль предприятия от изготовленной продукции имеет вид:

С=с1∙х1+с2∙х2+с3∙х3 +c4∙x4+c5∙x5+c6∙x6≥max- целевая функция.

Окончательная обобщенная математическая модель имеет вид:

Максимальная прибыль предприятия от изготовленной продукции Сmax=с1∙х1+с2∙х2+с3∙х3 +c4∙x4+c5∙x5+c6∙x6 будет обеспечена при условии:

а11∙х1+а12∙х2+а13∙х3+ а14∙х4+ а15∙х5 ≤ В1

а21∙х1+а22∙х2+а23∙х3+ а24∙х4+ а25∙х5 ≤ В2

а31∙х1+а32∙х2+а33∙х3+ а34∙х4+ а35∙х5 ≤ В3

х1≥0, х2≥0, х3≥0.

Выводы: Решение данной системы – это поиск неотрицательной комбинации ( х1,х2,х3 ) при ( xi≥0 ), ( оптимальный план ), при котором функция цели C = с1∙х1+с2∙х2+с3∙х3+c4∙x4+c5∙x5+c6∙x6 принимает наибольшее значение ( максимизируется ) .

3. Графическое решение задач линейного программирования.

Постановка задачи. Решить задачу линейного программирования. Определить значения х₁ и х₂, при которых функция цели С = ах + вх имеет экстремум, для ограничений типа

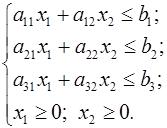
Во всех заданиях 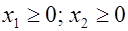. Варианты заданий представлены в табл. 3

Таблица 3

Вариант задания

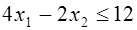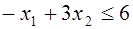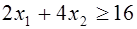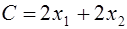Решение постановки задачи №3:

Решить задачу линейного программирования – это значит определить такие значения х₁, х₂, при которых целевая функция имеет экстремум в области, удовлетворяющей ограничениям:

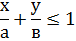
Решить графически систему (1) – это значит построить многоугольник, отражающий систему неравенств, и определить значение целевой функции в вершинах этого многоугольника. Экстремальному значению целевой функции и соответствует оптимальный план (х₁, х₂). Основная цель поиска оптимального плана состоит в нахождении функции цели (Ф) в вершинах многоугольника, полученного в результате решения заданной системы неравенств.

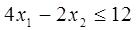Шаг 1: сформируем условие задачи:

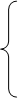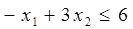
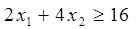
Х₁ 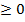Х₂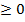

Функция цели имеет вид: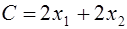

Шаг 2:Преобразуем систему неравенств к каноническому виду

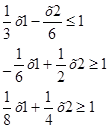
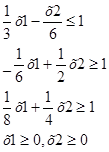
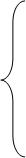
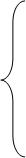Шаг 3 . Изобразим множество точек, удовлетворяющих условиям на плоскости ( рис. 1 ).

Прямая А Прямая Б Прямая В

графическое решение выше указанной системы неравенств представим в Табл. 3.2.

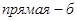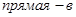x1	x2	x1	x2	x1	x2
		-6
	-6

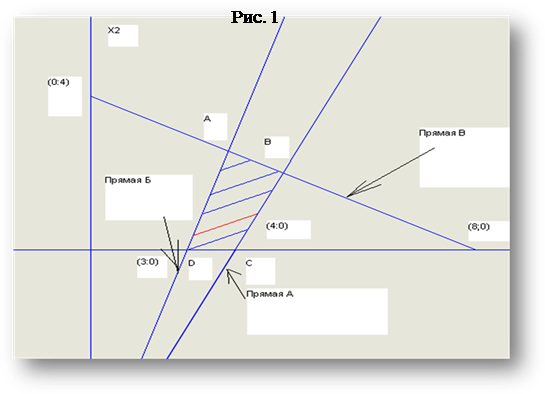Шаг 4: из полученной области АВСD определяем множество значений х₁, х₂, для которых выполняются соответствующие неравенства и координаты точек А, В, С и D.

Координаты точек имеют следующие значения: A(3.4;2.8) B(4.5;2) C(4;0) D(3;0)

Шаг 5: подставляя найденные координаты вершин многоугольника, находим значения целевой функции в этих вершинах: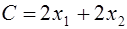

С(А)=12.4;

С(В)=13;

С(С)=8;

C(D)=6.

Вывод:

Min значение функция цели достигает в точке D(3;0)(х₁=3, х₂=0)

Max значение функция цели достигает в точке B(4.5;2) (х₁=4.5 х₂=2).