Задачи для самостоятельного решения. ПРОИЗВОДНАЯ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ

№	Задания	Ответы

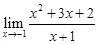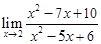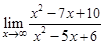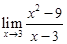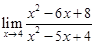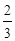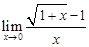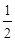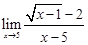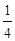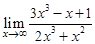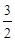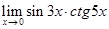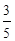Глава 2

ПРОИЗВОДНАЯ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ

Приращение аргумента и приращение функции

Пусть дана функция 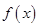. Зафиксируем некоторое значение 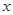. Дадим переменной 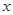произвольное приращение 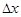. В точке 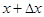функция будет иметь значение 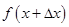. Разность между новым значением функции 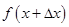и ее старым значением 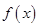называется приращением функции и обозначается 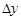. Таким образом, приращением функции называется величина

.

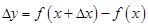Пример

Пусть 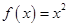, тогда 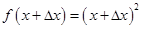. Найдем :

= .

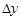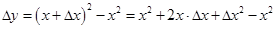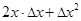2.2. Понятие производной.

Пусть 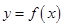— произвольная функция пере­менной х. Зафиксируем некоторое значение аргумента х и вычислим соответствующее значение функции 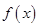. Придадим аргументу приращение 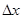, получим новое значе­ние 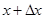и вычислим соответствующее приращение функции 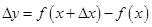. Составим отношение

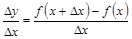
и рассмотрим предел

.

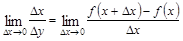Этот предел называется производной функции у = f(x) в точке х и обозначается у', у'_x , f'(x) или 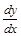. Таким образом, производной называется предел отношения прираще­ния функции к приращению аргумента, когда приращение аргу­мента стремится к нулю.

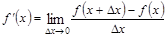
Операция нахождения производной функции на­зывается дифференцированием этой функции.

Геометрический смысл производной

Пусть функция у = f(x) имеет производную в точке x₀. Тогда к графику функции в точке М₀(x₀, y₀) можно провести касательную, уравнение которой имеет вид

,

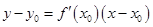В этом уравнении 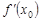= tga – где a – угол наклона касательной к оси Ох.

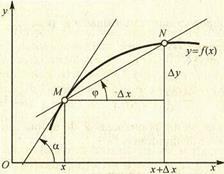
Рис.2.1

Таким образом, геометрически производная есть угловой коэффициент касатель­ной к кривой в рассматриваемой точке.

Физический смысл производной

Пусть точка движется по прямой так, что 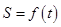– путь, пройденный точкой к моменту времени t. Тогда путь, пройденный точкой за промежуток времени Dt от момента t до момента t+Dt, равен DS = f(t+Dt)–f(t). В этом случае

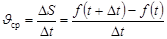
есть средняя скорость точки за промежуток времени от t до t+Dt.

Скоростью 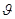точки в данный момент называется предел ее средней скорости за промежуток времени Dt, т.е.

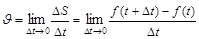
Из (1.2) и определения производной (1.1) следует, что 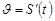, т.е. производная от пути по времени при прямолинейном движении есть скорость.

Правила вычисление производных

Справедливы следующие формулы, выражаю­щие правила дифференцирования суммы, произведения, частного функций, а также вычисления производной от постоянной величины .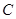

1) Производная постоянной величины 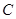равна нулю:

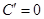
2) Производная суммы равна сумме производных:

.

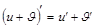Пример 2.1

.

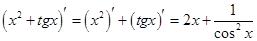3) Производная произведения:

.

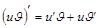Пример 2.2

.

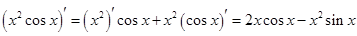4) Постоянную можно выносить за знак производной:

.

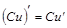Это правило является следствием правила 1) и правила 3).

Пример 2.3

.

5). Производная частного:

.

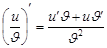Здесь предполагается, что рассматриваемые значения знаменателя не равны нулю.

Пример 2.4

=

= .
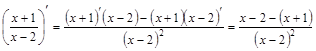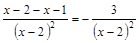