Свободный экстремум функции нескольких переменных
Рис. 2
через х и у – это координаты точки М (х,у) 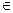 Х . График
Х . График
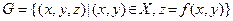 функции f (х,у) представлен на рис. 2б поверхностью, уравнение которой z = = f (x,y). При n = 3 область определения Х функции f можно изобразить на чертеже в виде некоторого геометрического тела . Аргументы функции обыч- но обозначают через х,у и z – это координаты точки, принадлежащей Х. График
функции f (х,у) представлен на рис. 2б поверхностью, уравнение которой z = = f (x,y). При n = 3 область определения Х функции f можно изобразить на чертеже в виде некоторого геометрического тела . Аргументы функции обыч- но обозначают через х,у и z – это координаты точки, принадлежащей Х. График 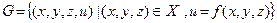 функции f (x,y,z) лежит в четы- рехмерном пространстве, и потому не может быть изображен на чертеже. Конечно, это относится и к графикам функций бóльшего, чем 3, количества переменных. Тем не менее при n ≥3 полезным бывает чертеж 2в) , на котором горизонтальная координатная плоскость условно представляет пространство
функции f (x,y,z) лежит в четы- рехмерном пространстве, и потому не может быть изображен на чертеже. Конечно, это относится и к графикам функций бóльшего, чем 3, количества переменных. Тем не менее при n ≥3 полезным бывает чертеж 2в) , на котором горизонтальная координатная плоскость условно представляет пространство 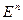 , множество определения Х функции f представлено фигурой, лежащей в этой плоскости, а график G функции f по аналогии со случаем n = 2 пред- ставлен этом чертеже поверхностью, уравнение которой xn+1= f(x1,x2,…,xn).
, множество определения Х функции f представлено фигурой, лежащей в этой плоскости, а график G функции f по аналогии со случаем n = 2 пред- ставлен этом чертеже поверхностью, уравнение которой xn+1= f(x1,x2,…,xn).
2.2. Предел функции
Пусть функция f определена на множестве 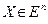 , а точка х0 является предельной точкой этого множества. Напомним, что х0 может принадлежать, но может и не принадлежать Х, так что f не обязательно определена в точке х0 . Пусть А – вещественное число.
, а точка х0 является предельной точкой этого множества. Напомним, что х0 может принадлежать, но может и не принадлежать Х, так что f не обязательно определена в точке х0 . Пусть А – вещественное число.
Определение 1. Вещественное число называют пределом функции f при х, стремящемся к х0 по множеству Х, если для любой последовательно- сти {xk} элементов множества Х , все члены которой отличны от х0 , и кото- рая сходится к х0 , соответствующая последовательность {f (xk)} значений функции сходится к А.
Если А является пределом функции f при х, стремящемся к х0 по мно- жеству Х,будем записывать А = 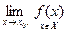 или f (x)
или f (x) 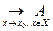 . Таким образом, ра- венство А=
. Таким образом, ра- венство А= 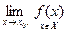 означает:
означает: 
 {xk}
{xk} 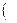 (
( 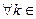 N xk
N xk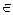 X, xk
X, xk 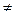 х0)
х0) 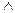 ( xk→ x0)
( xk→ x0) 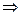 f (xk)→ A
f (xk)→ A 
Пример 1. Пусть 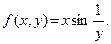 Этим равенством f определена на всей плоскости ХОY , за исключением точек оси абсцисс, так что здесь Х= ={Р(x,y)| y≠ 0). Очевидно, что всякая точка оси абсцисс является предель- ной точкой для множества Х. Покажем, что 1) А=0 является пределом функ- ции f, когда точка Р(х,у) стремится к началу координат О(0,0) по множеству Х и 2) функция f не имеет предела, когда точка Р(х,у) стремится по множе- ству Х к любой точке на оси абсцисс, отличной от начала координат О .
Этим равенством f определена на всей плоскости ХОY , за исключением точек оси абсцисс, так что здесь Х= ={Р(x,y)| y≠ 0). Очевидно, что всякая точка оси абсцисс является предель- ной точкой для множества Х. Покажем, что 1) А=0 является пределом функ- ции f, когда точка Р(х,у) стремится к началу координат О(0,0) по множеству Х и 2) функция f не имеет предела, когда точка Р(х,у) стремится по множе- ству Х к любой точке на оси абсцисс, отличной от начала координат О .
1) Пусть {Рk 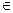 (xk,yk)} , где
(xk,yk)} , где 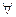 k
k 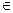 Nyk ≠ 0, - последовательность точек, сходящаяся к началу координат О. Заметим:
Nyk ≠ 0, - последовательность точек, сходящаяся к началу координат О. Заметим: 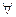 k
k 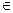 N (Рk
N (Рk 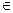 X)
X) 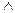 (Рk→O). В силу теоремы о покоординатной сходимости хk→ 0 и yk→ 0. Имеем:
(Рk→O). В силу теоремы о покоординатной сходимости хk→ 0 и yk→ 0. Имеем: 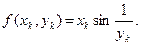 . Последовательность { хk} – бесконечно малая, а последо- вательность {
. Последовательность { хk} – бесконечно малая, а последо- вательность { 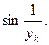 }, очевидно, ограничена; по теореме о произведении бес- конечно малой последовательности на ограниченную ([2], п.3.4) получаем :
}, очевидно, ограничена; по теореме о произведении бес- конечно малой последовательности на ограниченную ([2], п.3.4) получаем :  . Так как {Рk
. Так как {Рk  (xk,yk)} – произвольная последовательность, удов- летворяющая требованиям
(xk,yk)} – произвольная последовательность, удов- летворяющая требованиям  k
k 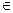 N Рk
N Рk 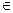 Х и Рk→ О, указанным в определении 1, то утверждение 1) доказано.
Х и Рk→ О, указанным в определении 1, то утверждение 1) доказано.
2) Пусть Р0 – некоторая точка оси абсцисс, отличная от начала коорди- нат, т.е., Р0(х0 ,0), где х0 ≠ 0. Рассмотрим последовательности { 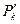 (xk,
(xk, 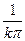 )} и {
)} и { 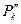 (xk,
(xk, 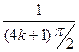 )}, где { хk} – некоторая числовая последовательность, сходящаяся к х0 . Очевидно, каждая из последовательностей {
)}, где { хk} – некоторая числовая последовательность, сходящаяся к х0 . Очевидно, каждая из последовательностей { 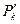 k } и {
k } и { 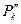 } сходится к Р0 и удовлетворяет требованиям, указанным в определении 1, при чем соответствующие им последовательности значений функции имеют раз- личные пределы: f(
} сходится к Р0 и удовлетворяет требованиям, указанным в определении 1, при чем соответствующие им последовательности значений функции имеют раз- личные пределы: f( 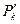 ) = хk sin kπ → 0 ; f(
) = хk sin kπ → 0 ; f( 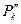 ) = хk sin(4k+1)
) = хk sin(4k+1) 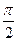 → х0 ≠ 0. Этого достаточно для вывода: число А, удовлетворяющее определению 1, не существует.
→ х0 ≠ 0. Этого достаточно для вывода: число А, удовлетворяющее определению 1, не существует.
Определение 1 высказано на языке последовательностей. Сформулируем эквивалентное определение на языке ″ε–δ″.
Пусть функция f определена на множестве 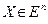 , а точка х0 является пре дельной точкой этого множества.
, а точка х0 является пре дельной точкой этого множества.
Определение2. Вещественное число А называют пределом функции f при х, стремящемся к х0 по множеству Х, если для любого положительного ε существует δ > 0 такое, что для всякого х, принадлежащего Х и удовлетворя- ющего условиям 0<ρ(х, х0) < δ, справедливо неравенство | f(х) – A | < ε .
Таким образом, равенство А= 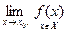 , где А – число, означает:
, где А – число, означает:
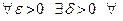 х
х 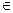
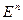 ( 0< ρ(х, х0) < δ
( 0< ρ(х, х0) < δ 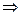 | f(х) – A | < ε )
| f(х) – A | < ε )
Определения 1 и 2 аналогичны определениям предела функции одной переменной; доказательство эквивалентности определений 1 и 2 проводится аналогично одномерному случаю ([1], п. 20.2). Аналогичны одномерному случаю формулировки и доказательства теорем об основных свойствах пре- делов: о единственности предела, о стабилизации знака неравенства, о пре -дельном переходе в неравенстве, о ″сжатой″ функции, об арифметических действиях с пределами, о разности между функцией и числом ([2],п.п. 4.5, 4.6). В качестве примера приведем формулировку и доказательство теоремы о стабилизации знака неравенства.
Теорема. Пусть А= 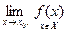 и пусть р > A (p < A). Тогда существует положительное δр такое, что при всяком х, принадлежащем Х и удовлетво- ряющем условию 0< ρ(х, х0) < δр, справедливо неравенство р > f(х) (f(х) < <p).
и пусть р > A (p < A). Тогда существует положительное δр такое, что при всяком х, принадлежащем Х и удовлетво- ряющем условию 0< ρ(х, х0) < δр, справедливо неравенство р > f(х) (f(х) < <p).
► Доказательство проведем для случая р > A. Обозначим: ε = р-А . В силу определения 2 существует δ > 0 такое,что при всяком х , которое при – надлежит Х и удовлетворяет неравенствам 0< ρ(х, х0) < δ справедливо | f(х)- – A | < ε , т.е. – ε < f(х)- А < ε . Отсюда для указанных х получаем: f(х) < ε +А = р . Таким образом, δр существует: можно положить δр = δ .◄
В определении 2 А – вещественное число. Для А , равного +∞, - ∞ или ∞ , в определении 2 нужно лишь заменить неравенство | f(х) – A | < ε на f(х) > >ε , f(х) < - ε или | f(х)| > ε соответственно. Функции, удовлетворяющие та- ким условиям называют бесконечно большими при х, стремящемся к х0 по множеству Х.
Рассматриваемые ниже функции чаще всего определены в окрестности или в проколотой окрестности точки х0 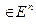 . Окрестностью точки х0 мы на- зываем любое открытое множество, содержащее х0. Обозначать такое множе- ство будем символом
. Окрестностью точки х0 мы на- зываем любое открытое множество, содержащее х0. Обозначать такое множе- ство будем символом 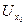 . Проколотой окрестностью точки х0 назовем вся -кую ее окрестность, из которой удалена сама точка х0; обозначать это множе- ство будем символом
. Проколотой окрестностью точки х0 назовем вся -кую ее окрестность, из которой удалена сама точка х0; обозначать это множе- ство будем символом 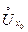 :
: 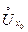 = { х
= { х 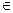
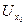 | х
| х 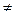 х0} . Заметим, что функция, определенная в окрестности
х0} . Заметим, что функция, определенная в окрестности 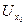 , определена в точке х0 ; если же функция определена в проколотой окрестности
, определена в точке х0 ; если же функция определена в проколотой окрестности 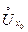 ,то в точке х0 она может быть определена, но может быть и нет.
,то в точке х0 она может быть определена, но может быть и нет.
Точка х0 = 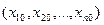 является предельной для множеств
является предельной для множеств 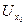 и
и 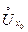 . Если функция f определена на одном из этих множеств, то ее предел при х, стремящемся к х0 по
. Если функция f определена на одном из этих множеств, то ее предел при х, стремящемся к х0 по 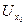 или по
или по 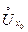 называют пределом функции f в точке х0 и обозначают через
называют пределом функции f в точке х0 и обозначают через 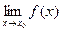 или через
или через 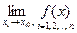 .
.
2.3. Непрерывность функции в точке
Пусть функция f определена на множестве 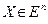 , а х0 принадлежит Х иявляется предельной точкой этого множества.
, а х0 принадлежит Х иявляется предельной точкой этого множества.
Определение1. Будем говорить, что функция f непрерывна в точке х0 по множеству Х, если 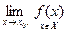 = f(х0) , т.е. если (на языке последовательностей)
= f(х0) , т.е. если (на языке последовательностей)
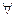 {xk}
{xk} 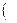 (
( 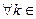 N xk
N xk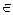 X)
X)  ( xk→ x0)
( xk→ x0)  f (xk)→ f(х0)
f (xk)→ f(х0) 
или (на языке ″ε–δ″)
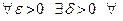 х
х 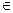
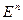 ( ρ(х, х0) < δ
( ρ(х, х0) < δ 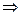 | f(х) – f(х0) | < ε )
| f(х) – f(х0) | < ε )
Замечание. В отличие от определений 1 и 2 предыдущего пункта, в при- веденной выше записи на языке последовательностей отсутствует трeбование xk ≠ x0 , а в записи на языке ″ε–δ″ снято требование ρ(х, х0) > 0. Тем самым членам последовательности {xk} и точке х разрешено принимать значение x0 . Снятые требования здесь излишни, поскольку функция определена в x0 , а ее значение f(х0) является и ее пределом.
Определение2. Будем говорить, что функция f непрерывна в точке х0 , если она определена в некоторой окрестности 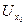 и если
и если 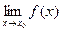 = f(х0).
= f(х0).
Пример 1. 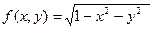 . Этим равенством функция определена в замкнутом единичном круге Х =
. Этим равенством функция определена в замкнутом единичном круге Х =  . Она непрерывна в каж -дой внутренней точке этого круга. Действительно, пусть Р0(х0,у0) – внутрен- няя точка,т.е.
. Она непрерывна в каж -дой внутренней точке этого круга. Действительно, пусть Р0(х0,у0) – внутрен- няя точка,т.е. 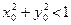 . Найдется d > 0 такое, что d – окрестность
. Найдется d > 0 такое, что d – окрестность  со- держится в Х ( d < 1-
со- держится в Х ( d < 1- 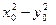 ) . Пусть последовательность {Рk(xk,yk)} тако- ва, что 1)
) . Пусть последовательность {Рk(xk,yk)} тако- ва, что 1) 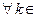 NРk
NРk 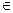
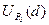 и 2) Рk → Р0. Тогда xk → x0 и yk → y0 ; поэтому
и 2) Рk → Р0. Тогда xk → x0 и yk → y0 ; поэтому
 f (Рk) =
f (Рk) =  .
.
Так как {Рk(xk,yk)} – произвольная последовательность, удовлетворяю- щая требованиям 1) и2), то доказано равенство 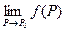 = f(Р0), т.е. доказана непрерывность f в любой внутренней точке круга Х. Что касается его гра- ничных точек, т.е. точек единичной окружности, то в каждой из них функция непрерывна по множеству Х. Доказательство этого аналогично приведенному выше.
= f(Р0), т.е. доказана непрерывность f в любой внутренней точке круга Х. Что касается его гра- ничных точек, т.е. точек единичной окружности, то в каждой из них функция непрерывна по множеству Х. Доказательство этого аналогично приведенному выше.
Пусть функция f определена на некотором множестве Х 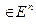 , а точка х0 принадлежит Х. Пусть h = (h1,h2, …,hn) – вектор такой, что х0+ h
, а точка х0 принадлежит Х. Пусть h = (h1,h2, …,hn) – вектор такой, что х0+ h 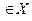 . Раз- ность f (х0+ h) - f(х0) = f (х10+ h1, x20 +h2,…,xn0+hn) - f(х10, x20 ,…,xn0) назовем приращением функции f в точке х0. Обозначать эту величину будем символами Δ f и Δ
. Раз- ность f (х0+ h) - f(х0) = f (х10+ h1, x20 +h2,…,xn0+hn) - f(х10, x20 ,…,xn0) назовем приращением функции f в точке х0. Обозначать эту величину будем символами Δ f и Δ 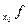 ( h); второй из них будем употреблять тогда, когда желательно подчеркнуть, что приращение функции само является функцией n переменных h1,h2, …,hn. Eсли f определена в некоторой окрестности
( h); второй из них будем употреблять тогда, когда желательно подчеркнуть, что приращение функции само является функцией n переменных h1,h2, …,hn. Eсли f определена в некоторой окрестности 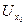 , то ее приращение Δ
, то ее приращение Δ 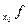 ( h) есть функция, определенная в некоторой окрест- ности точки 0=(0,0, ....,0), причём Δ
( h) есть функция, определенная в некоторой окрест- ности точки 0=(0,0, ....,0), причём Δ 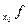 ( 0) = 0.
( 0) = 0.
Теорема1. (О приращении непрерывной функции) Пусть функция 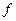 определена в окрестности
определена в окрестности 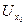 точки х0 ,х0
точки х0 ,х0 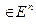 . Для того, чтобы функция
. Для того, чтобы функция 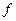 была непрерывной в точке х0, необходимо и достаточно, чтобы ее прираще- ние Δ
была непрерывной в точке х0, необходимо и достаточно, чтобы ее прираще- ние Δ 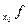 ( h) стремилось к нулю при h→ 0.
( h) стремилось к нулю при h→ 0.
► Δ 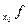 ( h) = f (х0+ h) - f(х0) = f (х) - f(х0) , где х =х0+ h . Заметим: (х→ х0)
( h) = f (х0+ h) - f(х0) = f (х) - f(х0) , где х =х0+ h . Заметим: (х→ х0) 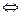 (h→ 0). По теореме о разности между функцией и числом (f (х)
(h→ 0). По теореме о разности между функцией и числом (f (х) 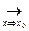 f(х0))
f(х0)) 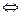 (f (х) - f(х0)
(f (х) - f(х0) 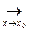 0). Таким образом, f непрерывна в х0 ( т.е.f (х)
0). Таким образом, f непрерывна в х0 ( т.е.f (х) 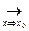 f(х0)) тогда и только тогда, когда Δ
f(х0)) тогда и только тогда, когда Δ 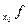 ( h)
( h) 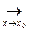 0, а это равносильно Δ
0, а это равносильно Δ 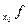 ( h)
( h) 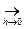 0. ◄
0. ◄
Приведенная теорема и ее доказательство аналогичны формулировке и доказательству теоремы о приращении непрерывной функции одной пере - менной. Это же можно сказать и о следующих двух теоремах.
Теорема 2.( О стабилизации знака непрерывной функции). Пусть функ- ция f непрерывна в точке х0 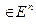 . Если f(х0) ≠ 0, то существует δ > 0 такое, что при всяком х
. Если f(х0) ≠ 0, то существует δ > 0 такое, что при всяком х 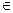
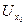 ( δ) справедливо f (х) · f(х0) > 0.
( δ) справедливо f (х) · f(х0) > 0.
Теорема 3.(Об арифметических действиях с непрерывными функциями)
Пусть функции f и g непрерывны в точке х0 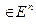 . Тогда их сумма f + g и произведение f · g непрерывны в х0 . Если g(х0) ≠ 0, то и их частное
. Тогда их сумма f + g и произведение f · g непрерывны в х0 . Если g(х0) ≠ 0, то и их частное 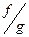 есть непрерывная в точке х0 функция.
есть непрерывная в точке х0 функция.
Пусть n функций φ1(t), φ2(t), …, φn(t) определены на множестве Т 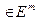 (n и m – некоторые натуральные числа). Обозначим: хt = (φ1(t), φ2(t), …, φn(t)), X = { хt| t
(n и m – некоторые натуральные числа). Обозначим: хt = (φ1(t), φ2(t), …, φn(t)), X = { хt| t  T }. Ясно, что Х
T }. Ясно, что Х 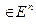 . Пусть на Х определена функция f. Зададим на множестве Т функцию F :
. Пусть на Х определена функция f. Зададим на множестве Т функцию F : 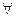 t
t  T F(t) = f(хt) = f(φ1(t), φ2(t), …, φn(t) ). Функцию F называют композицией или суперпозицией функций f и φ1,φ2,…, φn; F называют также сложной функцией.
T F(t) = f(хt) = f(φ1(t), φ2(t), …, φn(t) ). Функцию F называют композицией или суперпозицией функций f и φ1,φ2,…, φn; F называют также сложной функцией.
Теорема 4. ( О непрерывности сложной функции)Пусть функции φ1(t), φ2(t), …, φn(t) непрерывны в точке t0 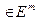 , а функция f непрерывна в точке x0 =(x10,x20, …,xn0), где xi0 = φi(t0), i = 1,2,…,n. Тогда сложная функция F(t) = = f(φ1(t), φ2(t), …, φn(t) ) непрерывна в точке t0 .
, а функция f непрерывна в точке x0 =(x10,x20, …,xn0), где xi0 = φi(t0), i = 1,2,…,n. Тогда сложная функция F(t) = = f(φ1(t), φ2(t), …, φn(t) ) непрерывна в точке t0 .
► Нужно доказать два утверждения: 1) функция F определена в неко- торой окрестности точки t0 и 2) 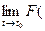 t) =F(t0).
t) =F(t0).
1) По условию f непрерывна в точке x0 . Это означает, в частности, что она определена в некоторой окрестности этой точки; поэтому можно подобрать ε >0 так, чтобы f была определена в 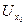 ( ε ). При каждом i = 1,2,…,n функция φ i непрерывна в t0 , значит, для каждого i найдется δ i > 0 такое, что
( ε ). При каждом i = 1,2,…,n функция φ i непрерывна в t0 , значит, для каждого i найдется δ i > 0 такое, что 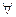 t
t 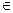
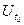 ( δ i ) выполняется | φ i (t )- x i 0| <
( δ i ) выполняется | φ i (t )- x i 0| < 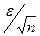 . Обозначим через δ наи- меньшее из δ1, δ2,…., δn. Если t
. Обозначим через δ наи- меньшее из δ1, δ2,…., δn. Если t 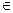
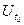 ( δ) ,то справедливо каждое из неравенств | φ i (t )- x i 0| <
( δ) ,то справедливо каждое из неравенств | φ i (t )- x i 0| < 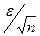 , i = 1,2,…,n; поэтому || хt - x0|| =
, i = 1,2,…,n; поэтому || хt - x0|| = 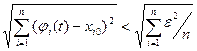 = =ε. Таким образом, при всех t
= =ε. Таким образом, при всех t 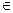
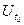 ( δ) точка хt содержится в
( δ) точка хt содержится в 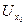 ( ε ); поэтому F(t) = f(хt) определена в
( ε ); поэтому F(t) = f(хt) определена в 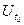 ( δ).
( δ).
2) Пусть {tk} – некоторая последовательность такая, что а) 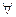 k
k 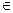 Ntk
Ntk 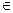
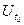 ( δ) и б) tk → t0. Обозначим: xk = ( φ1(tk), φ2 (tk),…, φn(tk)). Функции φi непрерывны в точке t0, поэтому φi(tk) → φi(t0) = xi0 , i = 1,2,…,n. Значит, xk→ х0 и так как f непрерывна в точке х0 , то f(xk) →f (x0). Рассмотирим последо- вательность F(tk ). Имеем:
( δ) и б) tk → t0. Обозначим: xk = ( φ1(tk), φ2 (tk),…, φn(tk)). Функции φi непрерывны в точке t0, поэтому φi(tk) → φi(t0) = xi0 , i = 1,2,…,n. Значит, xk→ х0 и так как f непрерывна в точке х0 , то f(xk) →f (x0). Рассмотирим последо- вательность F(tk ). Имеем:
F(tk ) = f(φ1(t k), φ2(t k), …, φn(t k)) = f(xk) →f (x0) = F(t0 ).
Так как {tk} - произвольная последовательность, удовлетворяющая условиям а) и б), то равенство 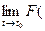 t) =F(t0) доказано. ◄
t) =F(t0) доказано. ◄
2.4. Непрерывность функции на множестве
Определение 1. Будем говорить, что функция f непрерывна на множе- стве Х , если она определена на этом множестве и непрерывна по множеству Х в каждой предельной точке, принадлежащей Х.
Пример. Функция 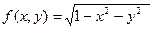 непрерывна на замкнутом множе- стве Х =
непрерывна на замкнутом множе- стве Х = 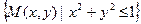 - этот факт был установлен в примере 1, п. 2.3.
- этот факт был установлен в примере 1, п. 2.3.
Справедливы теоремы, аналогичные теоремам Вейерштрасса о функци- ях одной переменной ( [2],п. 5.3).
Теорема 1. (Первая теорема Вейерштрасса ) Если функция f непре –рывна на замкнутом ограниченном множестве Х 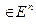 , то она ограничена на этом множестве, т.е. существуют числа А и В , А < В, такие, что при всех х
, то она ограничена на этом множестве, т.е. существуют числа А и В , А < В, такие, что при всех х  Х А ≤ f(х) ≤ В.
Х А ≤ f(х) ≤ В.
Теорема 2 ( Вторая теорема Вейерштрасса ) Функция f, непрерывная на замкнутом ограниченном множестве Х 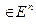 , достигает на этом множестве своих точных граней, т.е. в Х существуют точки х
, достигает на этом множестве своих точных граней, т.е. в Х существуют точки х 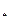 и х
и х 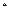 такие, что f(х
такие, что f(х 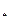 ) и f(х
) и f(х 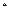 ) являются соответственно точной нижней и точной верхней гранями функции f на множестве Х.
) являются соответственно точной нижней и точной верхней гранями функции f на множестве Х.
Доказательства этих теорем можно найти в [1].
Теорема 3. ( Теорема Коши о промежуточном значении) Пусть функ- ция f непрерывна в области Х 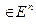 , х1 и х2 – две точки, принадлежащие Х , А = f(х1), В = f(х2). Если А ≠ В, то для любого числа С , заключенного между А и В в области Х существует точка ξС такая, что f(ξС) = С.
, х1 и х2 – две точки, принадлежащие Х , А = f(х1), В = f(х2). Если А ≠ В, то для любого числа С , заключенного между А и В в области Х существует точка ξС такая, что f(ξС) = С.
► Пусть γ – непрерывнвя кривая, содержащаяся в Х и соединяющая х1 и х2 ( так как Х – область, такая γ существует, см. определение 1, п. 1.4), а
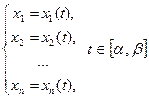
- параметрические уравнения этой кривой, причем х1 =( х1(α), х2(α ),…, хn(α )) , х2 = ( х1(β), х2(β ),…, хn(β )). На [α , β] зададим функцию F (t) = f( х1(t), х2(t ), …, хn(t )). Эта функция непрерывна на [α , β], так как является суперпозицией непрерывных функций, причем F (α) = f (х1) =А, F (β) = f (х2) =В. Пусть С заключено между А и В. По теореме Коши о промежуточном значении функции одной переменной ( [2],п. 5.3) на (α , β ) найдется τ такое, что F (τ ) = С. Положим ξС = ( х1(τ), х2(τ),…, хn(τ)) . Тогда f(ξС) = F(τ) = С. ◄
Определение 2. Будем говорить, что функция f равномерно непрерывна на множестве Х 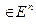 , если для любого ε > 0 существует δ > 0 такое, что для любых двух элементов х′ и х″ множества Х, удовлетворяющих условию || х′ - х″|| < δ, справедливо неравенство | f (х′) - f (х″) | < ε :
, если для любого ε > 0 существует δ > 0 такое, что для любых двух элементов х′ и х″ множества Х, удовлетворяющих условию || х′ - х″|| < δ, справедливо неравенство | f (х′) - f (х″) | < ε :
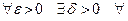 х′
х′ 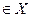
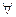 х″
х″ 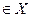 (|| х′ - х″|| < δ
(|| х′ - х″|| < δ 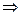 | f (х′) - f (х″) | < ε).
| f (х′) - f (х″) | < ε).
Нетрудно показать, что если функция равномерно непрерывна на множестве, то она и непрерывна на нем. Обратное утверждение, вообще говоря, неверно: из непрерывности функции на множестве не вытекает ее равномерная непрерывность. Вместе с тем, справедлива теорема Кантора :если функция непрерывна на замкнутом ограниченном множестве, то она и равномерно непрерывна на нем. Доказательство см. [1].
§ 3. Частные производные и дифференциал функции n, n 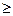 2,
2,
Переменных
3.1 Частные производные функции двух переменных в точке
Пусть функция f определена в окрестности U 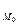 точки М0 (х0,у0). Положим φ(х) = f( х,у0). Этим равенством функция φ определена для тех х, для которых точка М(х,у0) принадлежит U
точки М0 (х0,у0). Положим φ(х) = f( х,у0). Этим равенством функция φ определена для тех х, для которых точка М(х,у0) принадлежит U 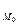 , т.е. φ определена в некоторой окрестности U
, т.е. φ определена в некоторой окрестности U  =( a,b ), где a<x0<b.
=( a,b ), где a<x0<b.
Определение 1. Если существует производная φ′(х0), то это число называют частной производной функции f по аргументу х в точке М0 .
Обозначают введенную этим определением частную производную символами fх′(M0) или fх′(x0,y0) , а также 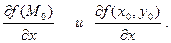
Таким образом,
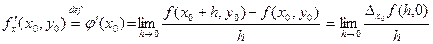
Пример 1. 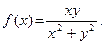 Функция f определена этим равенством во всех точках плоскости
Функция f определена этим равенством во всех точках плоскости 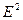 , за исключением начала координат О(0,0). Пусть М0 (х0 ,у0) – некоторая точка, отличная от О. Найдем fх ′(M0). Имеем:
, за исключением начала координат О(0,0). Пусть М0 (х0 ,у0) – некоторая точка, отличная от О. Найдем fх ′(M0). Имеем: 
Из свойств производной φ′ вытекают свойства частной производной  : пусть функции f и g определены в окрестности точки М0 и пусть существу- ют производные
: пусть функции f и g определены в окрестности точки М0 и пусть существу- ют производные  (M0) и
(M0) и 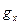 (M0) ; тогда
(M0) ; тогда
1) существует hх′(M0), где h= f + g, причем hх′(M0) = fх′(M0) + gх′(M0) ;
2) существует hх′(M0), где h= f g, причем
hх′(M0) = fх′(M0) g(M0) + f(M0) gх′(M0) ;
3) если g(M0) ≠ 0, то существует hх′(M0), где h= 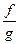 , причем
, причем
hх′(M0) = 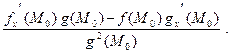
|







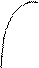




G

 Выясним геометрический смысл числа
Выясним геометрический смысл числа
 fх′(M0). Пусть G есть график функции f,
fх′(M0). Пусть G есть график функции f,
т.е. поверхность с уравнением z =f(x,y).
Обозначим через Г линию пересечения

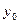 G с плоскостью у = у0. Уравнение Г
G с плоскостью у = у0. Уравнение Г
запишем в виде системы 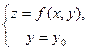 .
.
 Исключив из этой системы у,
Исключив из этой системы у,
получим уравнение линии γ -
проекции Г на плоскость ХОZ : z = f(x,y0) = φ(x)
(рис.3). Производная φ′(х0) есть тангенс угла наклона к оси абсцисс касатель- ной l к кривой γ в точке Р0 , абсцисса которой равна х0 . Заметим, что кривые γ и Г конгруентны (получаются одна из другой параллельным переносом), а Р0 есть проекция точки N0(x0,y0,z0), где z0=f(x0,y0) . Значит, касательная L к кривой Г в точке N0 параллельна касательной l кγ в точке Р0. Отсюда заключаем: пусть Г есть линия пересечения графика функции с плоскостью, проходящей через точку М0 перпендикулярно к оси ординат, а N0 - точка на Г, проекция которой на ХОУ есть М0; частная производная fх′(M0) равна тангенсу угла между осью абсцисс и касательной к Г, проведенной в точкеN0.
Аналогично определяется fу′(M0) – частная производная функции f по аргументу у в точке М0(х0,у0): fу′(M0)  ψ′(у0) , где ψ(у) = f(x0,y).
ψ′(у0) , где ψ(у) = f(x0,y).
Пример 2. 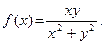 . Найдем fу′(M0), где М0(х0,у0) – некоторая точка плоскости, отличная от О(0,0). Имеем: ψ(у) = f(x0,y)=
. Найдем fу′(M0), где М0(х0,у0) – некоторая точка плоскости, отличная от О(0,0). Имеем: ψ(у) = f(x0,y)= 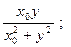
fу′(M0)  ψ′(у0) =
ψ′(у0) = 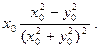
Очевидно, частная производная функции f по у обладает свойствами, аналогичными свойствам 1),2) и 3) частной производной по х. Геометрии- ческий смысл числа fу′(M0) выясняется так же, как это было сделано выше для fх′(M0): пусть Г есть линия пересечения графика G : z =f(x,y) c плоско- стью х =х0 ; fу′(х0,у0) есть тангенс угла между осью ординат и касательной к Г , проведенной в точке N0(x0,y0,z0), где z0=f(x0,y0).
3.2 Частные производные функции n переменных
Пусть функция f(х), х =(х1,х2,…,хn) определена в окрестности U  точки х0 = (
точки х0 = ( 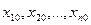 ). Выбрав одно из чисел 1,2,…,n ,обозначим его через i и положим φi(t) = f (xt) , где xt =
). Выбрав одно из чисел 1,2,…,n ,обозначим его через i и положим φi(t) = f (xt) , где xt = 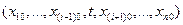 - точка, координаты которой совпадают с координатами х0, за исключением i-той координаты, равной t. Так как f определена в окрестности точки х0, функция φi определена для t, близких к числу xi0 , т.е. в окрестности Ux
- точка, координаты которой совпадают с координатами х0, за исключением i-той координаты, равной t. Так как f определена в окрестности точки х0, функция φi определена для t, близких к числу xi0 , т.е. в окрестности Ux 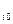 .
.
Определение 2. Если существует производная φ′i(xi0) , то это число называют частной производной от функции f по аргументу xi в точке х0 .
Обозначают частную производную, введенную определением 2 символами f ′х 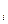 ( х0)и
( х0)и 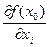 . Таким образом,
. Таким образом,
f ′х 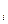 ( х0)
( х0)  φ′i(xi0)=
φ′i(xi0)= 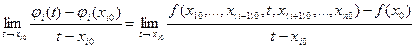 .
.
Обозначим : h= t - xi0. Тогда t = xi0+ h ; h →0 при t → xi0. Значит,
f ′х 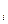 ( х0) =
( х0) = 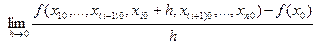 =
= 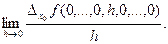
Свойства f ′х 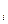 ( х0) вытекают из свойств производной φ′i(xi0) – они аналогичны утверждениям 1), 2) и 3) ,п.3.1.
( х0) вытекают из свойств производной φ′i(xi0) – они аналогичны утверждениям 1), 2) и 3) ,п.3.1.
