Интуитивное определение алгоритма

Основным понятием теория алгоритмов является понятие алгоритма.

Алгоритмом называется точное предписание, определяющее вычислительный процесс, который ведет от варьируемых исходных данных к искомому результату, т.е. алгоритм – это совокупность правил, определяющих данный вычислительный процесс (процедура).

Данная процедура предполагает наличие некоторых начальных или исходных данных Р (входной объект) и направлена на получение обусловленного этими данными определенного результата Q (объекта на выходе). Например, при вычислении ранга матрицы начальными данными служит прямоугольная таблица, составленная из n´m рациональных чисел, а результат — натуральное число, являющееся рангом данной матрицы.

Вычислительная процедура состоит из отдельных, элементарных шагов – тактов работы алгоритма. Каждый шаг заключается в смене одного набора данных другим набором. Переход от предыдущего состояния к последующему происходит по заранее заданному конечному набору инструкций.

Пусть некоторый алгоритм имеет исходный набор данных Р. Возможны три случая протекания алгоритмического процесса.

1. На некотором шаге возникает состояние, опознаваемое как заключительное. При этом происходит остановка вычислений и выдается результат Q.

2. Каждое очередное состояние сменяется последующим до бесконечности, т.е. процесс вычислений никогда не останавливается.

3. При некотором состоянии возникает ситуация, когда процесс вычислений обрывается без выдачи результата (например, не срабатывает инструкция для определения результата вычислений). Тем самым нет перехода к следующему шагу и нет результата вычислений. В этом случае говорят, что произошла безрезультативная остановка.

Считается, что алгоритм применим к исходному набору данных Р тогда и только тогда, когда выполнен первый случай. При этом алгоритм должен обладать определенными свойствами (см. [1, часть 8, п. 2], [2, §14.1].

Далее рассмотрим еще два варианта определения алгоритма – рекурсивные функции и машину Тьюринга.

Рекурсивные функции

Рассмотрим класс арифметических функций 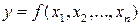, определенных на множестве 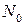. Под множеством 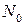будем понимать множество натуральный чисел 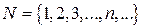и ноль, т.е. .

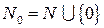Если это необходимо, в обозначении такой функции используется верхний индекс n, который указывает на число независимых переменных. Так, функция 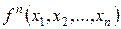зависит от 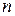переменных и называется n-арной. Таким образом, 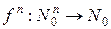. При этом эти функции могут быть частично определенными, т.е. определенные не для всех наборов натуральных чисел. Множество всех наборов значений, для которых функция определена, называется областью определения функции. Множество всех значений функции называется областью значений функции.

Функция называется всюду определенной, если она определена для любого набора .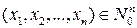

Арифметические функции вида 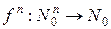, для которых существует алгоритм их вычисления, называются вычислимыми функциями.

Под рекурсией или рекурсивной функцией понимается метод определения функции через её предыдущие и ранее определенные значения, а также способ организации вычислений, при котором функция вызывает сама себя с другим аргументом.

Рекурсивные функции являются частично определенными функциями, поэтому их часто называют частично рекурсивными функциями. Рекурсивные функции, определённые при любых значениях аргументов, называют общерекурсивными функциями.

Классический пример функции, определение которой может задаваться в рекурсивной форме – определение «факториала» :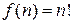

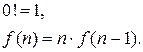
Прежде чем строить рекурсивные функции, полезно вспомнить, как определяются элементарные функции. Вначале рассматривается несколько классов функций: алгебраические, тригонометрические, показательные, логарифмические. Элементарная функция определяется как суперпозиция этих функций (сложная функция).

Рекурсивные функции строятся аналогичным образом.

Рассмотрим вначале некоторый набор простейших функций, вычислимость которых очевидна. Такие функции называются примитивно-рекурсивными функциями.

Простейшие примитивно-рекурсивные функциизадаются следующим образом.

1. Функция следования. Рассмотрим функцию, которая задается формулой:

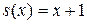(или ).

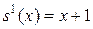Эта функция очевидно является вычислимой, т.к. алгоритм ее вычисления состоит из простейшего действия «добавления к х единичкам еще одной единицы».

2. Функция аннулирования. Пусть 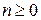. Рассмотрим n-арную функцию 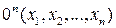, заданную правилом:

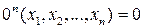для всех .

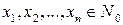Эта функция называется нулевой функцией. Очевидно. что она вычислима. Нулевую функцию при 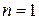обозначают через 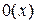. Поэтому

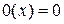для всех .

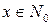Нулевая функция при 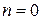обозначается через 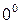и отождествляется с числом 0.

3. Функция тождества. Функция тождества или проектирования определяется следующим образом:

,

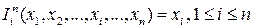то есть эта функция произвольному n-мерному вектору сопоставляет его 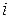-ю координату. Вычислимость функции тождества обеспечивается нашей способностью найти в строке 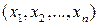место с номером i и указать число на этом месте.

Имея набор простейших (базисных) примитивно-рекурсивных функций, можно получить новые вычислимые примитивно-рекурсивные и частично рекурсивные функции с помощью следующих трех операторов.

1. Оператор суперпозиции. Пусть задана функция 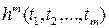от т переменных и заданы m функций 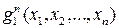, , 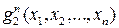…, 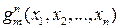от n переменных, Тогда новую функцию 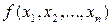определим по правилу:

.

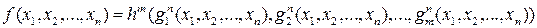Функция f является частично определенной функцией от n переменных. Ее значение 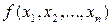определено тогда и только тогда, когда определены все выражения в правой части последнего соотношения. Если функции h, g₁, g₂, …, g_m вычислимы, то и функция f также вычислима.

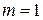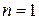В частности, при и функция 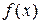получается с помощью оператора суперпозиции из функци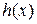й и 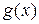следующим образом:

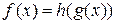для всех .

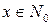Пример 12. Функцию 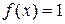получить суперпозицией функций 0(x) и s(x).

Р е ш е н и е. По условию 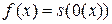. Поэтому

.►

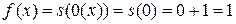Аналогичным образом можно получить функции вида 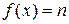для всех значений n, т.е.

.

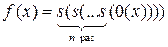Для правильного применения операции суперпозиции функций необходимо соблюдение следующего условия: каждая функция 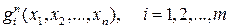должна быть функцией n аргументов.

Задача. Рассмотрим вычисление дискриминанта квадратного трехчлена. Дискриминант 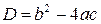квадратного трехчлена 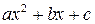можно рассматривать как функцию трех переменных 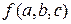. Если в качестве функции h рассмотреть функцию 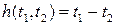, то функцию 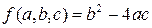можно представить в виде 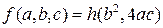. Это означает, что 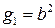, а 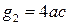. Очевидно, что функция 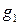есть функция одной переменной, а функция 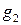является функцией двух переменных. Для корректного применения операции суперпозиции необходимо, чтобы эти функци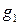и и 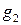были функциями трех переменных 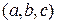. Поэтому в общей записи этих функций необходимо предположить, что они зависят от трех переменных, т.е взять их в виде , .

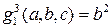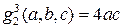2. Оператор примитивной рекурсии. Пусть заданы две примитивно-рекурсивные функци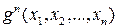и и 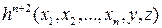, зависящие соответственно от n и n+2 переменных. Оператор примитивной рекурсии позволяет построить новую функцию 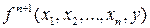от n+1 переменной. Значения новой функции f вычисляем по двум правилам:

,

.

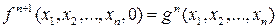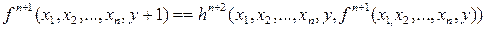Тогда функция 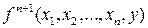получена с помощью оператора примитивной рекурсии и обозначается .

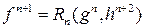Слово «рекурсия» (recurso на латинском языке – возвращаюсь) означает вычисление значения функции 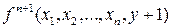с использованием 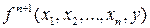(возвращение к ранее вычисленному значению). Это означает, что сначала (при фиксированных значениях 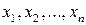) определяется значение функци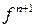и при 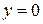, а затем каждое следующее значение функции (зависящее от 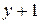) выражается через предыдущее значение (зависящее от ).

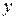Если 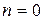, то можно получить функцию одной переменной. В этом случае функция 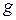имеет ноль переменных и поэтому отождествляется как некоторая постоянная величина а (константа), т.е. 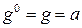. Функция 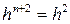зависит от двух переменных. Обозначим ее так: 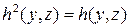. Тогда применяя оператор примитивной рекурсии, получим:

,

.

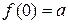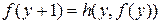Как и в случае оператора суперпозиции, вычислимость исходных функци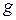й и 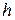влечет вычислимость построенной из них функции .

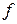Пример 13. Даны функци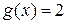и и 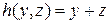. Определить функцию 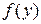, полученную из данных функций по схеме примитивной рекурсии.

Р е ш е н и е.Найдем значения функции .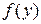

,

;

;

;

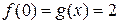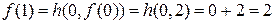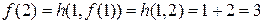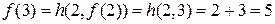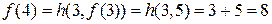и т.д.

Можно предположить, что 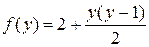, и доказать эту формулу методом математической индукции по переменной .►

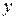Пример 14. Даны функци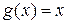и и 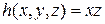. Определить функцию 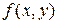, полученную из данных функций по схеме примитивной рекурсии.

Р е ш е н и е. Найдем значения функции :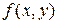

,

;

;

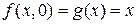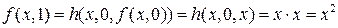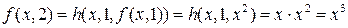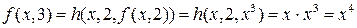и т.д.

Можно предположить, что 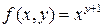, и доказать эту формулу методом математической индукции по переменной . ►

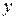Теперь определим примитивно-рекурсивные функции более строго.

Примитивно-рекурсивными функциями называются функции, полученные из простейших примитивно-рекурсивных функций с помощью конечного числа операторов суперпозиции и (или) примитивной рекурсии.

Пример 15. Доказать, что функция 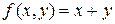примитивно-рекурсивна.

Р е ш е н и е.Функция 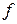является функцией двух переменных. Следовательно, функция 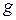должна зависеть от одной переменной, а функция 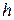– от трех. Пользуясь заданием функции, найдем ее значения:

,

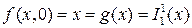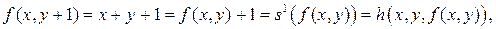т. е.

.

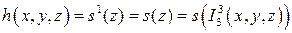Таким образом, функция 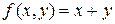получена по схеме примитивной рекурсии ( 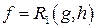) из простейших примитивно-рекурсивных функций, следовательно, сама является примитивно-рекурсивной.►

Пример 16. Доказать, что функция 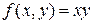примитивно-рекурсивна.

Р е ш е н и е.Функция 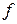является функцией двух переменных. Следовательно, функция 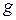должна зависеть от одной переменной, а функция 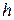– от трех. Пользуясь заданием функции, найдем ее значения:

,

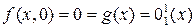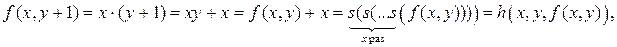
т. е.

.

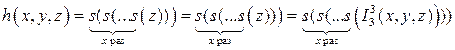Таким образом, функция 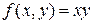получена по схеме примитивной рекурсии ( 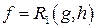) из простейших примитивно-рекурсивных функций, следовательно, сама является примитивно-рекурсивной.

Аналогично, можно показать, что следующие функции также являются примитивно-рекурсивными: , , , , ►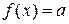

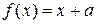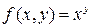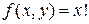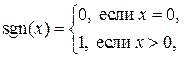
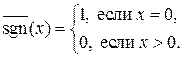3. Операция минимизации. Операция минимизации по 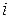-ой переменной функции 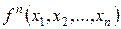обозначается следующим образом: 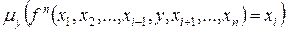, и определяется так.

Рассмотрим уравнение относительно :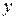

.

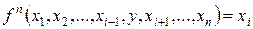Это уравнение решается подбором, вместо переменной 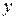последовательно подставляются 0,1,2,… При этом возможны случаи.

· На некотором шаге левая часть соотношения не определена. Следовательно, на наборе 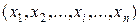операция минимизации не определена.

· На каждом шаге левая часть соотношения определена, но равенство не выполняется ни при каких значениях 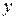. Следовательно, на наборе 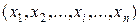операция минимизации не определена.

· Левая часть соотношения определена при 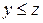, но при 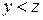равенство не выполняется, а при 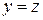выполняется. В этом случае число 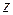считается значением операции минимизации на наборе .

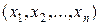Пример 17. Найти функции, получаемые из данной числовой функции 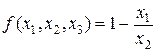с помощью оператора минимизации по каждой ее переменной.

Р е ш е н и е.Минимизируем функцию по переменной 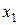. Рассмотрим уравнение .

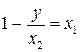1. Если 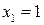, , 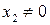то при подстановке 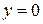в уравнение получаем верное равенство.

2. Если 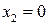, то левая часть уравнения не определена.

3. Если 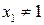, , 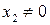то при подстановке 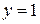в левой части уравнения появляется выражение 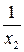, не имеющее смысла, и в этом случае операция минимизации не определена.

Если 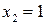, то получаем равенство 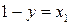. Оно имеет смысл только при 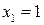, то есть 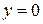, что рассмотрено в первом пункте, и при 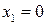, то есть 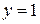. При 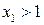равенство не имеет смысла.

Таким образом,

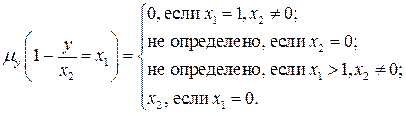
Минимизируем функцию по переменной 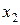. Рассмотрим уравнение 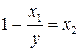. Это уравнение на самом первом шаге, при подстановке вместо 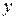нуля теряет смысл, значит, операция минимизации по второй переменной 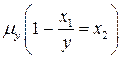нигде не определена.

Минимизируем функцию по переменной 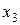. Рассмотрим уравнение 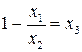. Последнее соотношение должно выполняться при любом значении y. В частности, оно должно иметь смысл и на первом шаге, то есть при 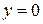. В остальных случаях значение операции минимизации не определено. Таким образом, имеем:

►

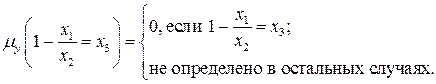Пример 18.Найти функции, получаемые из данной числовой функции 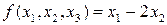с помощью оператора минимизации по каждой ее переменной.

Р е ш е н и е.Минимизируем функцию по переменной 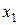. Рассмотрим уравнение 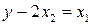. Очевидно, что .

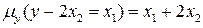Минимизируем функцию по переменной 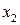. Рассмотрим уравнение 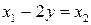. Разрешая последнее уравнение относительно у, получим, что ►

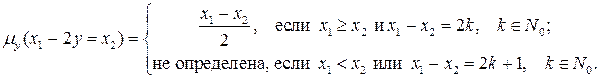Вопросы для самопроверки

1. Понятие множества. Основные понятия (универсальное, счетное и пустое множество). Равные и эквивалентные множества.

2. Операции над множествами: объединение, пересечение, разность дополнение. Диаграммы Венна. Примеры.

3. Понятие кортежа. Прямое (декартово) произведение множеств. Примеры.

4. Бинарное отношение (определение), его область определения и область значений, свойства (рефлексивность, симметричность, транзитивность). Отношения эквивалентности и порядка.

5. Мощности конечных множеств. Принцип включений-выключений. Примеры. Понятие о мощности бесконечных множеств.

6. Определение функции как бинарного отношения. Функция как отображение одного множества на другое. Области определения и значений функции. Примеры.

7. Основные правила комбинаторики (правило суммы и правило произведения). Примеры.

8. Комбинации элементов: размещения, сочетания, перестановки (без повторений). Формулы нахождения числа таких комбинаций. Примеры.

9. Комбинации элементов: размещения, сочетания, перестановки (с повторениями). Формулы нахождения числа таких комбинаций. Примеры.

10. Понятие высказывания. Основные логические операции (связки): отрицание, конъюнкция, дизъюнкция. Их таблицы истинности и взаимосвязь с операциями над множествами.

11. Основные логические операции (связки): импликация, эквивалентность. Их таблицы истинности и запись с помощью дизъюнкций, конъюнкций и отрицаний.

12. Понятие о производных логических операциях (связках): штрих Шеффера, стрелка Пирса, сумма по модулю два. Таблица истинности этих операций.

13. Основные свойства логических операций: идемпотентность, коммутативность, ассоциативность, дистрибутивность, Примеры.

14. Основные свойства логических операций: двойное отрицание, законы де Моргана, поглощение. Примеры.

15. Понятие о булевой алгебре; алгебра высказываний как интерпретация булевой алгебры.

16. Формулы алгебры логики и их виды: тождественно истинные, тождественно ложные и выполнимые. Примеры.

17. Булевы (логические) функции. Равенство функций. Булевы функции одной и двух переменных.

18. Дизъюктивная нормальная форма (ДНФ) и совершенная ДНФ (СДНФ) алгебры логики и их свойства.

19. Конъюнктивная нормальная форма (КНФ) и совершенная КНФ (СКНФ) алгебры логики и их свойства.

20. Построение СДНФ и СКНФ булевой функции по таблице е истинности. Примеры. Теорема о функциональной полноте.

21. Исчисление высказываний. Понятие об алфавите, формулах, аксиомах, правилах вывода и основных теоремах исчисления высказываний.

22. Понятие предиката (высказывательной формы). Предметные переменные. Одноместные и 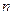-местные предикаты. Тождественно истинные и тождественно ложные высказывания. Примеры.

23. Операции квантор общности и квантор существования. Примеры. Свободные и связанные переменные. Выполнимые и противоречивые формулы логики предикатов.

24. Равносильные формулы логики предикатов. Примеры. Понятие об исчислении предикатов.

25. Неориентированные графы. Основные понятия: вершины и их степень, ребра, кратные ребра, петли. Матрица смежности неориентированного графа. Примеры.

26. Инцидентность. Матрица инцидентности неориентированного графа. Примеры.

27. Ориентированные графы. Матрица инцидентности орграфа. Примеры.

28. Матрица смежности орграфа. Примеры.

29. Подграфы. Полные графы. Клики. Примеры.

30. Операции над графами: дополнение, объединение и пересечение. Примеры.

31. Маршруты, циклы, цепи в неориентированных графах. Связность.

32. Деревья и их свойства. Направленные деревья.

33. Остовное дерево. Цикломатическое число. Остовное дерево минимальной нагруженности.

34. Двудольные графы. Задача о паросочетаниях.

35. Понятие алгоритма. Основные требования к алгоритмам.

36. Понятие рекурсии. Рекурсивные функции. Связь между алгоритмами и рекурсивными функциями.

37. Операции образования примитивно и частично рекурсивных функций. Тезис Чёрча.

38. Простейшие примитивно-рекурсивные функции.

39. Операция суперпозиции (для построения примитивно рекурсивной функции). Пример.

40. Операция примитивной рекурсии. Пример.

41. Операция минимизации (для построения частично рекурсивных функций). Пример.