Метод северо - западного угла

Рассмотрим "северо-западный угол" незаполненной таблицы, то

есть клетку, соответствующую первому поставщику и первому потребителю.

Возможны три случая.

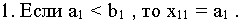
Это означает, что первый поставщик отгрузил весь произведенный продукт первому потребителю и его

запас равен нулю, поэтому

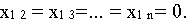
При этом неудовлетворенный спрос в первом пункте потребления равен

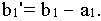
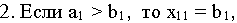
то есть спрос первого потребителя полностью удовлетворен и поэтому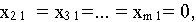

а остаток продукта в первом пункте производства равен

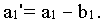
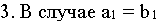
из рассмотрения можно исключить и поставщика, и потребителя. Однако при атом план получается вырожденным,

поэтому условно считается, что выбывает только поставщик,

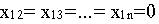
а спрос потребителя остается неудовлетворенным и равным нулю.

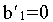
После этого рассматриваем северо-западный угол оставшейся не-

заполненной части таблицы и повторяем те же действия. В результате

через n+m-1 шагов получим опорный план.

Разработка основных алгоритмов решения задачи

1 Алгоритм решения транспортной задачи

1. Проверить выполнение необходимого и достаточного условия разрешимости задачи. Если задача имеет неправильный баланс, то вводится фиктивный поставщик или потребитель с недостающими запасами или запросами и нулевыми стоимостями перевозок.

2. Построить начальное опорное решение (методом северо-западного угла), проверить правильность его построения по количеству занятых клеток (их должно быть m+n-1).

3. Построить систему, соответствующую опорному решению.

4. Проверить выполнения условия оптимальности.

5. Перейти к опорному решению, на котором значение целевой функции будет меньше. Для этого находят клетку таблицы задачи, которой соответствует наибольшая положительная оценка

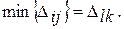
Строят цикл, включающий в свой состав данную клетку и часть клеток, занятых опорным решением. В клетках цикла расставляют поочередно знаки «+» и «-», начиная с «+» в клетке с наибольшей положительной оценкой. Осуществляют сдвиг (перераспределение груза) по циклу на величину 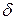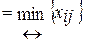. Клетка со знаком «-», в которой достигается 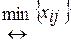остается пустой. Если минимум достигается в нескольких клетках, то одна из них остается пустой, а в остальных проставляют базисные нули, чтобы число занятых клеток оставалось равным .

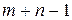Далее перейти к пункту 3 данного алгоритма.

Решение задачи

Открытая модель транспортной задачи:

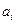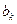У данной транспортной задачи открытая модель и количество спроса превышает количество предложений, вводят фиктивную строку. Получают:

Таблица 1

bk ai
	3	7	1	5	4	9
	7	5	8	6	3	4
	6	4	8	3	2	5
	3	1	7	4	2	3
	0	0	0	0	0	0

Составляют транспортную таблицу.

Таблица 2

bk ai
	3 10	7	1	5	4	9
	7	5	8	6	3	4
	6	4	8	3	2	5
	3	1	7	4	2	3
	0	0	0	0	0	0

В первую клетку помещают: Х₁₁=min(30,10)=10.Спрос первого потребителя полностью удовлетворён, первый столбец вычеркивают. Остаток сырья в первом пункте составляет:30-10=20 усл. ед. Двигаемся по первой строке вправо Х₁₂=min(30-10,35)=20.Предложение первого поставщика исчерпано, первая строка вычеркивается. Второму потребителю не хватает 35-20=15 усл. ед. Двигаемся по второму столбцу в низ Х₂₂=min(5,35)=5. Предложение второго поставщика исчерпано, вторая строка вычеркивается. Второму потребителю не хватает 35-25=10 усл. ед. Двигаемся по второму столбцу в низ Х₃₂=min(45,35-25)=10.Спрос потребителя исчерпан. Двигаемся по третьей строчке вправо Х₃₃=min(45,15-0)=15. Спрос третьего потребителя исчерпан. Двигаемся по третьей строчке вправо Х₃₄=min(45-25,25)=20. Предложения третьего поставщика исчерпаны, третья строка вычеркивается. Четвертому потребителю не хватает 25-20=5 усл. ед. Двигаемся по четвертому столбцу в низ Х₄₄=min(45,25-20)=5. Спрос четвертого поставщика исчерпан. Двигаемся по четвертой строчке вправо Х₄₅=min(40-5,55)=35. Предложения четвертого поставщика исчерпано. Двигаемся по пятому столбцу в низ 55-35=20 усл. ед. Х₅₅=min(30,55-35)=20. Спрос пятого потребителя исчерпан. Двигаемся по пятой строчке вправо Х₅₆=min(30-20, 10)=10. Таблица заполнена. Число нулевых значений Х_{i j} , i=1,5; j=1,6, равно 10. Число базисных переменных задачи 5+6-1=10. Остальные 5*6-10=20 переменных являются свободными, их значения равны нулю.

Таблица 3

bj ai
	3	7	1	5	4	9
	7	5	8	6	3	4
	6	4	8	3	2	5
	3	1	7	4	2	3
	0	0	0	0	0	0
	-3	-7	-11	-6	-4	-4

Таблица 4

bj ai
	0	0 -	-10 +	-1	0	5
	6	0	-1	2	1	2
	6	0 +	0 -	0	1	4
	2	-4	-2	0	0	1
	1	-3	-7	-2	0	0

Таблица 5

bj ai
	0	0	-10	-1	0	5
	6	0	-1	2	1	2
	6	0	0	0	1	4
	2	-4	-2	0	0	1
	1	-3	-7	-2	0	0
	-10	-10		-10	-10	-10

Таблица 6

bj ai
	0	0	0	-1	0	5
	6	0	9	2	1	2
	6	0 -	10	0 +	1	4
	2	-4 +	8	0 -	0	1
	1	-3	3	-2	0	0

Таблица 7

bj ai
	0	0	0	-1	0	5
	6	0	9	2	1	2
	6	0	10	0	1	4
	2	-4	8	0	0	1
	1	-3	3	-2	0	0
					-4	-4

Таблица 8

bj ai
	0	0 -	0	-1	-4 +	1
	6	0	9	2	-3	-2
	6	0	10	0	-3	0
	6	0 +	12	4	0 -	1
	5	1	7	2	0	0

Таблица 9

bj ai
	0	0	0	-1	-4	1
	6	0	9	2	-3	-2
	6	0	10	0	-3	0
	6	0	12	4	0	1
	5	1	7	2	0	0
	-4		-4

Таблица 10

bj ai
	0	4	0	3	0	5
	2	0 -	5	2	-3 +	-2
	2	0	6	0	-3	0
	2	0 +	8	4	0 -	1
	1	1	3	2	0	0

Таблица 11

bj ai
	0	4	0	3	0	5
	2	0	5	2	-3	-2
	2	0	6	0	-3	0
	2	0	8	4	0	1
	1	1	7	2	0	0

Таблица 12

bj ai
	0	4	0	3	0	5
	5	3	8	5	0	1
	2	0 -	6	0	-3 +	0
	2	0 +	8	4	0 -	1
	1	1	7	2	0	0

Таблица 13

bj ai
	0	4	0	3	0	5
	5	3	8	5	0	1
	2	0	6	0	-3	0
	2	0	8	4	0	1
	1	1	7	2	0	0
				-3

Таблица 14

bj ai
	0	0	0	0	0	5
	5	3	8	2	0	1
	5	3	9	0 -	0 +	3
	0	0	8	1	0	1
	1	1	7	-1 +	0 -	0

Таблица 15

bj ai
	0	0	0	0	0	5
	5	3	8	2	0	1
	5	3	9	0	0	3
	0	0	8	1	0	1
	1	1	7	-1	0	0
						-1

Таблица 16

bj ai
	0	0	0	0	0	4
	5	3	8	2	0	0
	5	3	9	0	0	2
	0	0	8	1	0	0
	2	2	8	0	1	0

f = 10*3+15+5*4+5*3+3*5+40*2+5*2+35=30+15+20+15+15+80+10=220.

Заключение

Открытая модель транспортной задачи, играет не малую роль в экономики. Решение этих задач требуется, когда необходимо спланировать поставки сырья, или построить план распределения имеющихся ресурсов.

В результате данной работы были достигнуты поставленные цели и задачи, а именно:

1. изучен теоретический материал и методы решения задач по теме: «Открытая модель транспортной задачи»;

2. разработан алгоритм решения задачи данного типа;

3. Пока созданная программа не предназначена для решения открытой модели транспортной задачи, и нуждается в доработке.

В будущем можно реализовать программу для решения задачи данного типа с разным количеством поставщиков и потребителей.

Список литературы

1 Сборник задач и упражнений по высшей математике: математическое программирование: учебник пособие / А.В. Кузнецов, В.А. Сакович, Н.И. Холод и др; МН.: выш. ик., 2002. – 447с.:ил.

2 Т.Л. Партыкина, И.И. Попов Математические методы: учебник. – М.: ФОРУМ: ИНФА-М, 2005. – 464 с.: ил – (профессиональное образование)

3 И.Г. Семакин Основы программирования: учебник для сред. проф. Образования / И.Г. Семакин, А.П.Шестаков. – 2-е изд., стер,- М.: Издательский центр «Академия», 2003.-432 с.

4 Федосеев В.В. и др. Экономико-математические методы и прикладные модели: учебное пособие для ВУЗов. - М.: Юнити, 2002.