Характеристики в плоскости годографа скорости
Определим изменение скорости вдоль характеристик в физической плоскости и плоскости годографа (рис. 5.4). Пусть в физической плоскости для некоторой точки А (рис. 5.4, а) известны значение и направление скорости потока 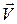 .
.
|
|

Рис. 5.4. Характеристики:
а – в физической плоскости; б – в плоскости годографа
Тогда в плоскости годографа скорости (  ) точке А будет соответствовать точка
) точке А будет соответствовать точка  (рис. 5.4, б). При перемещении вдоль характеристики первого семейства в плоскости XОY концы векторов скорости в плоскости
(рис. 5.4, б). При перемещении вдоль характеристики первого семейства в плоскости XОY концы векторов скорости в плоскости  опишут кривую
опишут кривую  , а для характеристики второго семейства – кривую
, а для характеристики второго семейства – кривую  Характеристики в плоскости
Характеристики в плоскости  располагаются в области, ограниченной двумя окружностями, описанными из начала координат, радиусами
располагаются в области, ограниченной двумя окружностями, описанными из начала координат, радиусами  и
и  и определяющими границы диапазона сверхзвуковых скоростей.
и определяющими границы диапазона сверхзвуковых скоростей.
Чтобы найти уравнение характеристик в плоскости годографа скорости воспользуемся уравнением (5.4), которому должны удовлетворять составляющие скорости  сверхзвукового потока газа.
сверхзвукового потока газа.
Рассматривая изменение скорости вдоль характеристик y = y(x) запишем очевидные соотношения:
 (5.13)
(5.13)
где  – тангенс угла наклона касательной к характеристике в плоскости XY. Тогда из соотношений (5.13) имеем следующее:
– тангенс угла наклона касательной к характеристике в плоскости XY. Тогда из соотношений (5.13) имеем следующее:
 ,
,  . (5.14)
. (5.14)
Из условия потенциальности течения следует, что  . После подстановки уравнения (5.14) в выражение (5.4) с учетом потенциальности получаем
. После подстановки уравнения (5.14) в выражение (5.4) с учетом потенциальности получаем
 ×
×
×  . (5.15)
. (5.15)
Используя свойство корней квадратного уравнения (теорему Виета) для характеристик в плоскости потока
 и
и  ,
,
можно убедиться, что множитель перед  равен
равен 
Вдоль характеристик первого семейства в физической плоскости, когда  , этот множитель равен
, этот множитель равен  , а вдоль характеристик второго семейства, когда
, а вдоль характеристик второго семейства, когда  , он равен
, он равен  . В общем случае для характеристик обоих семейств этот множитель равен
. В общем случае для характеристик обоих семейств этот множитель равен
 .
.
Таким образом, в уравнении (5.15) выражение в квадратных скобках перепишется в виде  . Произведя дальнейшие преобразования уравнения (5.15) с использованием выражений для корней квадратного уравнения, найдем отношение приращений скоростей
. Произведя дальнейшие преобразования уравнения (5.15) с использованием выражений для корней квадратного уравнения, найдем отношение приращений скоростей  вдоль характеристик:
вдоль характеристик:

 .
.
Анализ полученного выражения показывает, что для характеристик первого семейства, где 
 , а для второго семейства (
, а для второго семейства (  ) –
) –  . Таким образом, получаем зависимости для расчета изменения скорости течения газа вдоль характеристик в плоскости потока, которые имеют вид
. Таким образом, получаем зависимости для расчета изменения скорости течения газа вдоль характеристик в плоскости потока, которые имеют вид
 (5.16)
(5.16)
Зависимости (5.16) показывают, что характеристики в физической плоскости и в плоскости годографа скорости перпендикулярны друг другу. Характеристики первого семейства в плоскости XY перпендикулярны характеристикам второго семейства в плоскости  и наоборот. Используя дифференциальное уравнение (5.12) для характеристик в плоскости потока, можно записать следующее:
и наоборот. Используя дифференциальное уравнение (5.12) для характеристик в плоскости потока, можно записать следующее:
 . (5.17)
. (5.17)
Вдоль характеристик в физической плоскости составляющие вектора скорости потока удовлетворяют обыкновенному дифференциальному уравнению в переменных  . Поэтому для любых безвихревых течений газа характеристики в плоскости годографа скорости имеют всегда один и тот же вид и могут быть заранее рассчитаны (в физической плоскости XY характеристики для различных задач различны).
. Поэтому для любых безвихревых течений газа характеристики в плоскости годографа скорости имеют всегда один и тот же вид и могут быть заранее рассчитаны (в физической плоскости XY характеристики для различных задач различны).
Примечание: правая часть уравнения (5.17) не зависит от переменных x, y.
Получим уравнение характеристик в плоскости годографа в интегральном виде. Используя рис. 5.3, можно получить
 ,
,  ,
,
или
 . (5.18)
. (5.18)
Произведем замену 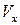 и
и 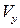 через
через 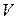 и
и  . Так как
. Так как  и
и  , то
, то  ,
,  , и уравнение (5.18) после преобразований запишем следующим образом:
, и уравнение (5.18) после преобразований запишем следующим образом:
 .
.
|
 равна
равна  , поэтому
, поэтому  . Представив скорость звука как
. Представив скорость звука как  , имеем следующее:
, имеем следующее:  .
.
После интегрирования, учитывая, что  получим уравнение характеристик в плоскости годографа скорости в конечном виде:
получим уравнение характеристик в плоскости годографа скорости в конечном виде:
 . (5.19)
. (5.19)
В этом уравнении число Маха может изменяться в пределах  , что соответствует изменению скорости от
, что соответствует изменению скорости от  до
до  .
.
Кривые, описываемые этим уравнением, называются эпициклоидами. Через каждую точку плоскости  проходит одна эпициклоида первого семейства и одна второго семейства. Задавая различные значения постоянной C, можно один раз вычертить сетку характеристик в плоскости годографа скорости и затем использовать ее при решении задач различного плана.
проходит одна эпициклоида первого семейства и одна второго семейства. Задавая различные значения постоянной C, можно один раз вычертить сетку характеристик в плоскости годографа скорости и затем использовать ее при решении задач различного плана.
Таким образом, с помощью метода характеристик можно решать любые краевые задачи для сверхзвуковых потенциальных течений газа, если только найдены характеристики в плоскости XY течения газа и установлено их соответствие характеристикам в плоскости годографа  . Таким образом, существо решения газодинамических задач методом характеристик состоит в поиске характеристик в плоскости течения газа.
. Таким образом, существо решения газодинамических задач методом характеристик состоит в поиске характеристик в плоскости течения газа.
